
- •Лекция №3
- •Синтаксис логики высказываний
- •Семантика логики высказываний
- •Семантика логики высказываний
- •Логический вывод и логическое следствие
- •Проверка по моделям
- •Хорновские базы знаний
- •Почему хорновские базы знаний получили широкое распространение?
- •Почему хорновские базы знаний получили широкое распространение?
- •Почему хорновские базы знаний получили широкое распространение?
- •Алгоритмы прямого и обратного
- •Алгоритм прямого логического вывода
- •Алгоритм прямого логического вывода:
- •Алгоритм прямого логического вывода:
- •Алгоритм прямого логического вывода:
- •Алгоритм прямого логического вывода:
- •Алгоритм прямого логического вывода:
- •Алгоритм прямого логического вывода:
- •Алгоритм прямого логического вывода:
- •Алгоритм прямого логического вывода:
- •Алгоритм прямого логического вывода:
- •Алгоритм обратного логического вывода
- •Алгоритм обратного логического вывода:
- •Алгоритм обратного логического вывода:
- •Алгоритм обратного логического вывода:
- •Алгоритм обратного логического вывода:
- •Алгоритм обратного логического вывода:
- •Алгоритм обратного логического вывода:
- •Алгоритм обратного логического вывода:
- •Алгоритм обратного логического вывода:
- •Алгоритм обратного логического вывода:
- •Алгоритм обратного логического вывода:
- •Алгоритм обратного логического вывода:
- •Логика предикатов против логики высказываний
- •Логическое программирование базируется на логике предикатов
- •Синтаксис и семантика логической программы
- •Синтаксис и семантика логической программы
- •Синтаксис и семантика логической программы
- •Примеры предложений логической программы
- •Унификация
- •Унификация
- •Унификация
- •Унификация
- •Унификация
- •Унификация
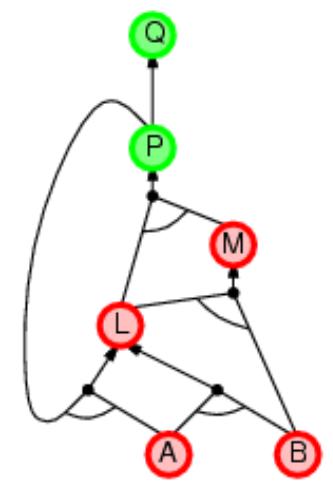
Алгоритм обратного логического вывода:
пример
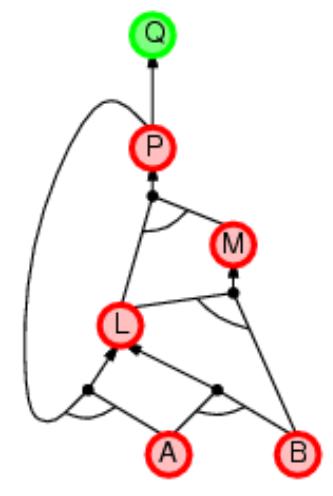
Алгоритм обратного логического вывода:
пример
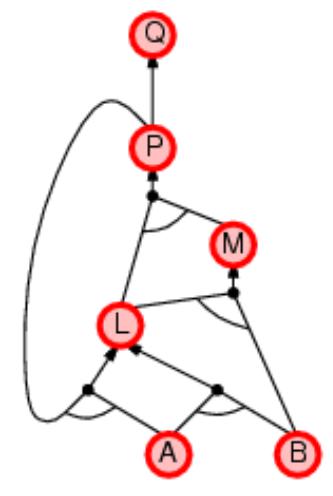
Алгоритм обратного логического вывода:
пример
Логика предикатов против логики высказываний
•Логика высказываний предполагает, что мир состоит из фактов;
•Логика предикатов (как и естественный язык) предполагает, что мир содержит:
–Объекты: люди, дома, числа, цвета, мячи, …
–Отношения: являться красным, круглым, быть братом, больше чем, лежит между, является частью, принадлежит, …
–Функции: отец, лучший друг, плюс, …
Логическое программирование базируется на логике предикатов
Синтаксис и семантика логической программы
Логическая программа представляет собой базу знаний, состоящую из предложений.
Каждое предложение имеет синтаксис A :- B1, B2, … , Bn.
где A, B1, B2, … , Bn – предикаты.
Декларативный (логический) смысл предложения:
B1, B2, … , Bn A
Синтаксис и семантика логической программы
Предикат – это выражение вида pred (term1,...,termm)
где pred – имя предиката (предикатный символ),
term1,...,termm - термы.
Декларативный смысл предиката и термов:
предикат задает отношение между
объектами, задаваемыми термами term1,...,termm .
Синтаксис и семантика логической программы
Терм – это константа, переменная или составной терм.
Константа – число или атом.
Атом – цепочка символов, начинается с маленькой буквы. Указывает на конкретный объект.
Переменная – цепочка символов, начинается с большой буквы. Указывает на неопределенный объект.
Составной терм – выражение вида: func (term1,...,termm)
где func – имя функции (функциональный символ),
term1,...,termm - термы. Позволяет реализовать понятие функции.
Примеры предложений логической программы
отец(олег,семен). мать(мария, семен).
родитель (X,Y):- отец(X,Y); мать(X,Y). родитель (мария,семен). родители(X,Y,Z):- отец(X, Z), мать(Y,Z).
прародитель(X,Y):- родитель(X,Z), родитель(Z,Y).
предок(X,Y):- родитель(X,Y). предок(X,Y):- родитель(X,Z),предок(Z,Y).
любит(X,поклонник(X)):- звезда(X).
Унификация
Унификация позволяет отождествлять формулы логики предикатов путем замены свободных переменных на термы.
Подстановкой называется множество пар вида={x1/t1, x2/t 2 ,…, xn/t n}, где i t i - терм, xi - переменная, не входящая в терм t i , причем xi xj для любых i j. Подстановка может применяться к терму, атомарной формуле, высказыванию или к их множеству. Результат применения подстановки к выражению обозначается Subst( , ) (или ) и называется примером выражения. Пример получается путем одновременной замены каждой переменной xi из на терм ti .
