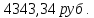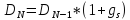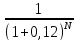Задание 5

Оцените текущую стоимость облигации номиналом 25 000 руб., купонной ставкой 6% годовых и сроком погашения через 9 лет, если рыночная норма прибыли равна 9%.

Решение:

Облигация — единичное долговое обязательство эмитента на возврат номинальной стоимости через определенный срок в будущем, на условиях, устраивающих его держателя. Облигация удостоверяет право кредитора получить и обязательство заемщика выплатить в определенный срок номинальную стоимость облигации и проценты по ней.

Виды облигация по форме выплаты процентного дохода: купонные (процентные) и дисконтные. По первым выплачивается доход в виде определенного процента к ее номиналу, по вторым — весь возможный доход определяется в виде разницы между номиналом облигации и ценой ее приобретения владельцем (последняя в таком случае всегда меньше номинала.

Виды облигаций по виду процентного дохода: с постоянным, фиксированным, плавающим (переменным) или амортизационным доходом. Процентный доход по первым известен заранее (определен условиями эмиссии этой облигации) и не меняется в течение всего срока ее существования. По вторым — уровень процентного дохода заранее известен, но разный в разные купонные периоды. По третьим — уровень дохода меняется по установленным правилам на протяжении времени обращения облигации. По последним — номинал облигации подлежит возврату частями, это указывается при размещении, а купонные платежи выплачиваются к оставшемуся номиналу облигации.

Текущую рыночную стоимость облигации с фиксированным доходом, процентный доход по которым выплачивается в одном и том же размере каждый год (период), можно рассчитать по формуле

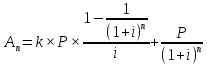
k — купонная процентная ставка

P — номинальная стоимость облигации

i — текущая рыночная процентная ставка (процентная ставка, выплачиваемая на рынке по финансовым инструментам, имеющим ту же степень риска.)

n — оставшийся срок до погашения облигации

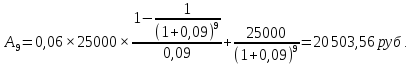
Ответ: текущая рыночная стоимость облигации равна

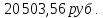
Задание 6

Последний выплаченный дивиденд по акции равен 1 780 руб. Ожидается, что он будет возрастать в течение следующих пяти лет со следующими темпами:

первый год темп составит 12%;

на второй год – 13%;

на третий год – 13%;

на четвертый год – 14%;

на пятый год – 14%.

Затем темп прироста стабилизируется на величине 9%.

Определите, какова теоретическая (текущая) цена акции, если рыночная норма прибыли 12%?

Решение:

Акция — эмиссионная ценная бумага, закрепляющая право ее владельца (акционера) на получение части прибыли акционерного общества в виде дивидендов, на участие в управлении акционерным обществом и на часть имущества, остающегося после его ликвидации. Обыкновенная акция — ценная бумага, эмитируемая акционерным обществом, дающая право на получение нефиксированных дивидендов в случае соответствующих решений Собрания акционеров и в огромном большинстве случаев Совета директоров (Наблюдательного совета). Получение доходов по обыкновенным акциям связано с неопределенностью информации относительно будущих результатов, прежде всего темпов роста дивидендов. Для инвестора единственным источником информации о деятельности фирмы являются ее статистические данные в прошлом.

В данном случае темпы роста акции не постоянные, они начала увеличиваются, а затем уменьшаются. Поэтому будем использовать модель двухстадийного роста (сверхнормальный и нормальный темпы) и считать её текущую цену по формуле

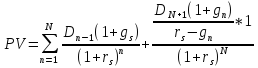
фактические дивиденды за прошедший год

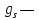сверхнормальный темп роста

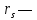требуемая ставка доходности при увеличении темпа роста дивидендов

N — число лет сверхнормального роста

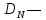дивиденды года N

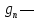нормативный темп роста

Сначала рассчитывается текущая стоимость дивидендов за период сверхнормативного роста, представленная первым слагаемым (таблица 5).

Таблица 5 —Текущая стоимость дивидендов за период сверхнормативного роста

Конец года N	Размер дивиденда, руб.	Фактор дисконтирования (12%)	Текущая стоимость дивидендов
1	100 * 1,12 = 112	0,892857	112*0,892857 = 100
2	112 * 1,13 = 126,56	0,797194	126,56*0,797194=100,89
3	126,56 * 1,13 = 143,01	0,711780	101,79
4	143,01 * 1,14 = 163,03	0,635518	103,61
5	163,03 * 1,14 = 185,85	0,567427	105,46
Итого:				511,76

Определим стоимость акции в конце пятого года (первый множитель второго слагаемого):

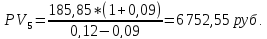
Определим текущую стоимость перепродажи акции (полностью второе слагаемое):

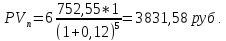
Определим текущую стоимость акции:

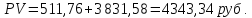
Ответ: теоретическая текущая цена акции равна