Распространение данного материала разрешено при условии сохранения копирайта







~

Праваячасть

f(x)



~



~

~



y



~

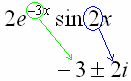
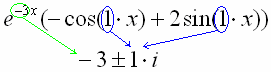
Данная таблица является неотъемлемой частью урока http://mathprofi.ru/kak_reshit_neodnorodnoe_uravnenie_vtorogo_poryadka.html Автор: Емелин А.

V. Характеристическое уравнение имеет сопряженные, чисто мнимые комплексные корни: _1,2 i

В таком диффуре отсутствует первая производная.

_{Пример: Рассмотрим неоднородное уравнение y}_{4y f (x) .}

_{Для соответствующего однородного уравнения y}_{4y 0 составим характеристическое}

уравнение ² 4 0 и найдем его корни: _1,2 2i

Получены чисто мнимые сопряженные комплексные корни:







y

~

~

~

~

~

~

~

Правая часть f (x)

В каком виде нужно искать частное решение ^~

Неоднородного уравнения?

Подбор частного решения осуществляется очевидным «штатным» образом, за исключением следующих видов правой части:

Коэффициент не совпадает с коэффициентом при

31. f (x) sin x _{характеристических сопряженных комплексных корнях ,} поэтому частное решение ищем в обычном виде:

y Acosx Bsin x

Коэффициент совпал с коэффициентом при

характеристических сопряженных комплексных корнях , 32. f (x) 3sin2x _{поэтому при подборе «штатное» частное решение необходимо}

домножить на «икс»: y x(Acos2x Bsin2x), то есть искать

частное решение в виде: y Axcos2x Bxsin2x

Коэффициенты не совпадают с коэффициентом при характеристических сопряженных

33. f (x) 2cos3x 2sin3x _{комплексных корнях , поэтому частное решение ищем в} обычном виде:

y Acos3x Bsin3x

Коэффициенты совпали с коэффициентом при характеристических сопряженных

34. f (x) 2xcos2x sin2x ^{комплексных корнях , поэтому при подборе очевидное} частное решение опять же домножаем на «икс»:

y x((Ax B)cos2x (Cx D)sin2x), или:

y (Ax² Bx)cos2x (Cx² Dx)sin2x

Коэффициент не совпадает с коэффициентом 35. f (x) 3xcos4x ^{при характеристических сопряженных комплексных корнях}

, поэтому частное решение ищем в «штатном» виде: y (Ax B)cos4x (Cx D)sin4x

© http://mathprofi.ru, Высшая математика – просто и доступно!

Распространение данного материала разрешено при условии сохранения копирайта

Данная таблица является неотъемлемой частью урока http://mathprofi.ru/kak_reshit_neodnorodnoe_uravnenie_vtorogo_poryadka.html Автор: Емелин А.

Краткие итоги по 5-ти разделам:





Тип корней характеристического уравнения

Когда следует проявить ПОВЫШЕННОЕ ВНИМАНИЕ при подборе частного решения

I. Характеристическое уравнение

имеет два различных ^{Если в правой части f (x) находится экспонента или}

действительных корня, отличных от нуля

II. Характеристическое уравнение имеет два различных действительных корня,

один из которых равен нулю

III. Характеристическое уравнение имеет два кратных действительных корня

IV. Характеристическое уравнение имеет сопряженные комплексные корни: _1,2 i ,

причём 0, 0

V. Характеристическое уравнение имеет сопряженные,

чисто мнимые комплексные корни: _1,2 i

экспонента, умноженная на многочлен (примеры 5-8)

Если в правой части f (x) находится константа, многочлен,

экспонента или экспонента, умноженная на многочлен (примеры 18-23)

Если в правой части f (x) находится экспонента или экспонента, умноженная на многочлен (примеры 24-26)

Если в уравнении есть правые части, разобранные в примерах 27-30: f (x) 2e^3x sin2x, f (x) 2e^3x cosx ,

f (x) e^x (5cosx 3sin x) и т.п.

Когда в правой части находится синус, косинус или синус и косинус одновременно; либо данные функции, умноженные на многочлены (многочлен) (примеры 31-35)

© http://mathprofi.ru, Высшая математика – просто и доступно!

Распространение данного материала разрешено при условии сохранения копирайта