Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Криворожский национальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3.1-3.180.doc

Скачиваний:

Добавлен:

01.04.2025

Размер:

8.7 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 66

Для визначення струму застосуємо правила Кірхгофа для розгалужених кіл:

1. Алгебраїчна сума всіх сил струмів, що сходяться у вузлі розгалуженого кола, дорівнює нулю:

. (1)

Струми, що входять у вузол, вважають додатними, які виходять — від'ємними, або навпаки.

2. У будь-якому простому замкненому контурі, довільно обраному у розгалуженому електричному колі, алгебраїчна сума добутків сил струмів на опори відповідних ділянок цього контуру дорівнює алгебраїчній сумі електрорушійних сил, що діють у ньому

. (2)

Для вузла та для замкнених контурів і запишемо правила Кірхгофа:

(3)

З другого та третього рівнянь системи (3) знаходимо шуканий струм

, (4)

Підставляємо в рівняння (4) данні умови задачі і отримаємо відповідь:

3.163. Батареї живлення мають е.р.с. = 2 В, =3 В. Опори R₁ = 1 кОм, R₂ = 0,5 кОм та R₃ = 0,2 кОм, опір амперметра дорівнює R_A = 0,2 кОм. (див. рис. 3.163). Знайти, що показує амперметр.

3.162

.163.

Розв’язок.

Дано

= 2 В, =3 В

R₁ = 1 кОм, R₂ = 0,5 кОм

R₃ = 0,2 кОм, R_A = 0,2 кОм

= ?

ля визначення струму застосуємо правила Кірхгофа для розгалужених кіл:

1. Алгебраїчна сума всіх сил струмів, що сходяться у вузлі розгалуженого кола, дорівнює нулю:

. (1)

Струми, що входять у вузол, вважають додатними, які виходять — від'ємними, або навпаки.

. (2)

Для вузла та для замкнених контурів і запишемо правила Кірхгофа:

(3)

Рішення для струмів знаходимо за формулами (метод Крамера):

а) , б) , в) , (4)

де детермінанти дорівнюють:

системи ; (5)

невідомого (6)

Тоді струм знайдемо за формулою (4, в) з використанням виразів (5) і (6):

Два елементи з однаковими е.р.с. = =2 В, та внутрішнім опором r₁ = r₂ = 2 Ом замкнені на зовнішній опір 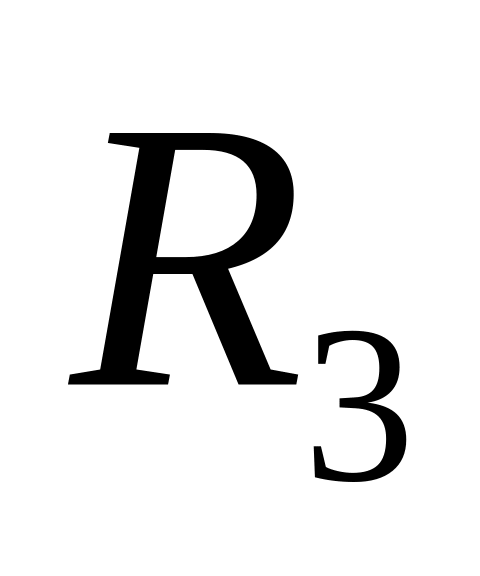(див. рис. 3.164). Через елемент з е.р.с. тече струм I₁ = 1 А. Знайти опір та струм І₂, що тече через елемент з е.р.е. .

3.164.

Розв’язок.

3.164

Дано

= =2 В

r₁ = r₂ = 2 Ом

I₁ = 1 А

= ? = ?

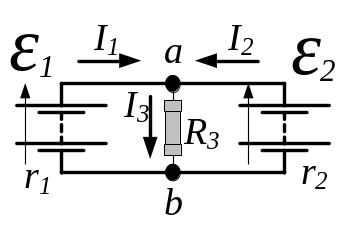
ля визначення струму застосуємо правила Кірхгофа для розгалужених кіл:

1. Алгебраїчна сума всіх сил струмів, що сходяться у вузлі розгалуженого кола, дорівнює нулю:

. (1)

Струми, що входять у вузол, вважають додатними, які виходять — від'ємними, або навпаки.

. (2)

Для вузла та для замкнених контурів і запишемо правила Кірхгофа:

(3)

Рішення для струмів знаходимо за формулами (метод Крамера):

а) , б) , в) , (4)

де детермінанти дорівнюють:

системи ; (5)

невідомого (6)

невідомого (7)

Визначаємо струм , з якого отримаємо невідомий опір :

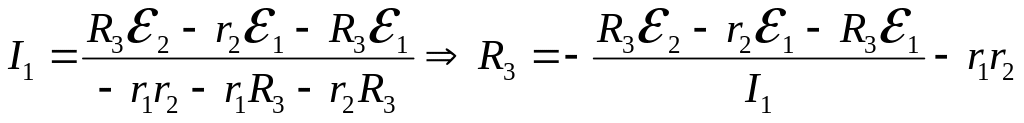. (8)

Тоді струм знайдемо за формулою (4, а) з використанням виразів (5) і (8):

Підставляємо значення величин з умови задачі у формули (8) та (9) і отримуємо відповіді:

= =

3.165. Розв'язати попередню задачу за умови, що = =4 В, r₁ = r₂ = 0,5 Ом, I₁ = 2 A.

3.165.

Розв’язок.

3.165

Дано

= =4 В

r₁ = r₂ = 0,5 Ом

I₁ = 2 А

= ? = ?

ля визначення струму застосуємо правила Кірхгофа для розгалужених кіл:

1. Алгебраїчна сума всіх сил струмів, що сходяться у вузлі розгалуженого кола, дорівнює нулю:

. (1)

Струми, що входять у вузол, вважають додатними, які виходять — від'ємними, або навпаки.

. (2)

Для вузла та для замкнених контурів і запишемо правила Кірхгофа:

(3)

Рішення для струмів знаходимо за формулами (метод Крамера):

а) , б) , в) , (4)

де детермінанти дорівнюють:

системи ; (5)

невідомого (6)

невідомого (7)

Визначаємо струм , з якого отримаємо невідомий опір :

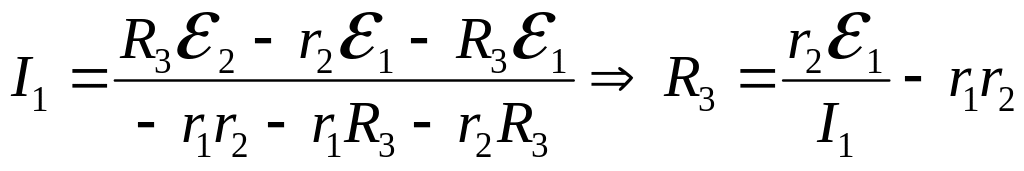. (8)

Тоді струм знайдемо за формулою (4, а) з використанням виразів (5) і (8):

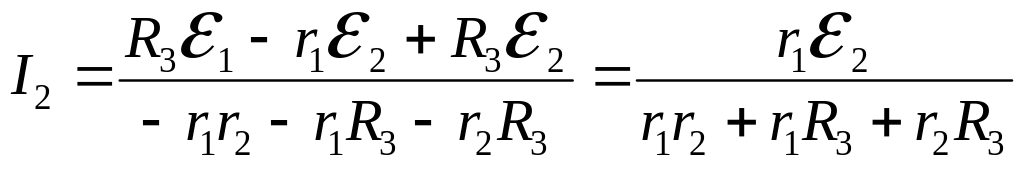
Підставляємо значення величин з умови задачі у формули (8) та (9) і отримуємо відповіді:

= =

3.166. За який час при електролізі водного розчину хлорної міді (СuСl₂) на катоді виділиться = 4,74 грам міді, якщо сила струму дорівнює = 2 А?

3.166.

Дано

= 4,74 г

= 2 А

= 64∙10^-3 кг/моль

= 2

= ?

Розв’язок.

Перший закон Фарадея має вигляд

, (1)

де k - електрохімічний еквівалент.

Другий закон Фарадея

, (2)

де - атомна маса; Кл/моль - число Фарадея; z - валентність речовин.

Електрохімічний еквівалент з формули (2) підставляємо у формулу (1) і визначаємо з отриманого рівняння вираз для розрахунку часу протікання струму через водний розчин хлорної міді:

. (3)

Зробимо підстановку заданих в умові величин у вираз (3) та отримаємо відповідь:

3.167. За який час при електролізі мідного купоросу маса мідного катода збільшиться на = 99 мг? Площа пластинки катода = 25 см², густина струму = 200 А/м² Знайти товщину шару міді, що утвориться на катоді.

3.167.

Дано

= 99 мг

= 25 см²

= 200 А/м²

= 64∙10^-3 кг/моль

= 2

= ? = ?

Розв’язок.

Перший закон Фарадея визначає масу речовини, яка виділиться на одному з електродів за певний час:

, (1)

де k - електрохімічний еквівалент.

Другий закон Фарадея

, (2)

де - атомна маса; Кл/моль - число Фарадея; z - валентність речовин.

Електрохімічний еквівалент з формули (2) підставляємо у формулу (1) і визначаємо з отриманого рівняння вираз для розрахунку часу протікання струму через водний розчин мідного купоросу:

. (3)

Товщина шару міді, що утвориться на катоді дорівнює

, (4)

де = 8600 кг/м³ – густина міді.

Зробимо підстановку заданих в умові величин у вирази (3) та (4) і отримаємо відповіді:

= =

3.168. При електролізі мідного купоросу за одну годину виділилося = 0,5 грам міді. Площа кожного електрода S = 75 см². Знайти густину електричного струму.

3.168.

Дано

= 3600 с

= 0,5 г

= 75 см²

= 64∙10^-3 кг/моль

= 2

= ?

Розв’язок.

Перший закон Фарадея визначає масу речовини, яка виділиться на одному з електродів за певний час:

, (1)

де k - електрохімічний еквівалент.

Другий закон Фарадея

, (2)

де - атомна маса; Кл/моль - число Фарадея; z - валентність речовин.

Електрохімічний еквівалент з формули (2) підставляємо у формулу (1) і визначаємо з отриманого рівняння вираз для розрахунку густину струму через водний розчин мідного купоросу:

. (3)

Зробимо підстановку заданих в умові величин у вираз (3) і отримаємо відповідь:

3.169. Дві електролітичні ванни з розчинами AgNO₂ і CuSO₄ з'єднані послідовно. Яка маса міді виділиться за час, протягом якого виділилось 180 мг срібла?

3.169.

Дано

= 180 мг

= 108∙10^-3 кг/моль

= 64∙10^-3 кг/моль

= 2

= ?

Розв’язок.

Перший закон Фарадея визначає масу речовини, яка виділиться на одному з електродів за певний час:

, (1)

де k - електрохімічний еквівалент.

Другий закон Фарадея

, (2)

де - атомна маса; Кл/моль - число Фарадея; z - валентність речовин.

Електрохімічний еквівалент з формули (2) підставляємо у формулу (1) і складемо систему рівнянь для обох металів:

. (3)

Знаходимо з відношення рівнянь системи (3) вираз для розрахунку Яка маси міді, яка виділиться за заданий час:

(4)

Зробимо підстановку заданих в умові величин у вираз (4) і отримаємо відповідь:

3.170. Яку електричну енергію W треба затратити, щоб при електролізі розчину AgNO₂ виділилось = 500 мг срібла? Різниця потенціалів на електродах = 4 В.

3.170.

Дано

= 500 мг

= 4 В

= 108∙10^-3 кг/моль

= 2

= ?

Розв’язок.

Електричну енергію W струму на ділянці кола знаходимо за формулою:

, (1)

де - час протікання струму, який разом струмом визначаємо з формули законів Фарадея.

Перший закон Фарадея визначає масу речовини, яка виділиться на одному з електродів за певний час:

, (2)

де k - електрохімічний еквівалент.

Другий закон Фарадея

, (3)

де - атомна маса; Кл/моль - число Фарадея; z - валентність речовин.

Електрохімічний еквівалент з формули (2) підставляємо у формулу (1) і визначимо добуток :

. (4)

Отриманий добуток струму на час з виразу (4) підставляємо у формулу (1) і отримаємо для розрахунку енергії:

= (5)

Зробимо підстановку заданих в умові величин у вираз (5) і отримаємо відповідь:

3.171. Площа кожного електрода іонізаційної камери S = 0,01 м², відстань між ними = 6,2 см. Знайти струм насичення І_H в такій камері, якщо в одиниці об'єму в одиницю часу утворюється = 10¹⁵ м^-3с^-1 однозарядних іонів кожного знаку.

3.171.

Дано

S = 0,01 м²

= 6,2 см

= 10¹⁵

= ?

Розв’язок.

При малих густинах струму, який проходить у газі, має місце закон Ома:

, (1)

де - рухливості іонів газу; n - концентрація позитивних і негативних іонів; (кількість пар іонів); = 1,6∙10^-19 Кл – елементарний електричний заряд. Насичення немає. При цьому

, (2)

де - кількість пар іонів, які утворюються під дією іонізатора щосекунди в одиниці об'єму; - коефіцієнт рекомбінації.

Густина і сила струму насичення між плоскими електродами, які знаходяться на відстані d один від одного визначаємо з формули:

. (3)

Зробимо підстановку заданих в умові величин у вираз (3) і отримаємо відповідь:

3.172. Яку найменшу швидкість повинен мати електрон для того, щоб іонізувати атом водню? Потенціал іонізації атома водню дорівнює = 13,5 В.

3.172.

Дано

= 13,5 В

= ?

Розв’язок.

Потенціал іонізації атома водню це енергія електрон, яку він повинен мати, щоб іонізувати атом. Таку енергію електрон може отримати в електричному полі. Тому складемо рівняння закону збереження енергії:

, (1)

де = 9,1∙10^-31 кг – маса електрона; = 1,6∙10^-19 Кл – заряд електрона.

З рівняння (1) отримуємо вираз для розрахунку швидкості:

= (2)

Зробимо підстановку заданих в умові величин у вираз (2) і отримаємо відповідь:

3.173. При якій температурі Т атоми ртуті мають кінетичну енергію поступального руху, достатню для іонізації? Потенціал іонізації атома ртуті = 10,4 В.

3.173.

Дано

= 10,4 В

= ?

Розв’язок.

Середня кінетична енергія одноатомної молекули визначається за формулою

, (1)

де Дж/К - стала Больцмана; — термодинамічна температура газу.

Потенціальна енергія атома в металі дорівнює:

. (2)

Складемо рівняння закону збереження енергії з рівнянь (1) та (2) і визначимо температуру:

, (3)

де = 1,6∙10^-19 Кл – заряд електрона.

Зробимо підстановку заданих в умові величин у вираз (3) і отримаємо відповідь:

3.174. У скільки разів зміниться питома термоелектрона емісія вольфраму, що знаходиться при температурі Т₀ = 2400 К, якщо підвищити температуру вольфраму на ΔT = 100 К?

3.174.

Дано

Т₀ = 2400 К

ΔT = 100 К

= ?

Розв’язок.

Залежність густини струму насичення від температури виражається формулою Річардсона — Дешмана

, (1)

де D - стала, що залежить від властивостей поверхні металу і для чистих металів дорівнює 6,02•10⁵ А/(К²•м²); Дж/К - стала Больцмана; Т — термодинамічна температура катода.

Записуємо рівняння (1) для різних температур металу і визначимо у скільки разів зміниться питома термоелектрона емісія вольфраму:

, (2)

де = 4,54∙1,6∙10^-19 Дж – робота виходу електрона з металу.

Спрощуємо вираз (2), зробимо підстановку заданих в умові величин і отримаємо відповідь:

3.175. Сила струму в провіднику, опором = 10 Ом, змінюється з часом за законом І = І₀ e^-^αt. Знайдіть кількість теплоти, що виділилося в провіднику за час t = 10^-2 с. Прийняти І₀ = 20 A, α = 10² с^-1.

3.175.

Дано

R = 10 Ом

І = І₀ e^-^αt

t = 10^-2 с

І₀ = 20 A,

α = 10² с^-1.

= ?

Розв’язок.

Кількість теплоти , що виділяється в провіднику при проходженні в ньому постійного струму (закон Джоуля — Ленца),

. (1)

З виразу (1) інтегруванням можна отримати вираз для визначення кількості теплоти, що виділиться в провіднику за заданий час:

. (2)

Зробимо підстановку границь інтегрування та заданих в умові величин у вираз (2) та отримаємо відповідь:

3.176. Сила струму у провіднику змінюється з часом за законом І = І₀ sinωt. Знайти заряд , що проходить через поперечний переріз провідника за час рівний половині періоду, якщо початкова сила струму І₀ = 10 А, циклічна частота ω = 50π с^-1

3.176.

Дано

І = І₀ sinωt

І₀ = 10 A,

ω = 50π с^-1

= ?

Розв’язок.

Сила електричного струму чисельно дорівнює зміні заряду, перенесеного через поперечний переріз провідника, залежно від часу

. (1)

Кількість заряду знаходимо інтегруванням виразу (1), розв’язаного відносно елементу заряду:

. (2)

Зробимо підстановку в вираз (2) періоду з формули

, (3)

і отримаємо вираз для розрахунку заряду , що проходить через поперечний переріз провідника за час рівний половині періоду:

= (4)

Підставляємо данні в умові величини у вираз (4) та отримаємо відповідь:

= =

3.177. Сила струму змінюється за законом І = І₀ sinωt. Визначити кількість теплоти, що виділиться в провіднику з опором R = 10 Ом за час від t₁ = 0 до t₂ = T/4. Прийняти Т = 10 с, а І₀ = 20 А.

3.177.

Дано

І = І₀

R = 10 Ом

t₁ = 0

t₂ = T/4

Т = 10 с

І₀ = 20 A

= ?

Розв’язок.

. (1)

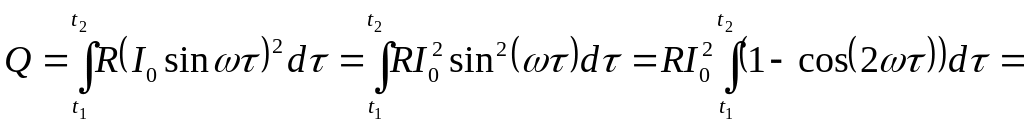
. (2)

Зробимо підстановку границь інтегрування та заданих в умові величин у вираз (2) та отримаємо відповідь:

3.178. Сила струму в провіднику змінюється з часом за законом І = І₀ e^-^αt. Визначити кількість теплоти, що виділиться в провіднику з опором R = 20 Ом за час, протягом якого струм зменшиться в e раз. Прийняти α = 2 10^-2 с^-1, a I₀ = 20 А.

3.178.

Дано

І = І₀ e^-^αt

R = 20 Ом

α = 2 10^-2 с^-1

I₀ = 20 А

= ?

Розв’язок.

. (1)

. (2)

Час знайдемо з умови задачі, тобто за час струм зменшиться в e раз

. (3)

Зробимо підстановку верхньої границі інтегрування з (3) та заданих в умові величин у вираз (2) та отримаємо відповідь:

3.179. При вимиканні джерела живлення сила струму в мережі зменшується за законом І = І₀ e^-^αt (І = 10 А, α = 5∙10² с^-1). Визначити кількість теплоти, що виділиться в резисторі з опором R = 5 Ом після вимикання джерела живлення. Прийняти І₀ = 20 А.

3.179.

Дано

І = І₀ e^-^αt

R = 5 Ом

І = 10 А

α = 5 10^-2 с^-1

I₀ = 20 А

= ?

Розв’язок.

. (1)

. (2)

Час знайдемо з умови задачі, тобто за час струм зменшиться в 2 рази

. (3)

3.180. Сила струму змінюється за законом І = І₀ cosωt. Визначити кількість теплоти, що виділиться в провіднику з опором R = 8 Ом за час від t₁ = 0 до t₂ = Т/4. Прийняти Т = 4 с, а І₀ = 20 А.