
- •Правила Кірхгофа для розгалужених кіл
- •Правила Кірхгофа для розгалужених кіл:
- •Правила Кірхгофа для розгалужених кіл:
- •Правила Кірхгофа для розгалужених кіл мають вигляд:
- •Правила Кірхгофа для розгалужених кіл записуються так:
- •Правила Кірхгофа для розгалужених кіл записуються так:
- •Правила Кірхгофа для розгалужених кіл записуються так:
- •Спочатку замінимо паралельне з’єднання опорів та на еквівалентне згідно з формулою:
- •Правила Кірхгофа для розгалужених кіл записуються так:
- •Спочатку замінимо паралельне з’єднання опорів та на еквівалентне згідно з формулою:
- •Для визначення струму застосуємо правила Кірхгофа для розгалужених кіл:
- •Для визначення струму застосуємо правила Кірхгофа для розгалужених кіл:












3
Рис. 1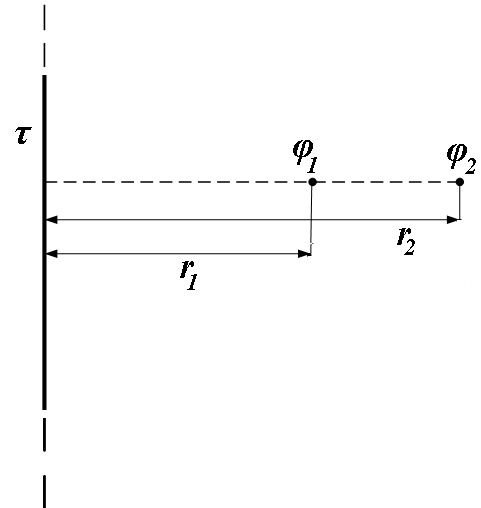
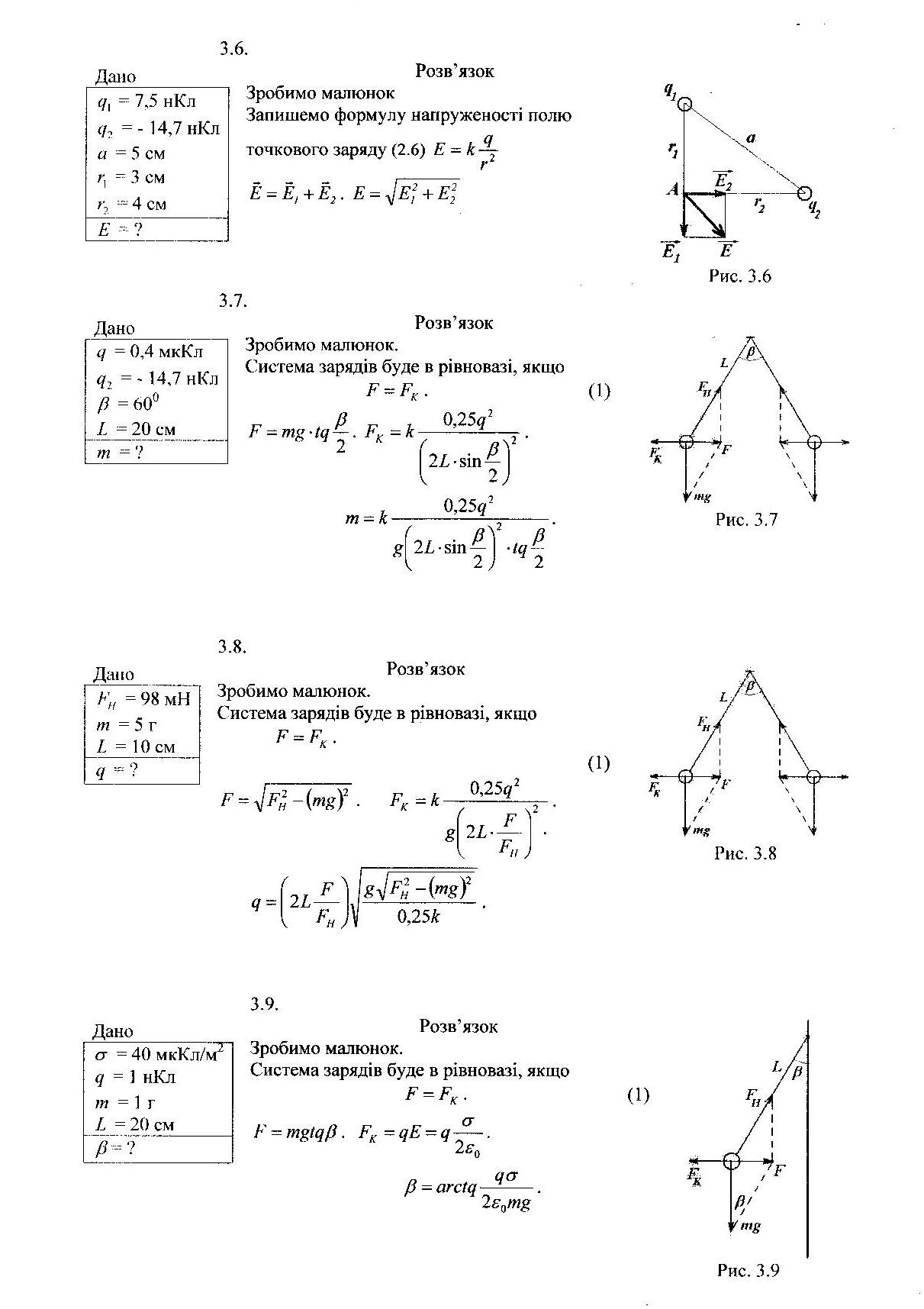
Дано
![]() = 20 пКл/м
= 20 пКл/м![]() = 8 см
= 8 см![]() = 12 см
= 12 см
![]() = ?
= ?
Зробимо малюнок, на якому вертикально зображена нескінченно довга заряджена нитка з лінійною густиною заряду τ.
Різницю потенціалів U двох точок поля, що відстоять від нитки на відстані r1 і r2,
можна визначити
через напруженість
![]() в заданих точках за формулою:
в заданих точках за формулою:
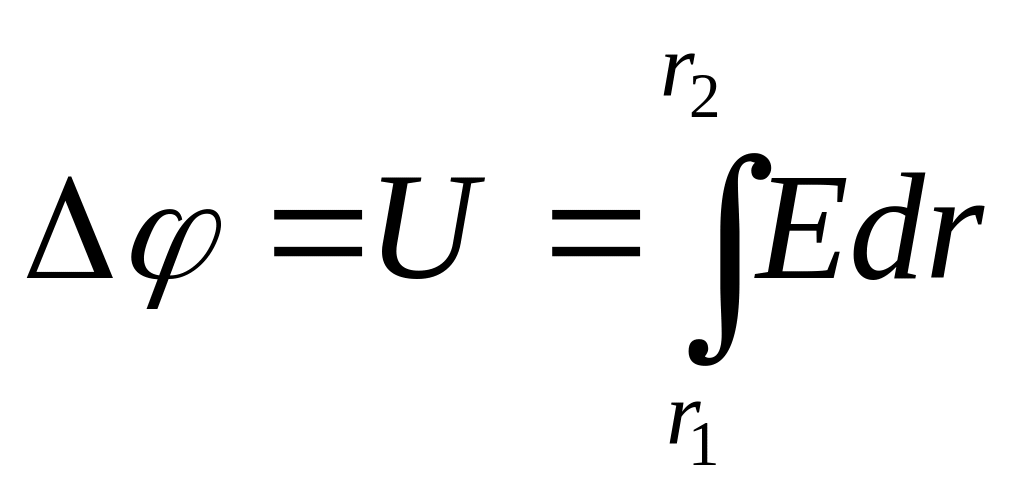 .
.
Напруженість електричного поля утвореного нескінченно довгою зарядженою ниткою визначається за формулою (18.18, в):
![]() ,
,
де
![]() = ………..
= ………..
Якщо виконати інтегрування, отримаємо
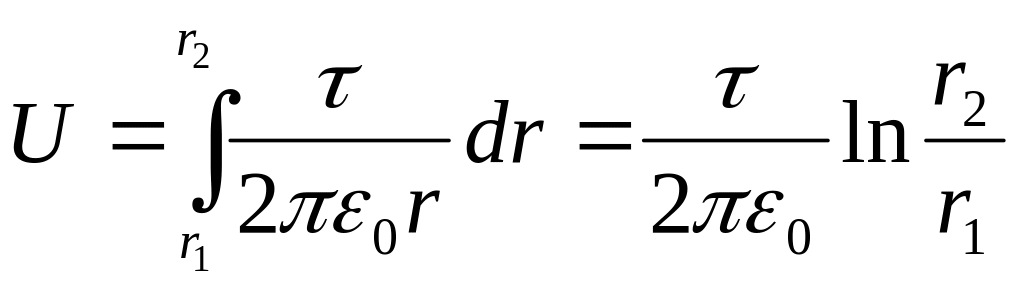 .
.
Зробимо підстановку заданих величин у системі СІ:
=
3

Дано
= 200 пКл/м
![]() = ?
= ?
Зробимо малюнок,
на якому зображений елемент
![]() нижньої сторони рамки, заряд якого можна
вважати точковим. Для точкового заряду
маємо формулу потенціалу поля (18.29).
Застосуємо цю формулу:
нижньої сторони рамки, заряд якого можна
вважати точковим. Для точкового заряду
маємо формулу потенціалу поля (18.29).
Застосуємо цю формулу:
![]() , (1)
, (1)
де
![]() - ……….,
- ……….,
![]() - відстань від точки, в якій визначається
потенціал, до елемента
.
- відстань від точки, в якій визначається
потенціал, до елемента
.
З малюнка видно, що
![]() . (2)
. (2)
Диференціюємо цей вираз
![]() . (3)
. (3)
А відстань визначаємо з трикутника:
![]() . (4)
. (4)
Підставляємо вирази (3) і (4) у вираз (1)
![]() . (5)
. (5)
Інтегруючі вираз
(5) в межах від
![]() до
до
![]() ,
отримаємо потенціал, який створює одна
сторона квадрата
,
отримаємо потенціал, який створює одна
сторона квадрата
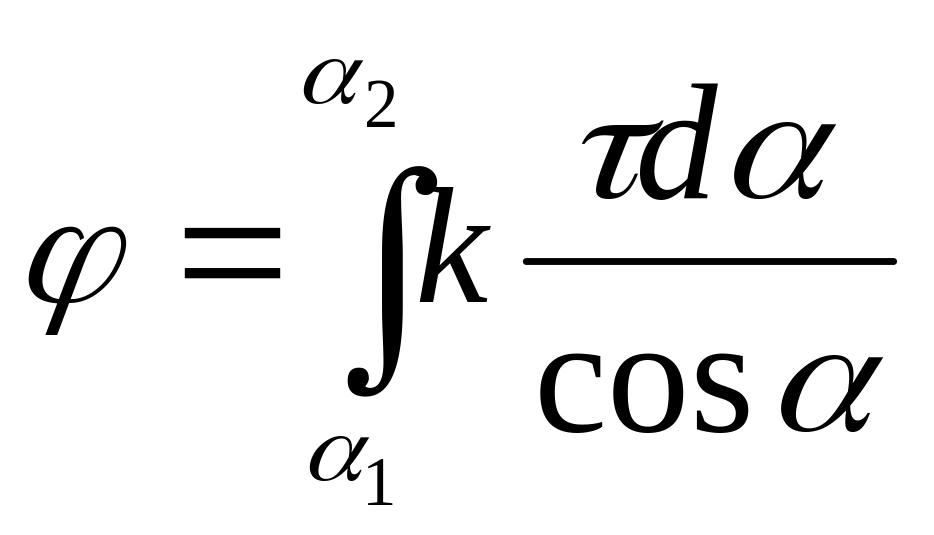 . (6)
. (6)
В силу симетрії
точки
![]() відносно кінців сторони, маємо
відносно кінців сторони, маємо
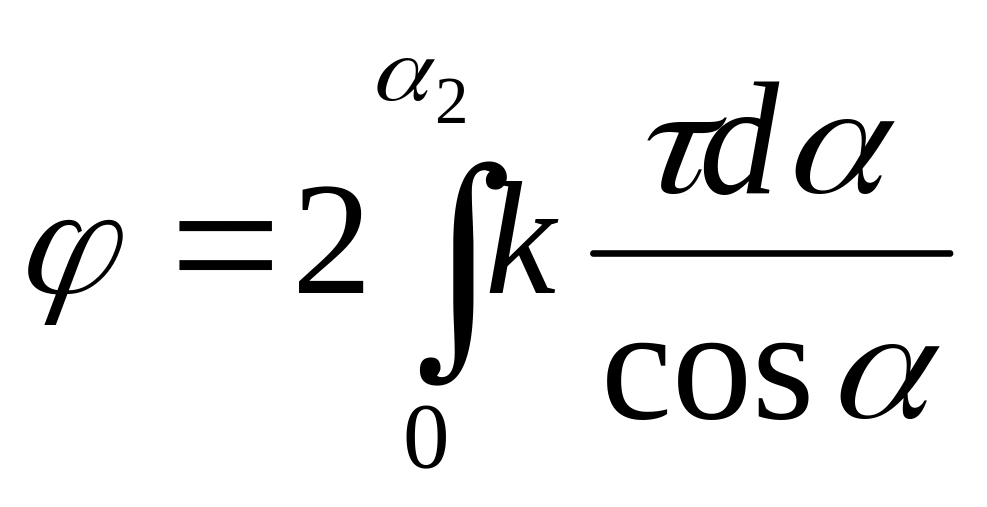 . (7)
. (7)
Так як
![]() .
Див. табл.. 27.
.
Див. табл.. 27.
Тоді для всіх сторін отримаємо
![]() .
.
Підставляємо границі інтегрування і числові значення:
=
Рис. 1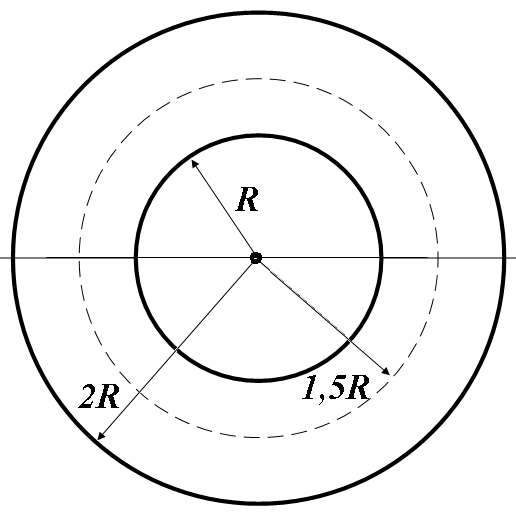
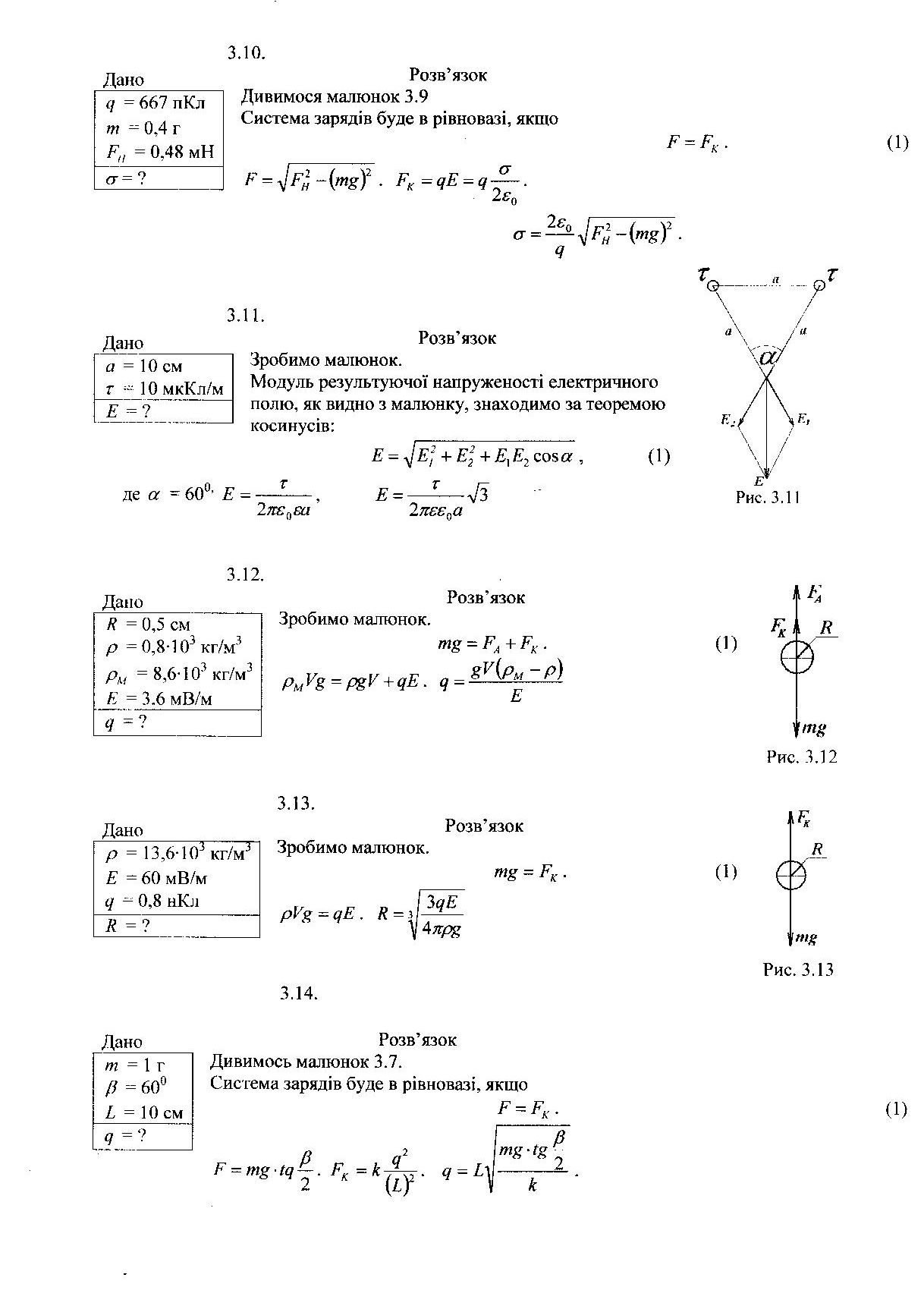
3.53.
Дано
= ?
![]()
![]()
![]()
![]()
![]() = 30 нКл/м2
= 30 нКл/м2![]()
Зробимо малюнок, на якому зображені дві концентричні сфери радіусом R і 2R, по поверхні яких рівномірно розподілені заряди з поверхневою густиною σ1 і σ2.
Застосуємо теорему Гауса до вектора напруженості електричного поля:
1. Для
![]()
![]()
![]() (1)
(1)
2. Для
![]()
 . (2)
. (2)
3. Для
![]()
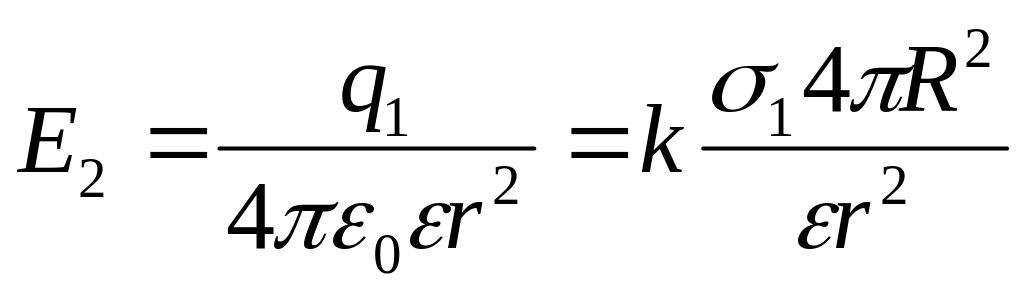 . (3)
. (3)
4. Для
![]() ,
але з внутрішньої сторони другої сфери
,
але з внутрішньої сторони другої сфери
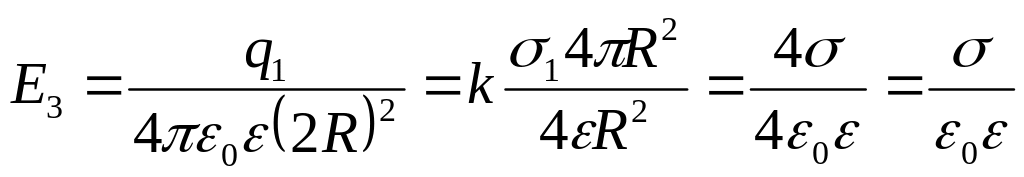 . (4)
. (4)
5. Для , але з зовнішньої сторони другої сфери
 . (5)
. (5)
6
Рис. 2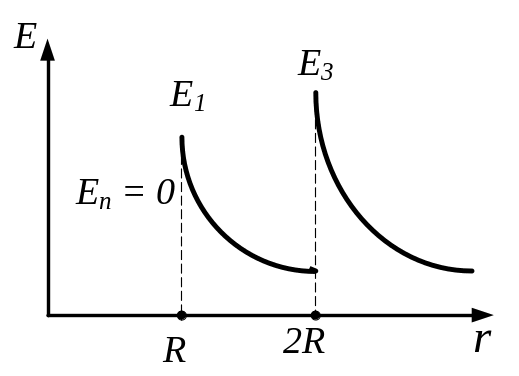
![]()
 .
(6)
.
(6)
Будуємо графік залежності Е(r), використовуючи отримані вирази:
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3

Дано
= 0,1 мкКл/м2
= ?
![]()
![]()
![]()
Розв’язок.
Зробимо малюнок, на якому зображені дві концентричні сфери радіусом R і 2R, по поверхні яких рівномірно розподілені заряди з поверхневою густиною σ1 і σ2, та точка А, в якій визначатимемо напруженість електричного поля.
Вивчаємо розв’язок попередньої задачі і вибираємо формулу (6):

Зробимо підстановку заданих величин у системі СІ:
=
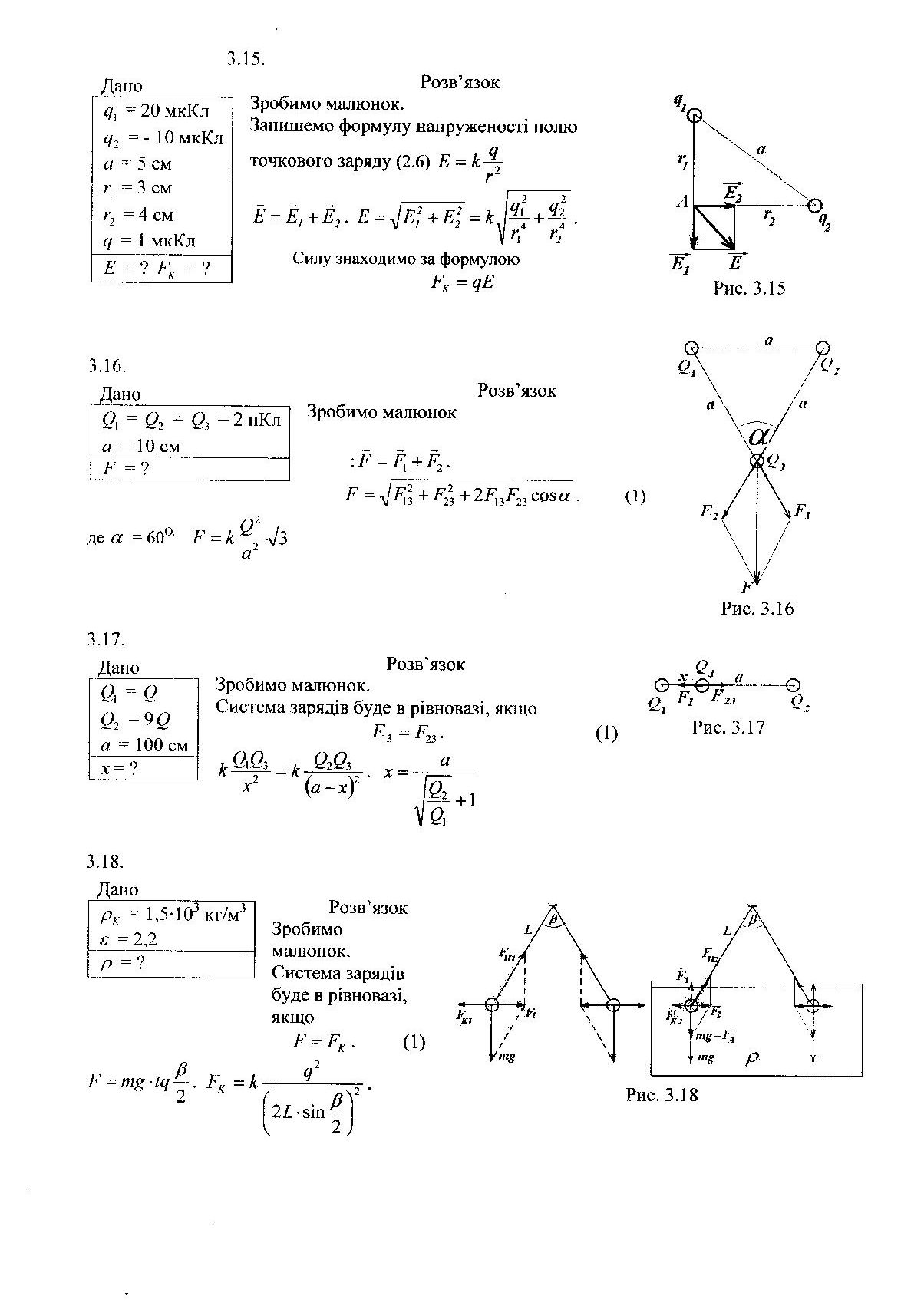
3.55.
Дано
= ?
![]() = 4
= 4
![]() = 10 В
= 10 В
Під час злиття краплин в одну сталими залишаються їхні загальні заряд та об’єм:
![]() (1)
(1)
де
![]() - заряд великої краплі;
- заряд великої краплі;
![]() ,
,
![]() ,
- заряд, ємність і радіус малої краплі;
,
- заряд, ємність і радіус малої краплі;
![]() - радіус великої краплі.
- радіус великої краплі.
Потенціал великої краплі знаходимо за формулою
![]() . (2)
. (2)
Зробимо підстановку заданих величин: =
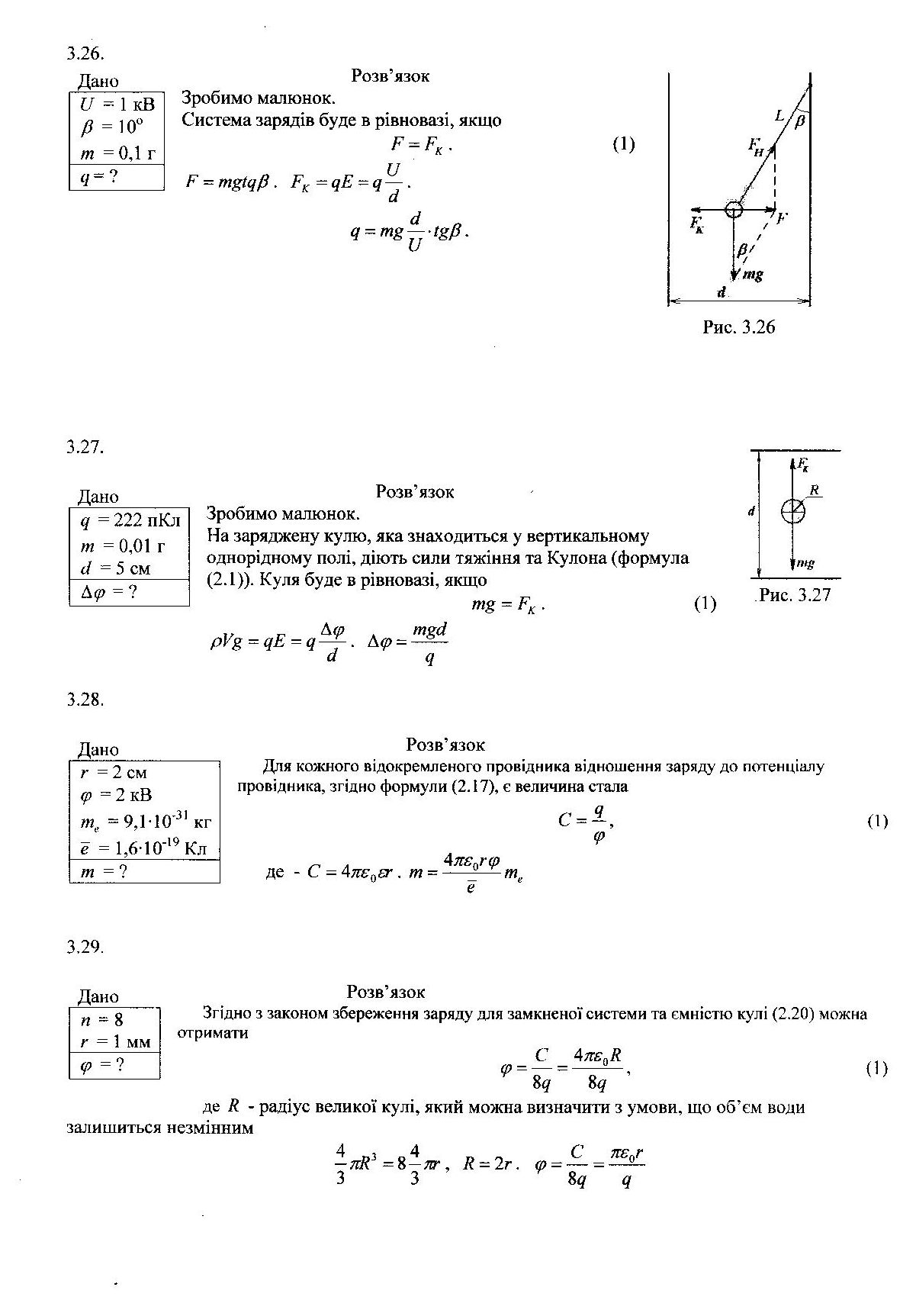
3.56.
Дано
σ1
= 2 мкКл/м2 σ2
= - 0,8 мкКл/м2
= ?
![]() = 0,6 см
= 0,6 см
Електростатичне поле між двома різнойменно зарядженими паралельними нескінченними площинами:
![]() . (1)
. (1)
Для однорідного поля (поля плоского конденсатора) напруженість
![]() ,
(2)
,
(2)
де U — різниця потенціалів між пластинами конденсатора; d — відстань між ними.
З формул (1) і (2) отримаємо:
![]()
Зробимо підстановку заданих величин: =
3.57.

Дано
σ1
= 2σ σ2
= - σ σ
= 20 нКл/м2
![]() = ?,
= ?,
![]() = ?
= ?
Зробимо малюнок:
Електростатичне поле поза двома різнойменно зарядженими паралельними нескінченними площинами дорівнює:
![]() . (1)
. (1)
Зробимо підстановку заданих величин у системі СІ: =
=
3.58.
Дано
= 10 нКл/м2 а
= 10 см
![]() = ?,
= ?,
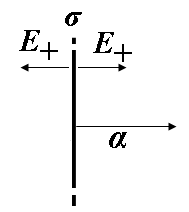
Зробимо малюнок:
Зв’язок між напруженістю та потенціалом поля:
![]() . (1)
. (1)
Звідки різниця потенціалів двох точок поля дорівнює
 , (2)
, (2)
де - відстань від точки поля до площини.
Електростатичне поле рівномірно зарядженої нескінченної площини дорівнює:
![]() . (3)
. (3)
Підставимо (3) у (2) і виконаємо інтегрування
![]()
Зробимо підстановку заданих величин у системі СІ: =
Рис. 1
3.59.
Дано
σ1
= - 2σ
= 50 нКл/м2
= ?
Зробимо малюнок, на якому зображені два коаксіальних нескінченних циліндра радіусом R і 2R, по поверхні яких рівномірно розподілені заряди з поверхневою густиною σ1 і σ2.
Застосуємо теорему Гауса до вектора напруженості електричного поля, тоді її записують так:
1. Для
(1)
2. Для
![]() . (2)
. (2)
3. Для
![]() . (3)
. (3)
4. Для , але з внутрішньої сторони другого циліндра
![]() . (4)
. (4)
5. Для , але з зовнішньої сторони другого циліндра
![]() . (5)
. (5)
6
Рис. 2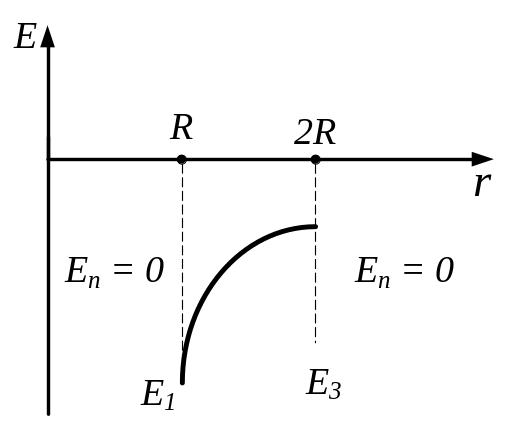
Будуємо графік залежності Е(r) (див. рис. 2), використовуючи отримані вирази (1) - (5).
=
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.60.
Дано
σ1
= σ
= 60 нКл/м2
= ?
Рис. 1
Зробимо малюнок, на якому зображені два коаксіальних нескінченних циліндра радіусом R і 2R, по поверхні яких рівномірно розподілені заряди з поверхневою густиною σ1 і σ2.
Застосуємо теорему Гауса до вектора напруженості електричного поля, тоді для даного випадку її записують так:
1. Для
(1)
2. Для
![]() . (2)
. (2)
3. Для
![]() . (3)
. (3)
4. Для , але з внутрішньої сторони другого циліндра
![]() . (4)
. (4)
5. Для , але з зовнішньої сторони другого циліндра
![]() . (5)
. (5)
4
Рис. 2
![]() .
(6)
.
(6)
Будуємо графік залежності Е(r) (див. рис. 2), використовуючи отримані вирази (1) - (5).
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (6):
=
3.61.
Дано
V = 8 Мм/с
= ?
Електричне поле перемішуючі електричний заряд виконує роботу:
![]() , (1)
, (1)
де
![]() - заряд електрона, який дорівнює ………
- заряд електрона, який дорівнює ………
Ця робота йде на зміну кінетичної енергії цього заряду:
![]() , (2)
, (2)
де
![]() - маса електрона, яка дорівнює ……..
- маса електрона, яка дорівнює ……..
Вважаючи початкову швидкість електрона рівною нулю, порівняємо рівняння (1) та (2) і отримаємо розрахункову формулу:
![]() . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.62.
Дано
= 40 мг q
= 1 нКл V
= 10 см/с q0
= 1,33 нКл
= ?
Будемо вважати, що позитивний точковий заряд q0 створює електричне поле, в якому рухається кулька втрачаючи свою кінетичну енергію, тобто електричне поле, гальмуючі кульку, виконує роботу:
![]() . (1)
. (1)
Різниця потенціалів поля, створеного зарядом кульки, дорівнює
![]() , (2)
, (2)
де
- коефіцієнт пропорційності, який
дорівнює
![]() м/Ф; а
м/Ф; а
![]() .
.
Ця робота йде на зміну кінетичної енергії цього заряду:
![]() , (3)
, (3)
вважаючи кінцеву
швидкість кульки рівною нулю(![]() = 0), порівняємо рівняння (1) та (3) і отримаємо
розрахункову формулу:
= 0), порівняємо рівняння (1) та (3) і отримаємо
розрахункову формулу:
![]() . (4)
. (4)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (4):
=
3.63.
Дано
= 9,1∙10-31
кг q
= 1,6-10-19
Кл V
= 106
м/с
= ?
Будемо вважати,
що один електрон створює електричне
поле, в якому рухається другий з початковою
швидкістю
![]() втрачаючи свою кінетичну енергію, тобто
електричне поле, гальмуючі електрон,
виконує роботу:
втрачаючи свою кінетичну енергію, тобто
електричне поле, гальмуючі електрон,
виконує роботу:
. (1)
Різниця потенціалів поля, створеного зарядом першого електрон, дорівнює
![]() , (2)
, (2)
де - коефіцієнт пропорційності, який дорівнює м/Ф; а .
Ця робота йде на зміну кінетичної енергії електрона:
, (3)
вважаючи кінцеву швидкість електрона рівною нулю( = 0), порівняємо рівняння (1) та (3) і отримаємо розрахункову формулу:
![]() . (4)
. (4)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (4):
=
3.64.
Дано
q1
= 6,66 нКл q2
= 13,33 нКл q
= 1,6-10-19
Кл d
= 40 см D
= 25 см
А = ?
Будемо вважати, що одна кулька створює електричне поле, в якому рухатиметься друга, тоді виконана робота дорівнює:
![]() . (1)
. (1)
Різниця потенціалів поля, створеного зарядом першої кульки, дорівнює
![]() , (2)
, (2)
де - коефіцієнт пропорційності, який дорівнює м/Ф; а .
Тоді робота дорівнює:
![]() , (3)
, (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
А =
3.65.
Дано
q = 20 нКл
d
= 1 см σ
= 10 мкКл/м2
А = ?
![]() = 1 см
= 1 см
З
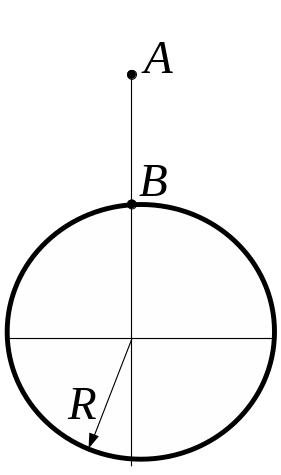
Потенціал у даній точці електричного поля
![]() .
(1)
.
(1)
де
![]() - робота по переміщенню пробного заряду
із нескінченності у дану точку полю;
- робота по переміщенню пробного заряду
із нескінченності у дану точку полю;
![]() - заряд, який переміщають.
- заряд, який переміщають.
З формули (1) робота, яка здійснюється при перенесенні точкового заряду q, дорівнює:
![]() . (2)
. (2)
Потенціал кулі в точці А знаходимо по формулі для точкового заряду:
![]() , (3)
, (3)
де
![]() - заряд кулі,
- заряд кулі,
![]() - відстань від центра кулі, куди ми умовно
поміщаємо її заряд, до т. А.
- відстань від центра кулі, куди ми умовно
поміщаємо її заряд, до т. А.
Тоді робота дорівнює:
![]() . (4)
. (4)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (4):
А =
3.66.
Дано
= 1 г q
= 10 нКл φ1
= 600 В φ2
= 0 V2
= 20 см/с
![]() = ?
= ?
Будемо вважати,
що куля рухається з початковою швидкістю
![]() ,
при цьому збільшує свою кінетичну
енергію, тобто електричне поле виконує
роботу:
,
при цьому збільшує свою кінетичну
енергію, тобто електричне поле виконує
роботу:
, (1)
де
![]() - різниця потенціалів
- різниця потенціалів
Ця робота йде на зміну кінетичної енергії кулі:
![]() , (2)
, (2)
З рівнянь (1) та (2) отримаємо
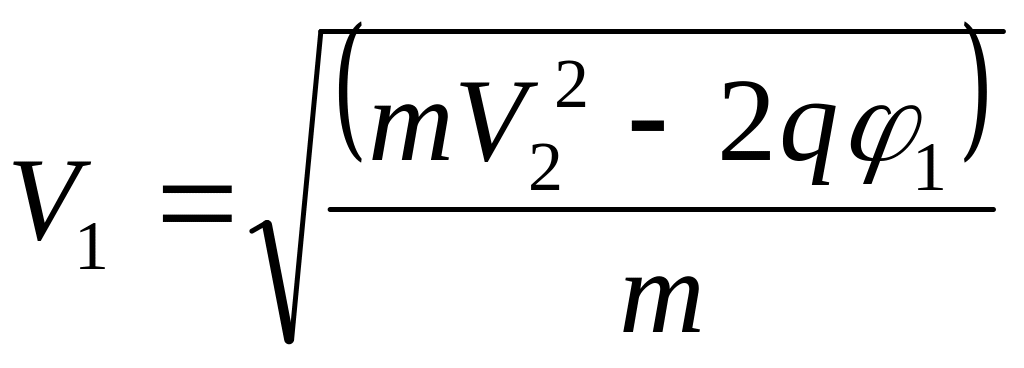 . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.67.
Дано
d1
= 4 см q
= 0,66 нКл
d2
= 2 см А
= 5 10-6
Дж
= ?
Електричне поле виконує роботу проти змінної сили:
![]() , (1)
, (1)
де
![]() - різниця потенціалів двох точок поля,
яку визначаємо за формулою:
- різниця потенціалів двох точок поля,
яку визначаємо за формулою:
, (2)
де напруженість поля, яке створює заряджена нитка в точці простору дорівнює
![]() . (3)
. (3)
Підставимо вираз (3) у формулу (2) і виконавши інтегрування отримаємо
 . (4)
. (4)
Тоді робота дорівнюватиме:
![]() , (5)
, (5)
З рівняння (5) отримаємо формулу для розрахунку лінійної густини заряду на нитці:
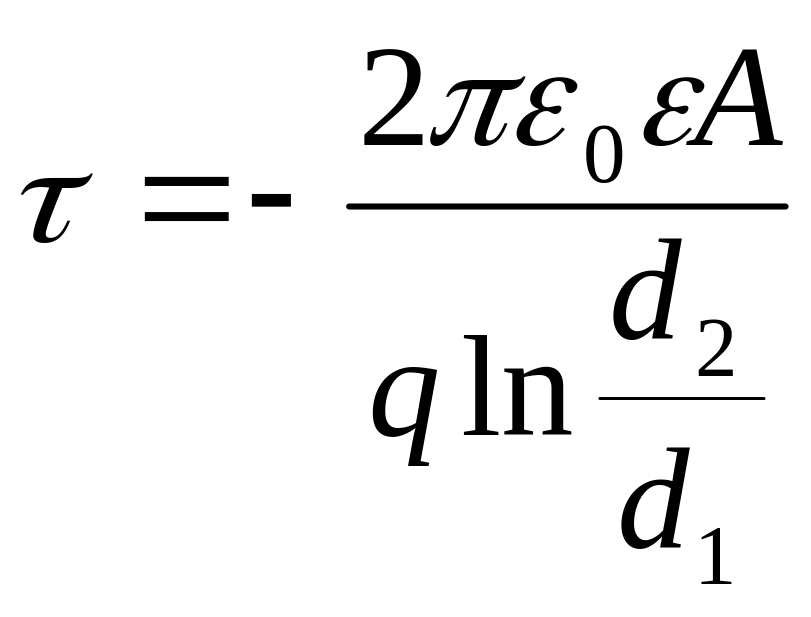 . (6)
. (6)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (6):
=
3.68.
Дано
L1
= 1 см L2
= 4 см q
= 3,2∙10-19
Кл
V1
= 2 105 м/с V2
= 3 106
м/с
= ?
Електричне поле виконує роботу проти змінної сили:
![]() , (1)
, (1)
де - різниця потенціалів двох точок поля, яку визначаємо за формулою:
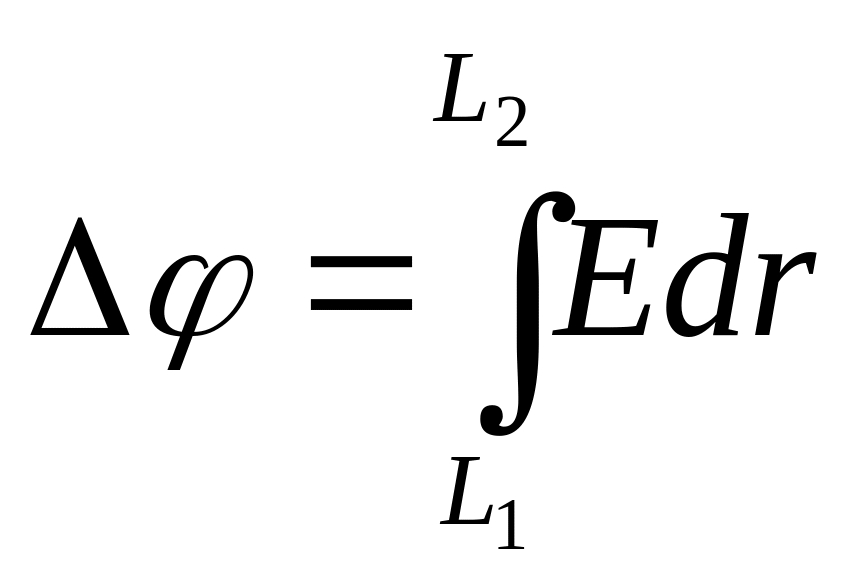 , (2)
, (2)
де напруженість поля, яке створює заряджена нитка в точці простору дорівнює
. (3)
Підставимо вираз (3) у формулу (2) і виконавши інтегрування отримаємо
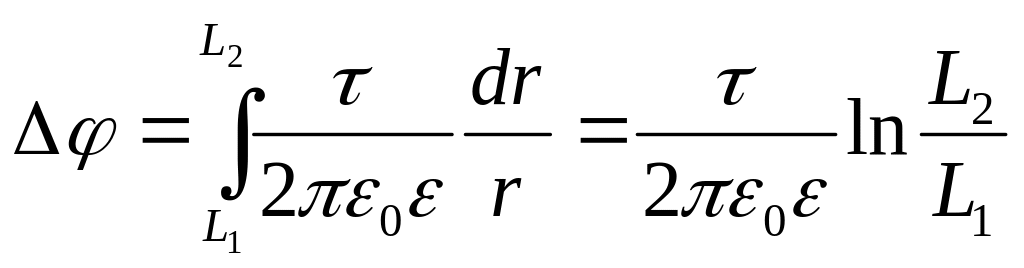 . (4)
. (4)
Тоді робота дорівнюватиме:
![]() , (5)
, (5)
Ця робота йде на зміну кінетичної енергії кулі:
, (6)
де
- маса
![]() -частинки.
-частинки.
З рівнянь (5) та (6) отримаємо
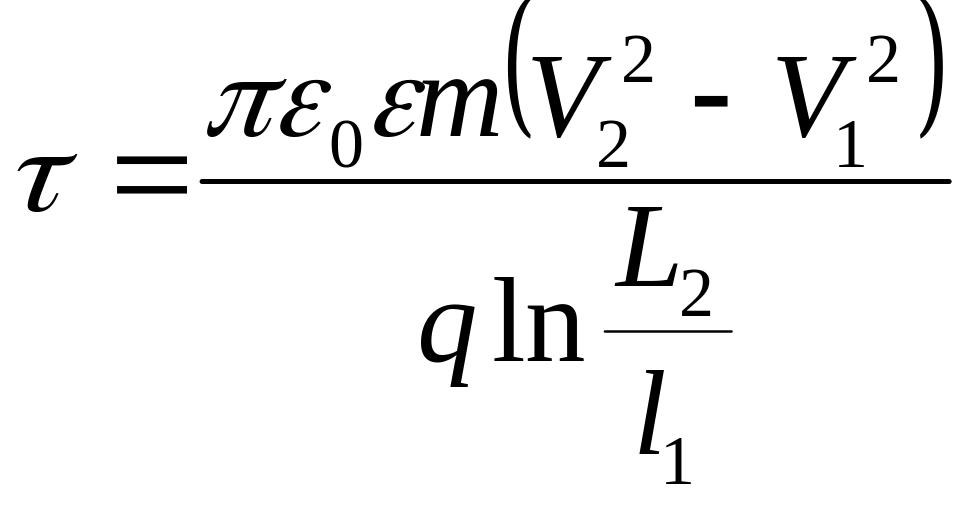 . (7)
. (7)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (7):
=
3.69.
Дано
τ = 0,2 мкКл/м L1
= 1 см L2
= 0,5 см q
= - 1,6∙10-19
Кл
V1
= 0
V2
= ?
Електричне поле виконує роботу проти змінної сили:
, (1)
де - різниця потенціалів двох точок поля, яку визначаємо за формулою:
, (2)
де напруженість поля, яке створює заряджена нитка в точці простору, дорівнює
. (3)
Підставимо вираз (3) у формулу (2) і виконавши інтегрування отримаємо
. (4)
Тоді робота дорівнюватиме:
, (5)
Ця робота йде на зміну кінетичної енергії:
![]() ,
де
- маса електрона. (6)
,
де
- маса електрона. (6)
З рівнянь (5) та (6) отримаємо
![]() . (7)
. (7)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (7):
V2 =
3.70.
Дано
q = 0,66 нКл
d
= 2 см А
= 5 10-6
Дж
= ?
Електричне поле виконує роботу проти змінної сили:
![]() , (1)
, (1)
де - різниця потенціалів двох точок поля, яку визначаємо за формулою:
![]() , (2)
, (2)
де напруженість поля, яке створює заряджена нескінченна площина в точці простору, дорівнює
![]() . (3)
. (3)
Підставимо вираз (3) у формулу (2) і виконавши інтегрування отримаємо
![]() . (4)
. (4)
Тоді робота дорівнюватиме:
![]() , (5)
, (5)
З рівнянь (5) отримаємо
![]() . (6)
. (6)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (6):
=
3.71.
Дано
d = 4 см
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() = ?
= ?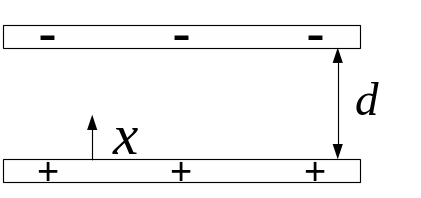
Зробимо малюнок:
Вважаючи поле в конденсаторі однорідним, запишемо шлях, який пройдуть частинки до зустрічі, рухаючись з постійним прискоренням без початкової швидкості:
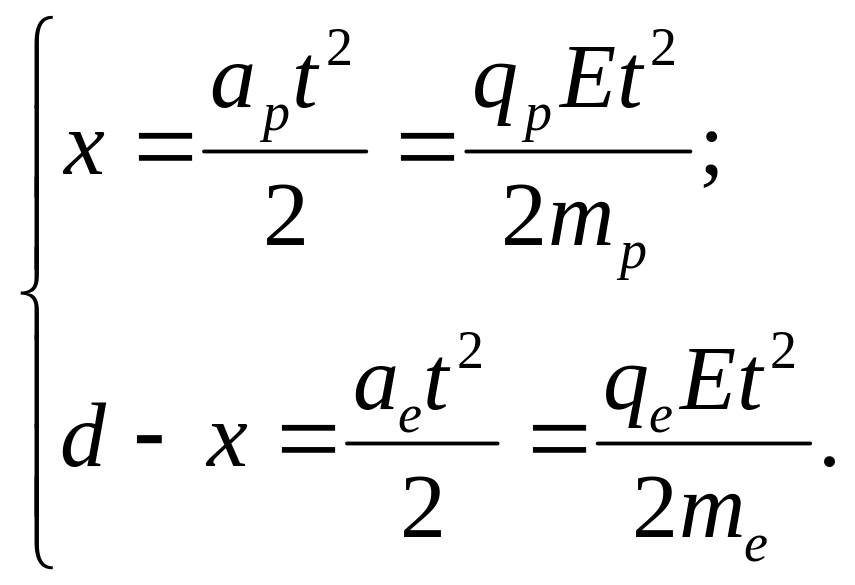 (1)
(1)
З відношення рівнянь цієї системи отримаємо
![]() . (2)
. (2)
Розв’язуємо останнє рівняння відносно :
= (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.72.
Дано
d = 1 см
=
=
= ?
![]() =
=
![]() =
=
Зробимо малюнок:
Вважаючи поле в конденсаторі однорідним, запишемо шлях, який пройдуть частинки до зустрічі, рухаючись з постійним прискоренням без початкової швидкості:
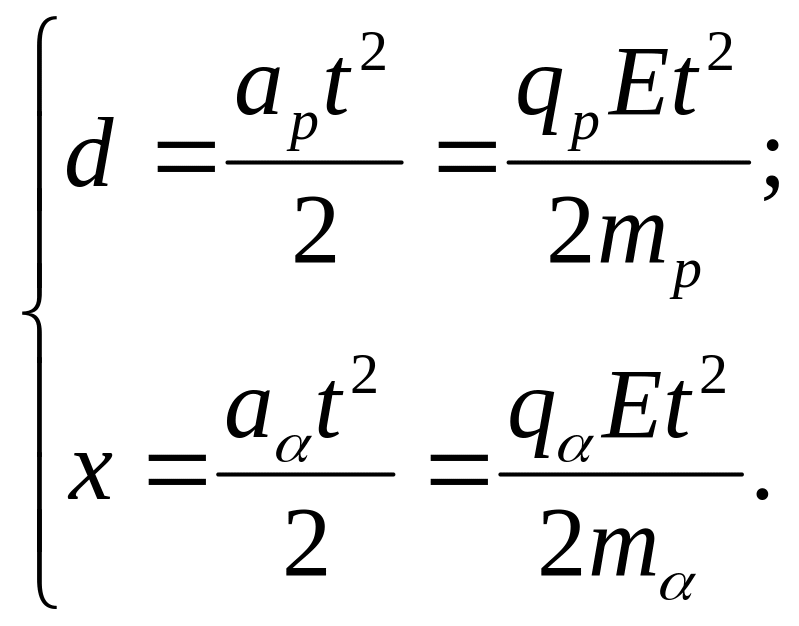 (1)
(1)
З відношення рівнянь цієї системи отримаємо
![]() . (2)
. (2)
Розв’язуємо останнє рівняння відносно :
= (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3
Дано
d = 5,3 мм
=
=
V
= 108 м/с
= ?
= ?
Розв’язок.
Електричне поле виконує роботу по переміщенні електрона:
![]() , (1)
, (1)
Ця робота йде на зміну кінетичної енергії:
![]() ,
де
,
де
![]() - маса електрона, а
= 0 (2)
- маса електрона, а
= 0 (2)
З рівнянь (1) і (2) отримаємо
![]() . (3)
. (3)
Напруженість поля в конденсаторі визначається формулою:
![]() . (4)
. (4)
З (4) визначаємо поверхневу густину заряду на пластинах конденсатора
![]() . (5)
. (5)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вирази (3) і (5):
=
=
3.74.
Дано
d = 2 см U
= 120 В
=
=
h
= 3 мм
= ?
Однорідне електричне поле виконує роботу по переміщенні електрона:
![]() , (1)
, (1)
де напруженість поля в конденсаторі пов’язана з різницею потенціалів на його пластинах рівнянням:
![]() . (2)
. (2)
Ця робота йде на зміну кінетичної енергії:
![]() , (3)
, (3)
де - маса електрона, а = 0.
З рівнянь (1), (2) і (3) отримаємо
![]() . (4)
. (4)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (4):
=
3.75.
Дано
V0
= 9 106
м/с d
= 1 см U
= 100 В
=
=
![]() = 10 нс
= 10 нс
![]() = ?
= ?
![]() = ?
= ?
![]() = ?
= ?
З
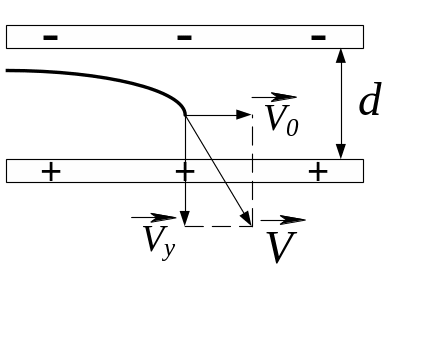
Повне прискорення електрона визначаємо з формули закону Ньютона:
![]() . (1)
. (1)
Вертикальну складову швидкості електрона знаходимо з формули:
![]() . (2)
. (2)
Повна швидкість електрона дорівнює
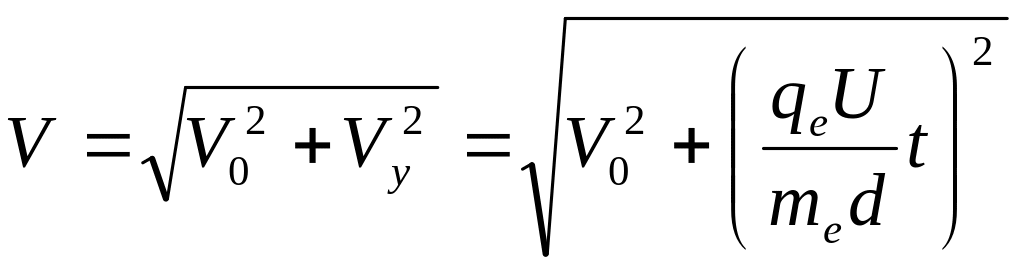 . (3)
. (3)
Тоді тангенціальне прискорення знаходимо за формулою:
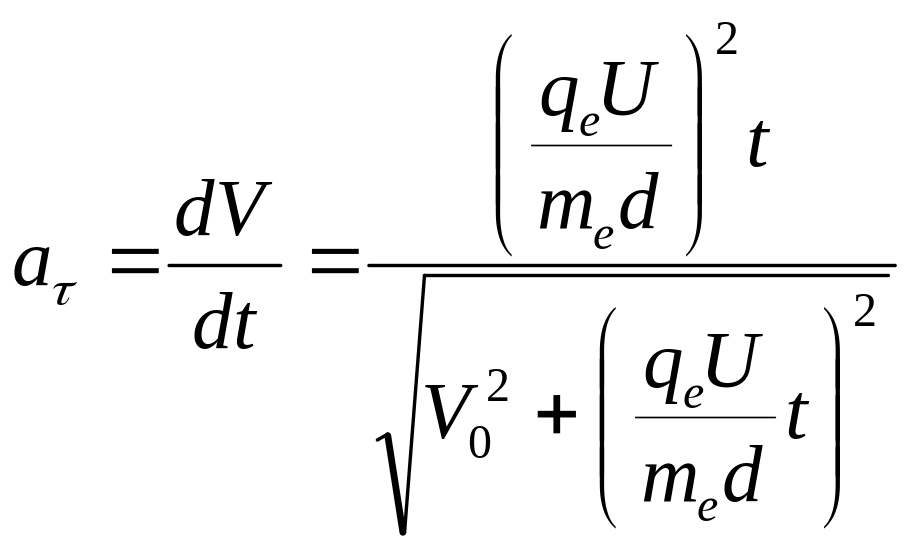 . (4)
. (4)
Тоді нормальне прискорення знаходимо за формулою:
![]() . (5)
. (5)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вирази (1), (4) і (5): =
=
=
3.76.
Дано
V0
= 9 106
м/с Е
= 10 кВ/м
=
=
= ?
![]() = 5 см
= 5 см
З

Вертикальну складову швидкості електрона знаходимо з формули:
![]() . (1)
. (1)
Повна швидкість електрона дорівнює
 . (2)
. (2)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (2):
=
3.77.
Дано
φ = 300 В Q
= 0,2 мкКл
А = ?
З
Рис. 1
Електричне поле виконує роботу по переміщенні заряду:
![]() , (1)
, (1)
Різницю потенціалів поля, яке створюється кулею, визначаємо за формулою:
![]() , (2)
, (2)
де
![]() = 2
,
а
= 2
,
а
![]() = 4
;
= 4
;
![]() - заряд кулі.
- заряд кулі.
Тоді робота дорівнює
![]() . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
А =
3.78.
Дано
р = 100 пКл∙м Е
= 200 кв/м α
= 180°
А = ?
З
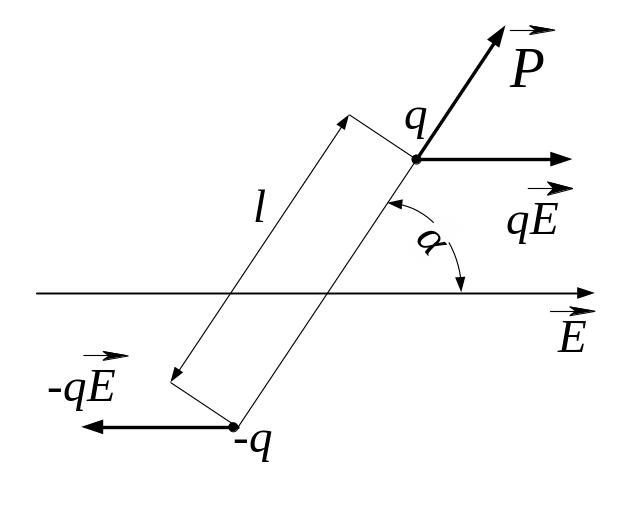
Елементарна робота
![]() під час повороту диполя на кут
під час повороту диполя на кут
![]() виражається формулою
виражається формулою
![]() , (1)
, (1)
де
![]() - механічний момент пари сил Кулона.
- механічний момент пари сил Кулона.
Повна робота при повороті від 0 до кута
![]() . (2)
. (2)
Виконавши інтегрування, отримаємо
![]() . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
А =
3.79.
Дано
m = 200 мкг
Q
= 40 нКл
= 200 В V2
= 10 м/с
= ?
Електричне поле виконує роботу по переміщенню порошини:
![]() , (1)
, (1)
Ця робота йде на зміну кінетичної енергії:
![]() . (2)
. (2)
Початкову швидкість порошини визначаємо з рівнянь (1) і (2):
![]() . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3. 80.
Дано
Q1
= 2 мкКл Q2
= - 2 мкКл
= 10 см Q
= 0,5 мкКл
= ?
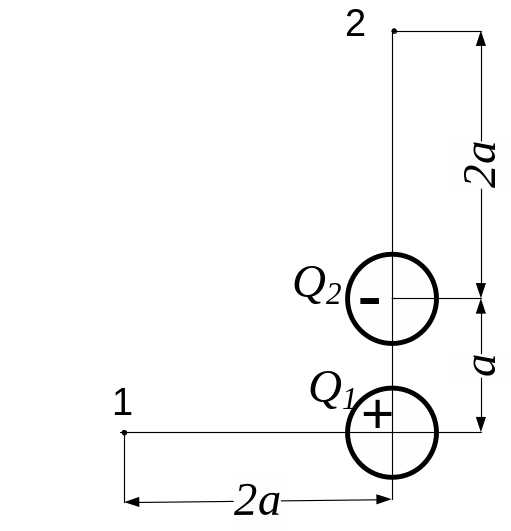
Електричне поле виконує роботу проти змінної сили:
, (1)
де - різниця потенціалів двох точок поля, які визначаємо за формулами:
![]() . (2)
. (2)
Вирази (2) підставляємо в(1)
![]() . (3)
. (3)
Підставимо вираз (3) у формулу (1) і зробимо підстановку заданих величин у системі СІ в отриманий вираз:
=
=
3
Дано
Т = 10 еВ U
= 8 В
=
=
![]() = ?
= ?
Розв’язок.
Електричне поле виконує роботу по переміщенні електрона:
![]() , (1)
, (1)
Ця робота йде на зміну кінетичної енергії:
![]() , (2)
, (2)
де - маса електрона; - заряд електрона.
З рівнянь (1) і (2) отримаємо
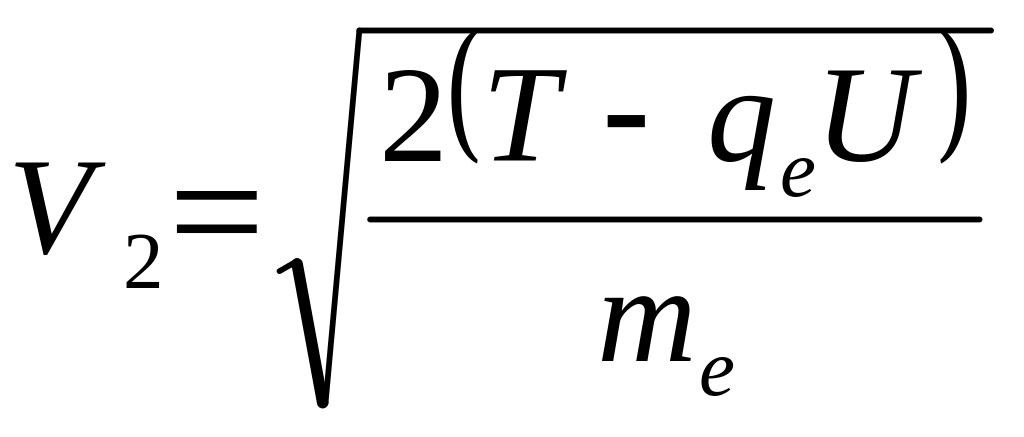 . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.82.
Дано
V = 105 м/с d
= 8 мм U
= 120 В
=
=
= ?,
= ?
Однорідне електричне поле виконує роботу по переміщенні електрона:
![]() . (1)
. (1)
Ця робота йде на зміну кінетичної енергії:
, (2)
де - маса електрона, а = 0.
З рівнянь (1) і (2) отримаємо
. (3)
Напруженість поля в конденсаторі пов’язана з різницею потенціалів на його пластинах рівнянням:
![]() . (4)
. (4)
З теореми Гауса випливає, що напруженість поля між двома різнойменно зарядженими паралельними нескінченними площинами:
![]() . (5)
. (5)
З рівнянь (4) і (5) отримаємо
. (6)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вирази (3) і (6):
=
=
3.83.
Дано
m = 5 нг
= 10
= 1 MB
=
=
![]() = ?,
= ?
= ?,
= ?
Електричне поле виконує роботу по переміщенню порошини:
![]() . (1)
. (1)
Ця робота йде на зміну кінетичної енергії:
![]() . (2)
. (2)
З рівнянь (1) і (2) отримаємо зміну кінетичної енергії порошини:
![]() , (3)
, (3)
а також швидкість V, яку набула порошина
![]() . (4)
. (4)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ в вирази (3) і (4):
=
=
3.84.
Дано
m = 5 нг
= 10 φ1
= 400 В
![]() =
=
![]() =
=
![]() = ?
= ?
З
Рис. 3.84
Електричне поле виконує роботу по гальмуванню протона:
![]() , (1)
, (1)
де різниця потенціалів дорівнює
![]() . (2)
. (2)
Потенціал точки
поля![]() ,
створеного металевою кулею дорівнює
,
створеного металевою кулею дорівнює
![]() , (3)
, (3)
де - заряд кулі, який дорівнює
![]() . (4)
. (4)
Підставляємо вираз (4) у (3)
![]() ,
,
а отримане значення формулу (2):
![]() . (5)
. (5)
Робота, що визначається формулою (1), йде на зменшення кінетичної енергії протона до нуля:
![]() . (6)
. (6)
З рівнянь (1) і (6) отримаємо мінімальну швидкість, яку повинен мати протон, щоб він міг досягти поверхні зарядженої кулі:
![]() . (7)
. (7)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ в вираз (7):
=
3.85.
Дано
Е = 200 В/м V0
= 2 Мм/с
=
=
![]()
![]() = ?,
= ?,
Однорідне електричне поле виконує роботу по гальмуванню електрона:
![]() . (1)
. (1)
Ця робота йде на зміну кінетичної енергії:
![]() , (2)
, (2)
де - маса електрона.
З рівнянь (1) і (2) отримаємо
![]() . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.86.
Дано
φ1
= 100 В V1
= 6 Мм/с
=
=
![]()
![]() = ?,
= ?,
Однорідне електричне поле виконує роботу по гальмуванню електрона:
![]() . (1)
. (1)
Ця робота йде на зміну кінетичної енергії:
![]() , (2)
, (2)
де - маса електрона.
З рівнянь (1) і (2) отримаємо
![]() . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3. 87.
Дано
Q1
= 6 нКл Q2
= 3 нКл Q2
= - 2 мкКл
= ?
![]() = 60 см
= 60 см![]() = 0,5
= 0,5
Будемо вважати, що перший заряд створює електричне поле, в якому рухається другий заряд, тобто електричне поле виконує роботу:
![]() . (1)
. (1)
Різниця потенціалів поля, створеного першим зарядом, дорівнює
![]() , (2)
, (2)
де - коефіцієнт пропорційності, який дорівнює м/Ф; а .
Підставимо вираз (2) у формулу (1) і зробимо підстановку заданих величин у системі СІ в отриманий вираз:
=
=
3.88.
Розв’язок.
Дано
τ = 10 нКл/м Т1
= 200 еВ
=
![]() = ?,
= ?,
Електричне поле виконує роботу по переміщенню електрона:
![]() . (1)
. (1)
Зв’язок між напруженістю та потенціалом поля:
. (2)
Звідки різниця потенціалів двох точок поля дорівнює
![]() . (3)
. (3)
Теорему Гауса можна застосувати і до вектора напруженості електричного поля, тоді ЇЇ для нескінченно довгої зарядженої нитки записують так:
![]() . (4)
. (4)
З виразу (4) отримаємо
![]() . (5)
. (5)
Підставляємо вираз (5) у вираз (3) і інтегрування:
![]() . (6)
. (6)
Ця робота йде на зміну кінетичної енергії:
![]()

З рівнянь (1), (6) і (7) отримаємо
![]() . (8)
. (8)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (8):
=
3.89.
Дано
V0
= 3 Мм/с Е
= 150 В/м
= 0,1 мкс
=
=
= ?,
= ?
Завдяки силі Кулона, яка перпендикулярна до швидкості електрона, він рухатиметься по колу з постійною швидкістю і нормальним прискоренням, яке можна визначити із другого закону Ньютона:
![]() , (1)
, (1)
звідки
![]() . (2)
. (2)
Швидкість знаходимо згідно з формулою:
![]() . (3)
. (3)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вирази (2) і (3):
=
=
3.90.
Дано
U = 90 В
= 1 нКл
= ?,
![]() = 60 см2
= 60 см2
Ємність плоского конденсатора дорівнює
![]() . (1)
. (1)
З визначення ємності маємо
![]() . (2)
. (2)
Завдяки силі Кулона, яка перпендикулярна до швидкості електрона, він рухатиметься по колу з постійною швидкістю і нормальним прискоренням, яке можна визначити із другого закону Ньютона:
, (3)
звідки
. (4)
Для одержання відповіді, прирівняємо праві частини рівнянь (1) і (2), визначимо з цього виразу відстань між пластинами конденсатора і зробимо підстановку заданих величин у системі СІ в отриманий вираз: =
=
3.91.
Дано
S = 0,01 м2 d
= 5 мм U0
= 300 В
U = ?,
Ємність плоского
конденсатора повітряного
![]() і з заповненням ебонітом
і з заповненням ебонітом
![]() дорівнює
дорівнює
![]() . (1)
. (1)
З (1) визначаємо різницю потенціалів, яка при цьому встановиться між пластинами
![]() . (2)
. (2)
Робимо розрахунок: U =
3.92.
Дано
ε = 3,2 r
= 1 см R
= 3,0 см.
С1
= ?,
Ємність конденсатора дорівнює
![]() . (1)
. (1)
Різниця потенціалів двох точок поля дорівнює
. (2)
Модуль напруженості поля, створеного нескінченно довгого прямого рівномірно зарядженого циліндра:
. (3)
Вираз (3) підставляємо в (2) і виконуємо інтегрування:
![]() . (4)
. (4)
З (1) і (4) визначаємо ємність С1 одиниці довжини такого кабелю:
![]() . (5)
. (5)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (5):
С1 =
3.93.
Дано
r
= 10 см R
= 10,5 см ε
=
С1
= ?, R0
= ?
Ємність конденсатора дорівнює
. (1)
Різниця потенціалів двох точок поля дорівнює
. (2)
Модуль напруженості поля, створеного зарядженою сферою:
![]() . (3)
. (3)
Вираз (3) підставляємо в (2) і виконуємо інтегрування:
![]() . (4)
. (4)
З (1) і (4) визначаємо ємність С1:
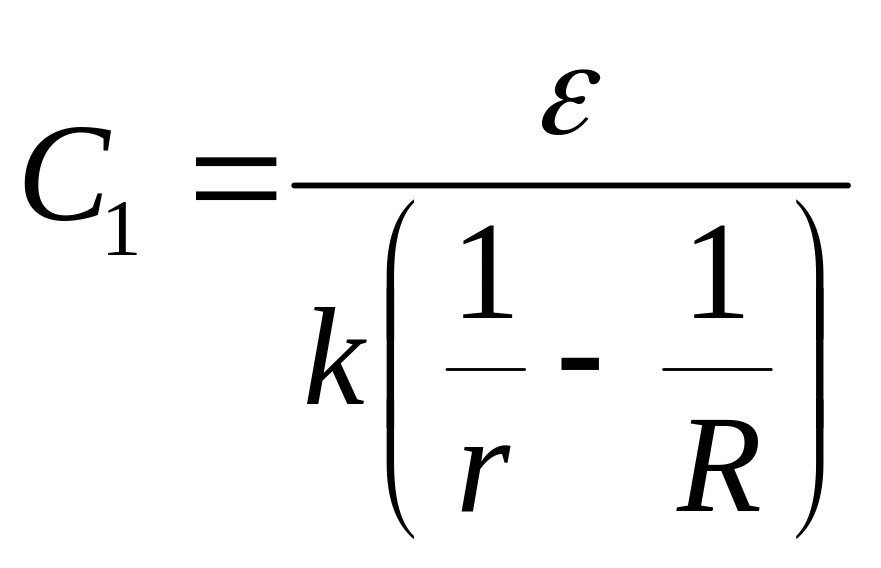 . (5)
. (5)
Куля, занурена в масло, матиме таку ємність
![]() . (6)
. (6)
З виразів (5) і (6) визначаємо радіус кулі
![]() . (7)
. (7)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вирази (5) і (7):
С1 = R0 =
3.94.
Дано
r
= 1 см R
= 4 см ε
= 1 U
= 3 кВ L
= 3 см
Е = ?
Ємність конденсатора дорівнює
![]() . (1)
. (1)
Різниця потенціалів двох точок поля дорівнює
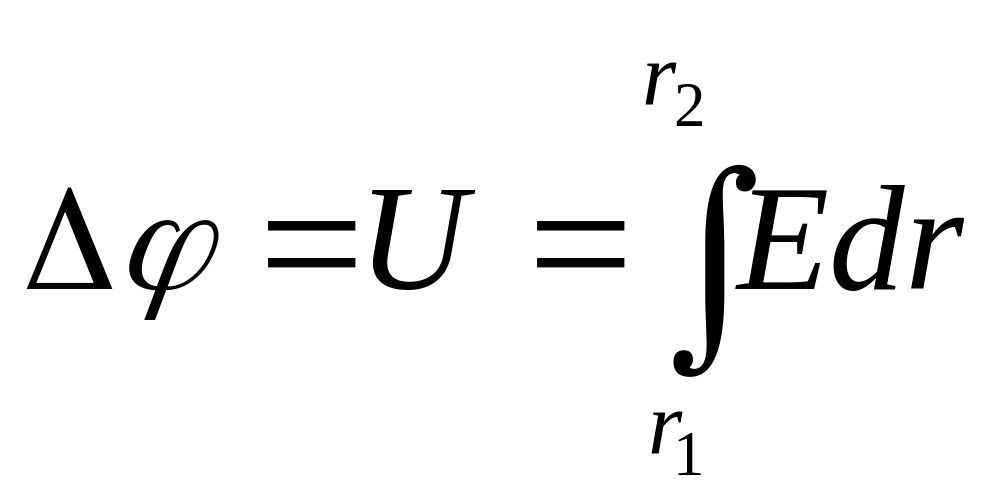 . (2)
. (2)
Модуль напруженості поля, створеного зарядженою сферою:
. (3)
Вираз (3) підставляємо в (2) і виконуємо інтегрування:
![]() . (4)
. (4)
З (1) і (4) визначаємо ємність С:
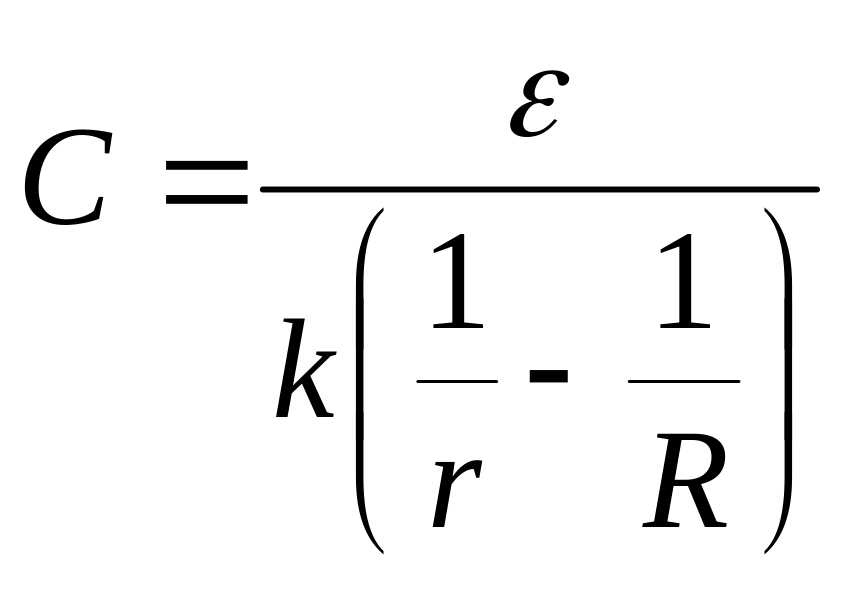 . (5)
. (5)
З формул (1) і (5) визначаємо заряд конденсатора
![]() . (6)
. (6)
Тоді з формул (3) і (5) отримаємо
![]() . (6)
. (6)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (6):
Е =
3.95.
Дано
r
= 1 см R
= 4 см ε
= 1 U
= 3 кВ L1
= 3 см L2
= 2 см
=
=
= ?
Неоднорідне електричне поле виконує роботу по переміщенню електрона:
![]() . (1)
. (1)
Яка піде на зміну кінетичної енергії електрона ( = 0 згідно з умовою задачі):
![]() . (2)
. (2)
Різниця потенціалів двох точок поля дорівнює
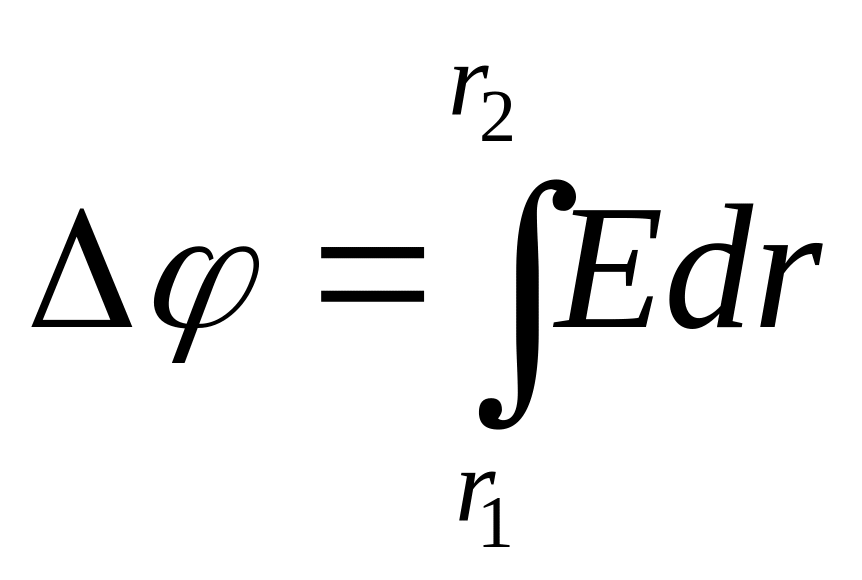 . (3)
. (3)
Модуль напруженості поля, створеного зарядом сфери:
. (4)
Вираз (4) підставляємо в (3) і виконуємо інтегрування:
![]() . (5)
. (5)
Ємність конденсатора дорівнює
. (6)
З (5) і (6) визначаємо ємність конденсатора:
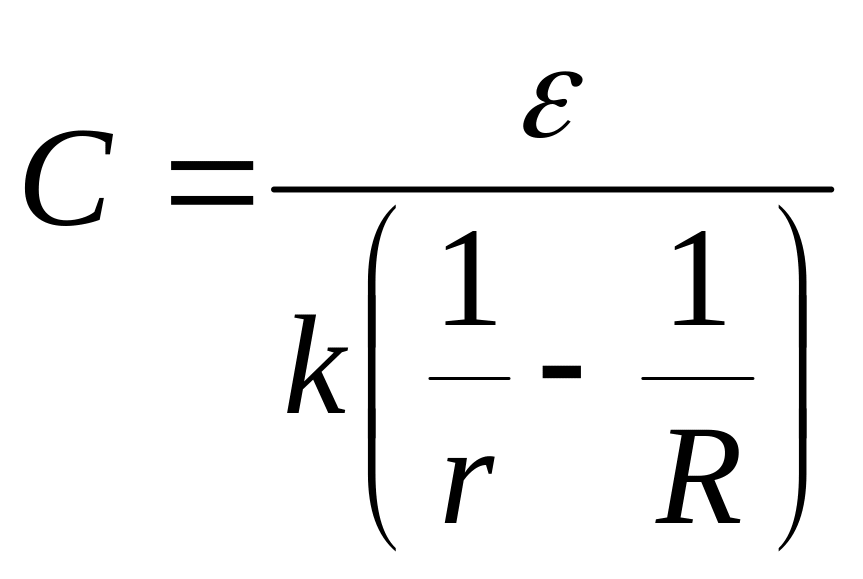 . (7)
. (7)
З формул (6) і (7) визначаємо заряд конденсатора
. (8)
Тоді з формул (5) і (8) визначаємо різницю потенціалів кінцевих точок руху електрона:
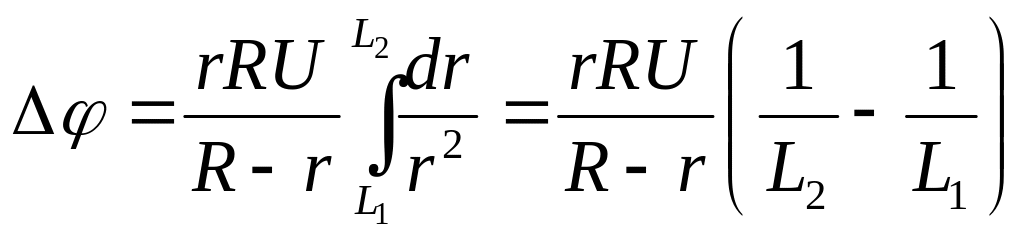 . (9)
. (9)
А з формул (1), (2) і (9) визначаємо швидкість електрона:
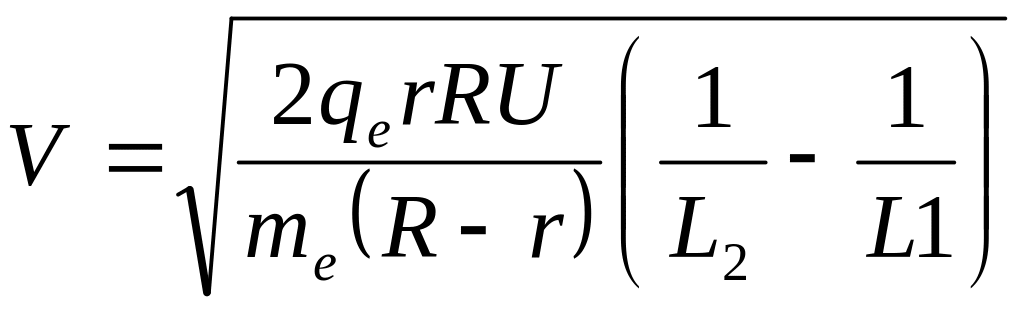 . (10)
. (10)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вираз (10):
=
3.96.
Дано
U = 6 В
C1
= 2 мкФ С2
= 4 мкФ
![]() = ?,
= ?,
![]() = ?
= ?
З

При послідовному з’єднанні конденсаторів заряд на пластинах однаковий, а ємність дорівнює
![]() . (1)
. (1)
Ємність конденсатора дорівнює
. (2)
Тоді заряд на пластинах конденсаторів дорівнює
![]() . (3)
. (3)
З формули (2) визначаємо різницю потенціалу на обкладках другого конденсатора:
![]() . (4)
. (4)
Зробимо підстановку заданих величин у системі СІ в отримані вирази (3) і (4):
=
=
3.97.
Дано
W2
= 10 Дж
![]() = 2 см
= 2 см![]() = 3 см
= 3 см
![]() = ?
= ?
Заряд, який був на першій кулі до її зіткнення з другою кулею дорівнює заряду обох куль після зіткнення:
![]() . (1)
. (1)
Заряд другої кульки визначимо з формули енергії:
![]() . (2)
. (2)
Тобто з (2) маємо
![]() . (3)
. (3)
Враховуючі, що потенціали обох куль після зіткнення будуть однаковими, то знайдемо відношення їхніх енергій:
![]() . (4)
. (4)
З останнього рівняння визначаємо енергію першої кулі після зіткнення:
![]() . (5)
. (5)
Користуючись формулою енергії зарядженої кулі (2) і виразом (5), визначимо заряд першої куль після зіткнення:
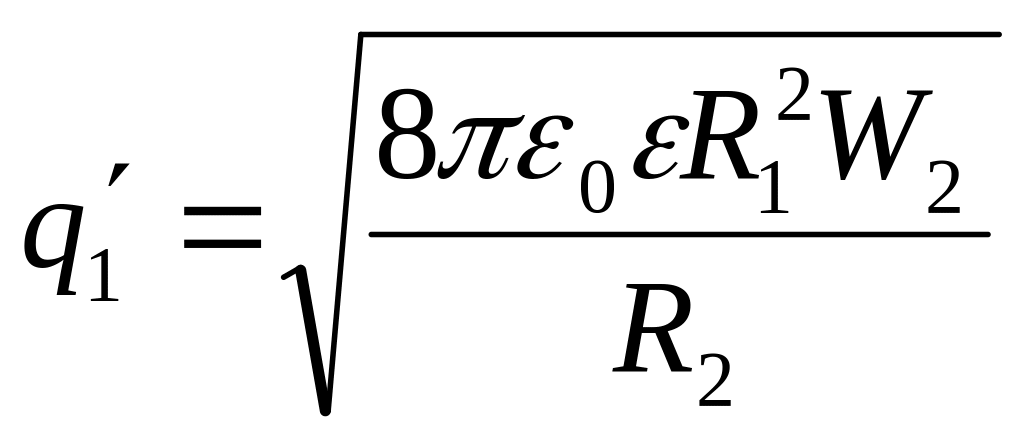 . (6)
. (6)
Для отримання відповіді, зробимо підстановку (3) і(6) у вираз (1) та підставимо задані в задачі величини у системі СІ в отриманий вираз:
=
=
3.98.
Дано
S = 0,01 м2 F
= 30 мН ε
= 6
= ?, Е = ?,
![]() = ?
= ?
Робота при незначному
![]() зміщенні пластин конденсатора дорівнює
зміщенні пластин конденсатора дорівнює
![]() . (1)
. (1)
Звідкіля отримаємо вираз для сили взаємодії пластин конденсатора:
![]() . (2)
. (2)
З (2) можна визначити заряд, що знаходяться на пластинах:
![]() . (3)
. (3)
Напруженість Е поля між пластинами визначаємо за формулою, користуючись виразом (3):
![]() . (4)
. (4)
Об'ємну густину енергії всередині конденсатора визначаємо за відомою формулою, та користуючись виразом (3):
![]() . (5)
. (5)
Для отримання відповіді, зробимо підстановку заданих величин у системі СІ у вирази (3), (4) і (5): = Е = =
3.99. Між пластинами плоского конденсатора вкладена тонка слюдяна пластинка. Який тиск р діє на цю пластинку при напруженості електричного поля Е = 1 МВ/м?
3.99.
Дано
Е =
1 МВ/м
![]() = ?
= ?![]()
Зробимо малюнок, на якому зображена тонка слюдяна пластинка, яка розміщена між пластинами зарядженого плоского конденсатора. Вважаємо, що пластини нескінченно великі і одна з них створює електричне поле напруженістю
![]() , (1)
, (1)
де
- поверхнева густина заряду на пластині;
= 8,85∙10-12
Ф/м – електрична стала;
![]() - діелектрична проникність речовини (
= 1 для вакууму).
- діелектрична проникність речовини (
= 1 для вакууму).
Друга пластина знаходиться в цьому полі і на неї діє сила
![]() . (2)
. (2)
Як відомо, тиск, створений силою, дорівнює:
![]() . (3)
. (3)
В вираз (3) підставляємо силу з виразу (2) і отримаємо розрахункову формулу:
= (4)
Зробимо підстановку заданих величин у системі СІ у вираз (4):
=
3.100. Площа пластин плоского повітряного конденсатора S = 0,01 м2, відстань між ними d =5 мм. Яка різниця потенціалів була прикладена до пластин конденсатора, якщо відомо, що при розряді конденсатора виділилося = 4,19 мДж теплоти?
3.100.
Дано
S = 0,01 м2 d
=5 мм
= 4,19 мДж
= ?
Вважаємо, що в тепло перетворюється вся енергія зарядженого конденсатора, тобто
![]() , (1)
, (1)
де ємність плоского конденсатора дорівнює
![]() , (2)
, (2)
= 8,85∙10-12 Ф/м – електрична стала; - діелектрична проникність речовини ( = 1 для вакууму).
З виразів (1) і (2) отримаємо розрахункову формулу:
= (3)
Зробимо підстановку заданих величин у системі СІ у вираз (3):
=
3.101.
Площа пластин
плоского повітряного конденсатора S
= 0,01 м2,
відстань між ними
![]() = 2 см. До пластин конденсатора прикладена
різниця потенціалів
= 3 кВ. Яка буде напруженість поля
конденсатора, якщо, не відключаючи його
від джерела напруги, розсунути пластини
до відстані
= 2 см. До пластин конденсатора прикладена
різниця потенціалів
= 3 кВ. Яка буде напруженість поля
конденсатора, якщо, не відключаючи його
від джерела напруги, розсунути пластини
до відстані
![]() = 5 см? Знайти енергію конденсатора після
розсунення пластин.
= 5 см? Знайти енергію конденсатора після
розсунення пластин.
3.101.
Дано
S = 0,01 м2 d1
=2 см
= 5 см
![]() =
=
![]() = 3 кВ
= 3 кВ
![]() = ?
= ?
![]() = ?
= ?
Якщо конденсатор не відключаючи від джерела напруги то можна стверджувати, що
![]() , (1)
, (1)
Електрична енергія відокремленого зарядженого провідника дорівнює
![]() . (2)
. (2)
Для плоского конденсатора
![]() , (3)
, (3)
де
![]() — об'єм,
обмежений пластинами конденсатора.
— об'єм,
обмежений пластинами конденсатора.
Тоді після розсунення пластин конденсатора будемо мати
![]() , (3)
, (3)
= 8,85∙10-12 Ф/м – електрична стала; - діелектрична проникність речовини ( = 1 для вакууму).
Зробимо підстановку заданих величин у системі СІ у вирази (1) і (3) та отримаємо відповіді:
= =
3.102. Розв'язати попередню задачу при умові, що спочатку конденсатор відключається від джерела напруги, а потім розсовуються пластини конденсатора.
3.102.
Дано
S = 0,01 м2 d1
=2 см
= 3 кВ
= 5 см
= ?
= ?
![]()
Якщо конденсатор відключити від джерела напруги то можна стверджувати, що
![]() . (1)
. (1)
Ємність плоского конденсатора дорівнює
![]() , (2)
, (2)
де = 8,85∙10-12 Ф/м – електрична стала; - діелектрична проникність речовини ( = 1 для вакууму).
Підставляємо ємності конденсаторів з виразу (2) у формулу (1) і отримаємо
![]() . (3)
. (3)
Електрична енергія відокремленого зарядженого провідника дорівнює
. (4)
Для плоского конденсатора
, (5)
де — об'єм, обмежений пластинами конденсатора.
Тоді після розсунення пластин конденсатора будемо мати
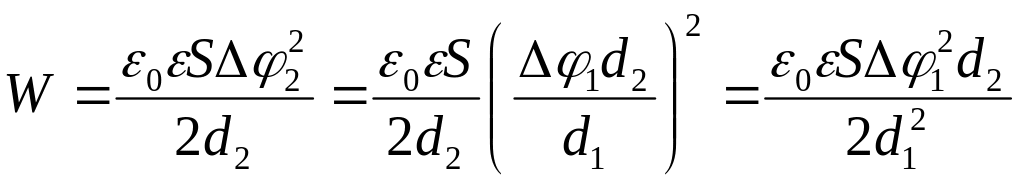 , (6)
, (6)
= 8,85∙10-12 Ф/м – електрична стала; - діелектрична проникність речовини ( = 1 для вакууму).
Зробимо підстановку заданих в умові величин у системі СІ у вирази (3) і (6) та отримаємо відповіді:
= =
3.103.
Плоский
конденсатор заповнений діелектриком
і на його пластини подана деяка різниця
потенціалів. Його енергія при цьому
складає
![]() = 20 мкДж. Після того, як конденсатор
відключили від джерела живлення,
діелектрик вийняли з конденсатора.
Робота, яку треба було здійснити, щоб
вийняти діелектрик склала
= 70 мкДж. Знайти діелектричну проникність
ε діелектрика.
= 20 мкДж. Після того, як конденсатор
відключили від джерела живлення,
діелектрик вийняли з конденсатора.
Робота, яку треба було здійснити, щоб
вийняти діелектрик склала
= 70 мкДж. Знайти діелектричну проникність
ε діелектрика.
3.103.
Дано
= 20 мкДж
= 70 мкДж
= ?
Робота, яку треба здійснити, щоб вийняти діелектрик з конденсатора, дорівнює зміні його енергії:
![]() . (1)
. (1)
Ємність плоского конденсатора дорівнює
![]() , (2)
, (2)
де = 8,85∙10-12 Ф/м – електрична стала; - діелектрична проникність речовини ( = 1 для вакууму).
Для плоского конденсатора енергія електричного поля дорівнює
![]() . (3)
. (3)
Тоді для двох конденсаторів, з урахуванням виразу (2), будемо мати
![]() , (4)
, (4)
де - діелектрична проникність речовини ( = 1 для вакууму).
Підставляємо енергію з виразів (4) у формулу (1) і отримаємо:
![]() . (5)
. (5)
Звідки можна получити вираз для розрахунку діелектричної проникності ε діелектрика:
= (6)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (6) та отримаємо відповідь:
=
3.104. Простір між пластинами плоского конденсатора заповнений діелектриком, діелектрична сприйнятливість якого χ = 0,08. Відстань між пластинами = 5 мм. На пластини конденсатора подана різниця потенціалів = 4 кВ. Знайти поверхневу густина зв'язаних зарядів на діелектрику.
3.104.
Дано
χ = 0,08
= 5 мм
= 4 кВ
![]() = ?
= ?
Д
Рис. 3.104
![]() . (1)
. (1)
Позначимо через
![]() ,
,
![]() - поверхневу густину заряду на пластинах
конденсатора в відсутності діелектрика,
в присутності діелектрика;
- поверхневу густину заряду на пластинах
конденсатора в відсутності діелектрика,
в присутності діелектрика;
![]() - поверхневу густину зв’язаних
(поляризованих) зарядів.
- поверхневу густину зв’язаних
(поляризованих) зарядів.
Спільна дія зарядів густиною і така, якби на межі провідник – діелектрик існує заряд, розподілений з густиною
![]() . (2)
. (2)
Таким чином,
![]() - поверхнева густина «ефективних»
зарядів, які визначають сумарне,
результуюче поле в діелектрику.
- поверхнева густина «ефективних»
зарядів, які визначають сумарне,
результуюче поле в діелектрику.
Як відомо, поверхнева густина заряду пов’язана з відповідними полями такими співвідношеннями:
поле в відсутності діелектрика
![]() ; (3)
; (3)
результуюче поле в діелектрику
![]() . (4)
. (4)
З виразів (2) та (4) отримуємо
![]() . (5)
. (5)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (5) та отримаємо відповідь:
=
3.105. Простір між пластинами плоского конденсатора заповнений склом. Площа пластин конденсатора S = 0,01 м2. Пластини конденсатора притягуються одна до одної з силою F = 4,9 мН. Знайти поверхневу густина зв'язаних зарядів на склі.
Рис. 3.105
3.105.
Дано
= 6 S
= 0,01 м2 F
= 4,9 мН
= ?
Сила притягання пластин плоского конденсатора: а) конденсатор від’єднали від джерела струму; б) приєднаний до джерела струму;
а)
![]() . (1)
. (1)
б)
![]() . (2)
. (2)
Вважаємо, що маємо справу з першим випадком, тобто конденсатор від’єднали від джерела струму. Тоді маємо
![]() . (3)
. (3)
Позначимо через , - поверхневу густину заряду на пластинах конденсатора в відсутності діелектрика, в присутності діелектрика; - поверхневу густину зв’язаних (поляризованих) зарядів.
Спільна дія зарядів густиною і така, якби на межі провідник – діелектрик існує заряд, розподілений з густиною
. (4)
Таким чином, - поверхнева густина «ефективних» зарядів, які визначають сумарне, результуюче поле в діелектрику.
Як відомо, поверхнева густина заряду пов’язана з відповідними полями такими співвідношеннями:
поле в відсутності діелектрика
![]() ; (5)
; (5)
результуюче поле в діелектрику
![]() . (6)
. (6)
З виразів (4) та (6) отримуємо
![]() . (7)
. (7)
Підставляємо в вираз (7) значення напруженості поля з (6) та густини заряду з виразу (3) і отримаємо вираз для розрахунку відповіді:
![]() . (7)
. (7)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (7) та отримаємо відповідь:
=
3.106.
До батареї
з е.р.с у
![]() = 300 В включені два плоских конденсатори
ємностями С1
= 2 пФ і С2
= 3 пФ. Визначити заряд Q
і напругу U
на конденсаторах при їх послідовному
з'єднанні.
= 300 В включені два плоских конденсатори
ємностями С1
= 2 пФ і С2
= 3 пФ. Визначити заряд Q
і напругу U
на конденсаторах при їх послідовному
з'єднанні.
3.106.
Дано
= 300 В С1
= 2 пФ С2
= 3 пФ
Q = ? U1
= ? U2
= ?
Рис. 3.106
При паралельному з'єднанні конденсаторів ємність батареї дорівнює
![]() , (1)
, (1)
при послідовному з'єднанні
![]() . (2)
. (2)
Тобто електрична ємність заданої батареї конденсаторів визначається за формулою:
![]() . (3)
. (3)
Для кожного відокремленого провідника відношення заряду до потенціалу провідника є величина стала
![]() , (4)
, (4)
де — електрична ємність батареї конденсаторів.
Напругу U на конденсаторах визначаємо за формулами:
![]() (5)
(5)
Зробимо підстановку заданих в умові величин у системі СІ у вирази (4) і (5) та отримаємо відповіді:
Q = U1 = U2 =
3.107. До батареї з е.р.с у = 300 В включені два плоских конденсатори ємностями С1 = 2 пФ і С2 = 3 пф. Визначити заряд Q і напругу U на конденсаторах при їх паралельному з'єднанні.
3.107.
Дано
= 300 В С1
= 2 пФ С2
= 3 пФ
Q1
= ? U = ? Q2
= ?
Рис. 3.107
При паралельному з'єднанні конденсаторів ємність батареї дорівнює
, (1)
при послідовному з'єднанні
. (2)
Тобто електрична ємність заданої батареї конденсаторів визначається за формулою:
![]() . (3)
. (3)
Загальний заряд на батареї конденсаторів можна знайти за формулою
![]() , (4)
, (4)
де — електрична ємність батареї конденсаторів.
Заряд на конденсаторах визначаємо за формулами, а перевірку можна виконати за формулою (4):
![]() (5)
(5)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (5) та отримаємо відповіді:
Q1 = Q2 = U = = 300 В
3.108. Конденсатор ємністю С1 = 600 пФ зарядили до різниці потенціалів U1 = 1,5 кВ і відключили від джерела напруги, Потім до нього паралельно приєднали незаряджений конденсатор ємністю С2 = 400 пФ. Визначити енергію, витрачену на утворення іскри, що проскочила при з'єднанні конденсаторів.
3.108.
Дано
U1
= 1,5 кВ С1
= 600 пФ С2
= 400 пФ
Рис. 3.108
![]() = ?
= ?
При паралельному з'єднанні конденсаторів ємність батареї дорівнює
, (1)
при послідовному з'єднанні
. (2)
Тобто електрична ємність заданої батареї конденсаторів визначається за формулою:
. (3)
Загальний заряд на батареї конденсаторів дорівнюватиме заряду на першому конденсаторі
![]() . (4)
. (4)
Визначаємо енергію, витрачену на утворення іскри, що проскочила при з'єднанні конденсаторів з закону збереження енергії:
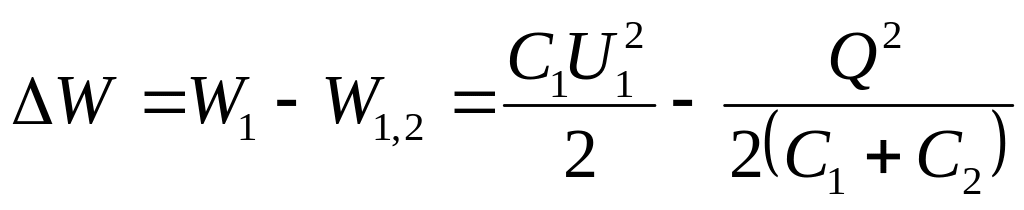 , (5)
, (5)
де
![]() - енергія електричного поля в першому
конденсаторі і в паралельному з’єднанні
конденсаторів.
- енергія електричного поля в першому
конденсаторі і в паралельному з’єднанні
конденсаторів.
Підставляємо заряд з виразу (4) у формулу (5) і отримаємо вираз для розрахунку відповіді:
= (6)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (6) та отримаємо відповідь:
=
3.109. Конденсатори ємністю С1 = 5 мкФ і С2 = 10 мкФ заряджені до напруги U1 = 60 В и U2 = 100 В, відповідно. Визначити напругу на обкладках конденсаторів після їхнього з'єднання обкладками, що мають однойменні заряди.
3.109.
Дано
U1
= 60 В U2
= 100 В С1
= 5 мкФ С2
= 10 мкФ
= ?
Рис. 3.109
Згідно закону збереження кількості заряду можна стверджувати, що заряд на батареї конденсаторів дорівнює сумі зарядів на кожному з них
![]() . (1)
. (1)
Визначити напругу на обкладках конденсаторів після їхнього з'єднання обкладками, що мають однойменні заряди, можна за формулою
![]() . (2)
. (2)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (2) та отримаємо відповідь:
=
3.110. Конденсатор ємністю С1 = 10 мкФ заряджений до напруги U = 10 В. Визначити заряд на обкладках цього конденсатора після того, як паралельно йому був підключений інший, незаряджений, конденсатор ємністю С2 = 20 мкФ.
3.110.
Дано
U1
= 10 В U2
= 0 С1
= 10 мкФ С2
= 20 мкФ
Рис. 3.110
![]() = ?
= ?
Згідно закону збереження кількості заряду можна стверджувати, що заряд на першому конденсаторі дорівнюватиме сумі зарядів на кожному з них після з’єднання
![]() . (1)
. (1)
Визначити напругу на обкладках конденсаторів після їхнього з'єднання обкладками, що мають однойменні заряди, можна за формулою
![]() . (2)
. (2)
Тоді заряд на першому конденсаторі після з’єднання його з другим дорівнюватиме
![]() . (3)
. (3)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (3) та отримаємо відповідь:
=
3.111. Конденсатори ємностями С1 = 2 мкФ, С2 = 5 мкФ і С3 = 10 мкФ з'єднані послідовно і знаходяться під напругою U = 850 В. Визначити напругу і заряд на першому з конденсаторів.
3.111.
Дано
U
= 850 В С1
= 2 мкФ С2
= 5 мкФ С3
= 10 мкФ
= ?
Рис. 3.111
![]() = ?
= ?
При послідовному з’єднанні конденсаторів заряд на кожному з них буде однаковий
![]() , (1)
, (1)
де при послідовному з'єднанні загальна ємність дорівнює
![]() . (2)
. (2)
Підставляємо загальну ємність з виразу (2) у формулу (1) і отримаємо заряд на першому конденсаторі:
![]() . (3)
. (3)
Напруга на першому конденсаторі визначаємо за формулою:
![]() . (4)
. (4)
Заряд з виразу (3) підставляємо у формулу (4) і отримаємо вираз для розрахунку напруги:
= (5)
Зробимо підстановку заданих в умові величин у системі СІ у вирази (3) та (5) і отримаємо відповідь:
= =
3.112. Два конденсатори ємностями С1 = 2 мкФ і С2 = 5 мкФ заряджені до напруги U1 = 100 В та U2 = 150 В, відповідно. Визначити напругу на обкладках конденсаторів після їхнього з'єднання обкладками, що мають різнойменні заряди.
3.112.
Дано
U1
= 100 В U2
= 150 В С1
= 2 мкФ С2
= 5 мкФ
= ?
Рис. 3.112
Після з'єднання конденсаторів обкладками, що мають різнойменні заряди, частина зарядів нейтралізується і на батареї залишиться заряд:
![]() . (1)
. (1)
Тоді напруга на обкладках конденсаторів після їхнього з'єднання обкладками, що мають різнойменні заряди, дорівнюватиме
![]() . (2)
. (2)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (2) та отримаємо відповідь:
=
3.113. Два однакових плоских повітряних конденсатори ємністю 100 пФ кожний з'єднані в батарею послідовно. Визначити, на скільки зміниться ємність цієї батареї, якщо простір між пластинами одного з конденсаторів заповнити парафіном.
3.113.
Дано
С1
= С2
= 100 пФ
= 2
![]() = ?
= ?
Зміну електричної ємності батареї, якщо простір між пластинами одного з конденсаторів, наприклад, другого, заповнити парафіном визначаємо за формулою:
![]() , (1)
, (1)
де
![]() ,
,
![]() - ємності батарей конденсаторів до і
після заповнення парафіном простору
між пластинами другого конденсатора.
- ємності батарей конденсаторів до і
після заповнення парафіном простору
між пластинами другого конденсатора.
При послідовному з'єднанні загальна ємність дорівнює
![]() . (2)
. (2)
Запишемо вирази ємностей отриманих батарей конденсаторів:
![]() (3)
(3)
Підставляємо загальні ємності з виразу (3) у формулу (1) і отримаємо вираз для розрахунку зміни ємності цієї батареї:
= . (4)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (4) і отримаємо відповідь:
=
3.114. Два конденсатори ємностями С1 = 5 мкФ і С2 = 8 мкФ з'єднані послідовно і приєднані до батареї з е.р.с. у = 80 В. Визначити заряд та різницю потенціалів на першому з конденсаторів.
3.114.
Дано
= 80 В С1
= 5 мкФ С2
= 8 мкФ
= ?
= ?
Рис. 3.114
При послідовному з’єднанні конденсаторів заряд на кожному з них буде однаковий
![]() , (1)
, (1)
де при послідовному з'єднанні загальна ємність дорівнює
. (2)
Підставляємо загальну ємність з виразу (2) у формулу (1) і отримаємо заряд на першому конденсаторі:
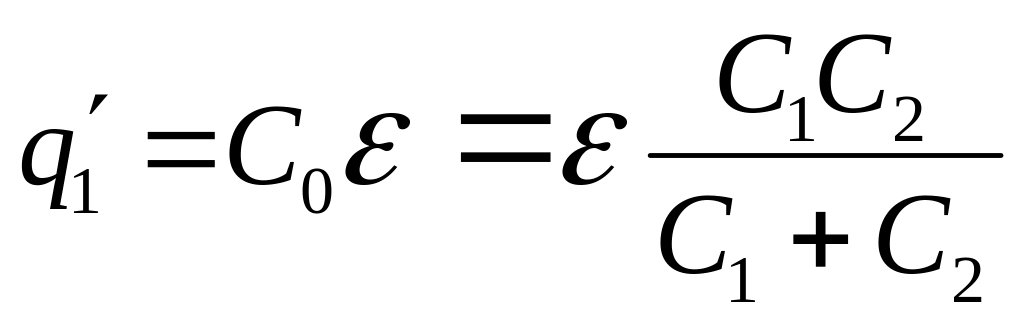 . (3)
. (3)
Напруга на першому конденсаторі визначаємо за формулою:
. (4)
Заряд з виразу (3) підставляємо у формулу (4) і отримаємо вираз для розрахунку напруги:
= (5)
Зробимо підстановку заданих в умові величин у системі СІ у вирази (3) та (5) і отримаємо відповідь:
= =
3.115. Плоский конденсатор складається з двох круглих пластин радіусом R = 10 см кожна. Відстань між пластинами = 2 мм. Конденсатор приєднаний до джерела напруги = 80 В. Визначити заряд Q та напруженість Е поля всередині конденсатора, коли він заповнений склом.
3.115.
Дано
R
= 10 см
= 80 В
= 2 мм
= 6
Q = ? Е
= ?
Ємність плоского конденсатора:
![]() (1)
(1)
де
=
![]() — площа кожної пластини;
- відстань між пластинами.
— площа кожної пластини;
- відстань між пластинами.
Для кожного відокремленого провідника відношення заряду до потенціалу провідника є величина стала
![]() , (2)
, (2)
де — електрична ємність провідника.
З формул (2) та (1) отримуємо заряд конденсатора
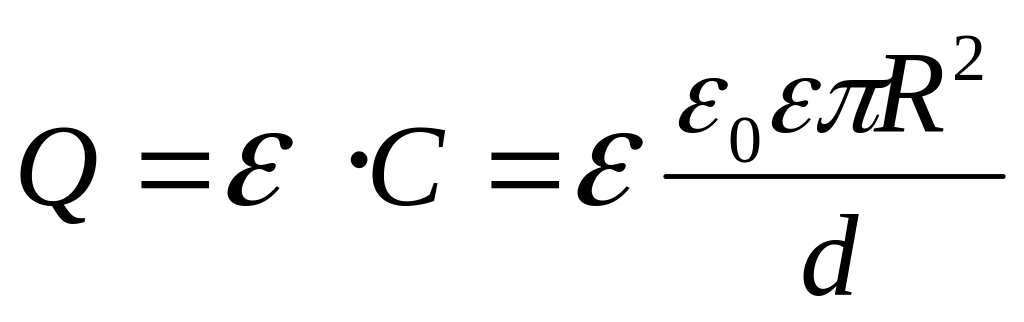 , (3)
, (3)
Для однорідного поля (поля плоского конденсатора) напруженість дорівнює
![]() ,
(4)
,
(4)
де — різниця потенціалів між пластинами конденсатора; d — відстань між ними.
Зробимо підстановку заданих в умові величин у системі СІ у вирази (3) та (4) і отримаємо відповідь:
Q = Е =
3.116. Дві металеві кульки радіусами R1 = 5 см і R2 = 10 см мають заряди Q1 = 40 нКл і Q2 = - 20 нКл, відповідно. Знайти енергію W яка виділиться при з'єднанні куль провідником.
3.116.
Дано
R1
= 5 см R2
= 10 см Q1
= 40 нКл Q2
= - 20 нКл
= ?
Енергію W яка виділиться при з'єднанні куль провідником дорівнюватиме різниці енергій куль до і після з’єднання їх провідником:
![]() . (1)
. (1)
Електрична енергія відокремленого зарядженого провідника
. (2)
Ємність провідної кулі радіуса г
![]() . (3)
. (3)
Тоді енергія куль до з’єднання дорівнює
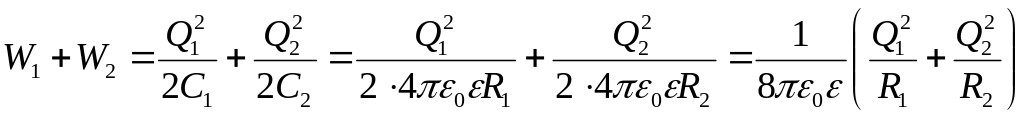 . (4)
. (4)
При з’єднанні куль провідником заряди будуть переміщатися доки потенціали куль не зрівняються, тоді нові заряди куль можна визначити за формулами:
![]() . (5)
. (5)
А сумарний заряд куль після з’єднання дорівнюватиме
![]() . (6)
. (6)
З рівнянь (5) та (6) можна визначити заряди куль після їхнього з’єднання:
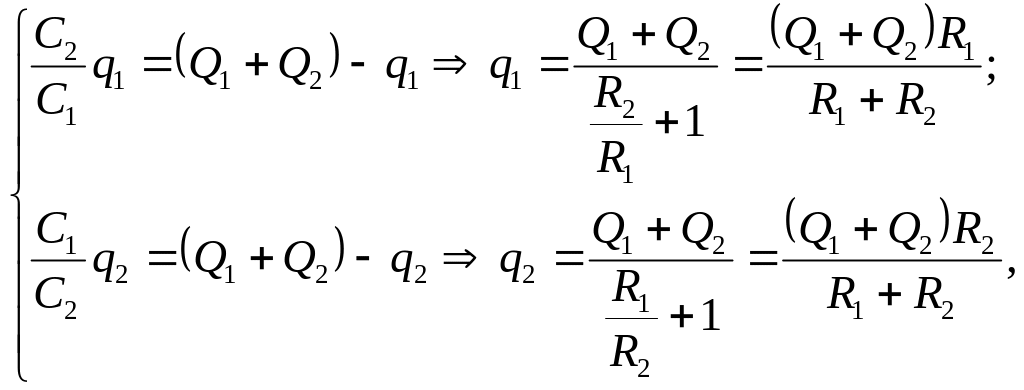 (7)
(7)
тоді енергія електричного поля куль після їхнього з’єднання дорівнюватиме
 . (8)
. (8)
Енергії з виразів (4) та (8) підставляємо в формулу (1) і отримаємо вираз для розрахунку відповіді:
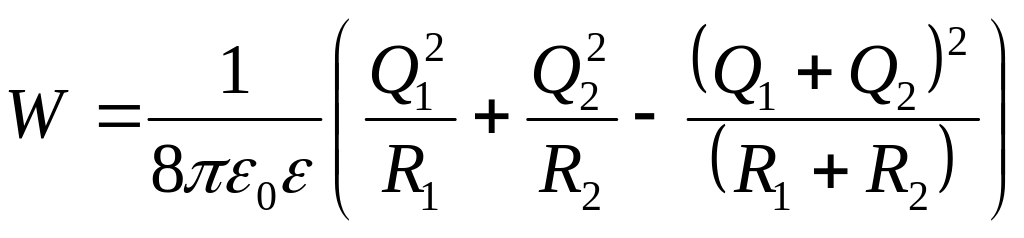 . (8)
. (8)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (8) і отримаємо відповідь:
=
3.117. Простір між
пластинами плоского конденсатора
заповнено двома шарами діелектрика:
скла (![]() = 6) товщиною d1
= 0,2 см і шаром парафіну (
= 6) товщиною d1
= 0,2 см і шаром парафіну (![]() = 2) товщиною d2
= 0,3 см. Різниця потенціалів між обкладками
= 300 В. Визначити напруженість Е
поля і падіння потенціалу в кожному із
шарів.
= 2) товщиною d2
= 0,3 см. Різниця потенціалів між обкладками
= 300 В. Визначити напруженість Е
поля і падіння потенціалу в кожному із
шарів.
3.117.
Дано
d1
= 0,2 см
= 6 d2
= 0,3 см
= 2
= 300 В
![]() = ?
= ?
![]() = ?
= ?![]() = ?
= ?
![]() = ?
= ?
Щоб знайти величини
![]() ,
,
![]() ,
з'ясуємо зв'язок, що існує між ними і
різницею потенціалів
.
Скористаємося формулою зв’язку
між потенціалом і напруженістю поля.
Тобто градієнт потенціалу
дорівнює
напруженості поля
,
з'ясуємо зв'язок, що існує між ними і
різницею потенціалів
.
Скористаємося формулою зв’язку
між потенціалом і напруженістю поля.
Тобто градієнт потенціалу
дорівнює
напруженості поля
![]() .
(1)
.
(1)
Зв’язок між напруженістю та потенціалом поля:
. (2)
Звідки різниця потенціалів двох точок поля дорівнює
. (3)
Для однорідного поля (поля плоского конденсатора) напруженість
![]() ,
(4)
,
(4)
де U — різниця потенціалів між пластинами конденсатора; d — відстань між ними.
Розбивши весь шлях інтегрування на дві частини, які відповідні товщині двох шарів діелектриків (товщиною зазору нехтуємо), і враховуючи, що в межах кожного шару поле однорідне, отримаємо
![]() .
(5)
.
(5)
Так як електричний
зсув
![]() в обох шарах діелектриків має одне і те
ж значення, то скорочуючи на
запишемо:
в обох шарах діелектриків має одне і те
ж значення, то скорочуючи на
запишемо:
![]() .
(6)
.
(6)
Вирішуючи спільно рівняння (5) і (6), одержимо:
![]() ;
;
![]() . (7)
. (7)
З формули (5) можна отримати падіння потенціалу в кожному із шарів:
![]() .
(8)
.
(8)
Зробимо підстановку заданих в умові величин у системі СІ у вирази (7) та (8) і отримаємо відповіді:
= = = =
` 3.118. Плоский конденсатор з площею пластин S = 200 см2 кожна, заряджений до різниці потенціалів = 2 кВ. Відстань між пластинами d = 2 см. Діелектрик – скло ( = 6). Визначити енергію W конденсатора та її густину ω.
3.118.
Дано
S
= 200 см2
= 2 кВ
= 2 см
= 6
W = ? ω
= ?
Електрична енергія відокремленого зарядженого провідника ємністю і потенціалом дорівнює
![]() . (1)
. (1)
Для плоского конденсатора електрична ємність дорівнює
(2)
тоді енергію можна визначити за формулами:
![]() , (3)
, (3)
Об'ємна густина енергії електричного поля
![]() , (4)
, (4)
де
![]() - електричне зміщення, Кл/м2.
— об'єм,
обмежений пластинами конденсатора.
- електричне зміщення, Кл/м2.
— об'єм,
обмежений пластинами конденсатора.
Зробимо підстановку заданих в умові величин у системі СІ у вирази (3) та (4) і отримаємо відповіді:
W = ω =
3.119. Конденсатори ємністю С1 = 5 мкФ і С2 = 10 мкФ заряджені до напруги U1 = 60 В и U2 = 100 В, відповідно. Визначити напругу на обкладках конденсаторів після їхнього з'єднання обкладками; що мають однойменні заряди.
3.119.
Дано
U1
= 60 В U2
= 100 В С1
= 5 мкФ С2
= 10 мкФ
= ?
Рис. 3.119
Згідно закону збереження кількості заряду можна стверджувати, що заряд на батареї конденсаторів дорівнює сумі зарядів на кожному з них
. (1)
Визначити напругу на обкладках конденсаторів після їхнього з'єднання обкладками, що мають однойменні заряди, можна за формулою
. (2)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (2) та отримаємо відповідь:
=
3.120. Скільки витків ніхромового дроту діаметром = 1 мм треба навити на фарфоровий циліндр радіусом = 2,5 см, щоб отримати опір у = 40 Ом?
3.120.
Дано
= 1 мм
= 2,5 см
= 40 Ом
![]() = ?
= ?
Кількість витків визначимо як відношення довжин дроту та одного витка:
![]() . (1)
. (1)
Опір циліндричного провідника довжиною та площею поперечного перерізу
![]() , (2)
, (2)
де
![]() — питомий опір.
— питомий опір.
Довжину дроту визначаємо з формули (2) та підставляємо у (1) і получаємо вираз для розрахунку кількості витків:
= (3)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (3) та отримаємо відповідь:
=
3.121. Резистор з опором R1 = 5 Ом, вольтметр і джерело струму з'єднані паралельно. Вольтметр показує напруга U1 = 10 В. Якщо замінити резистор іншим з опором R2 = 12 Ом, то вольтметр покаже напруга U2 = 12 В: Визначити е.р.с. і внутрішній опір джерела струму.
3.121.
Рис. 3.121
Дано
R1
= 5 Ом
U1
= 10 В R2
= 120 Ом U2
= 12 В
= ?
= ?
Закон Ома для повного електричного кола має вигляд:
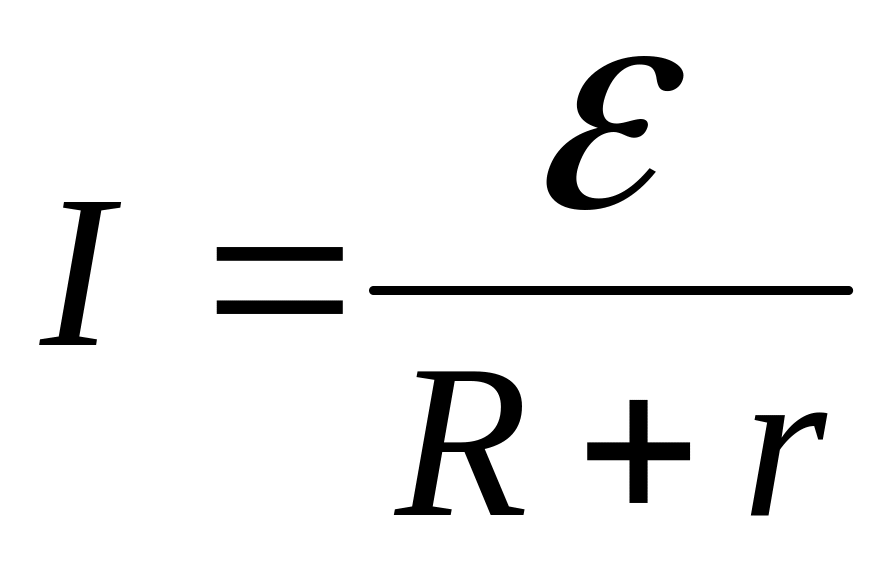 , (1)
, (1)
де — зовнішній опір; — внутрішній опір кола.
Запишемо формулу цього закону для двох випадків підключення опорів:
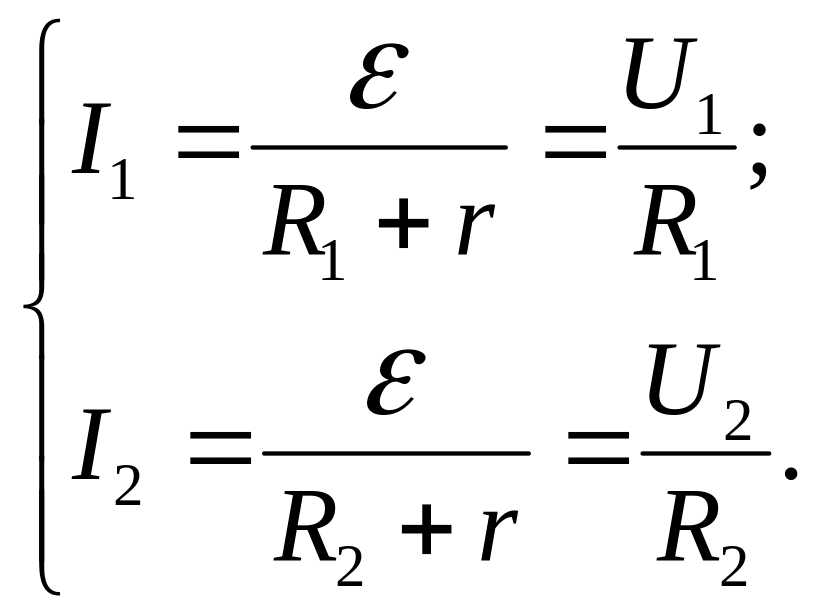 . (2)
. (2)
Знаходимо відношення першого рівняння системи (2) до другого і отримаємо вираз для розрахунку внутрішнього опору джерела струму:
 , (3)
, (3)
З любого рівняння системи (3), наприклад, другого, визначаємо електрорушійну силу джерела струму і підставляємо в одержану формулу значення внутрішнього опору джерела струму :
![]() = (4)
= (4)
Зробимо підстановку заданих в умові величин у системі СІ у вирази (3) та (4) отримаємо відповіді:
= =
3.122. Визначити електричний заряд, що пройшов за = 20 секунд крізь поперечний переріз проводу з опором R = 3 Ом при рівномірному наростанні напруги на його кінцях від U1 = 2 В до U2 = 4 В.
3.122.
Дано
= 20 с
R
= 3 Ом U1
= 2 В U2
= 4 В
= ?
Сила електричного струму чисельно дорівнює зміні заряду, перенесеного через поперечний переріз провідника, залежно від часу
![]() . (1)
. (1)
Звідки можна отримати вираз для визначення електричного заряду, що проходить через перетин провідника за заданий час:
Рис. 3.122![]()

Для визначення рівняння зміни напруги на кінцях проводу, побудуємо графік цієї залежності (див рис. 3.122):
![]() . (2)
. (2)
Підставляємо рівняння напруги з (2) під знак інтеграла
. (3)
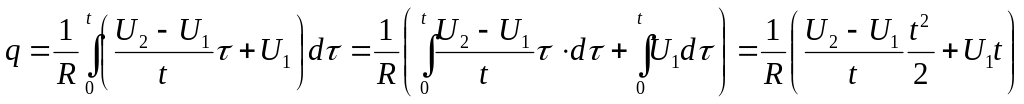 . (4)
. (4)
Зробимо підстановку заданих в умові величин у системі СІ у вираз (4) та отримаємо відповідь:
=
3.123. Визначити силу
струму в електричному колі, що складається
з двох джерел живлення з'єднаних
однойменними полюсами, з е.р.с.
![]() = 1,6 В та
= 1,6 В та
![]() = 1,2 В. їх внутрішній опір r1
= 0,6 Ом, r2
= 0,4 Ом.
= 1,2 В. їх внутрішній опір r1
= 0,6 Ом, r2
= 0,4 Ом.
3.123.
Дано
= 1,6 В
= 1,2 В r1
= 0,6 Ом r2
= 0,4 Ом
Рис. 3.123
![]() = ?
= ?
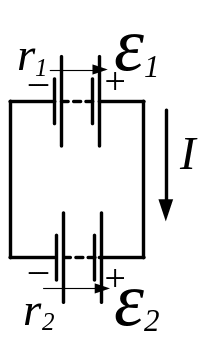
Зробимо малюнок, на який наносимо напрямок току та електрорушійної сили в кожному джерелі струму. Вибираємо обхід контуру проти годинникової стрілки і записуємо формулу другого закону Кірхгофа:
![]() . (1)
. (1)
З рівняння (1) отримаємо вираз для розрахунку силу струму в електричному колі:
= (2)
Зробимо підстановку заданих в умові величин у вираз (2) та отримаємо відповідь:
=
3.124. Гальванічний
елемент дає на зовнішній опір у
![]() = 0,5 Ом силу струму
= 0,5 Ом силу струму
![]() = 0,2 А. Якщо зовнішній опір замінити на
R2
= 0,8 Ом, то елемент дає силу струму І2
= 0,15 А. Визначити силу струму короткого
замикання.
= 0,2 А. Якщо зовнішній опір замінити на
R2
= 0,8 Ом, то елемент дає силу струму І2
= 0,15 А. Визначити силу струму короткого
замикання.
3.124.
Рис. 3.124
Дано
= 0,5 Ом
= 0,2 А R2
= 0,8 Ом І2
= 0,15 А

![]() = ?
= ?
Зробимо малюнок.
Закон Ома для повного кола має вигляд:
, (1)
де — зовнішній опір; — внутрішній опір.
З рівняння (1) можна зробити висновок, що струм короткого замикання отримаємо, якщо зовнішній опір кола дорівнюватиме нулю:
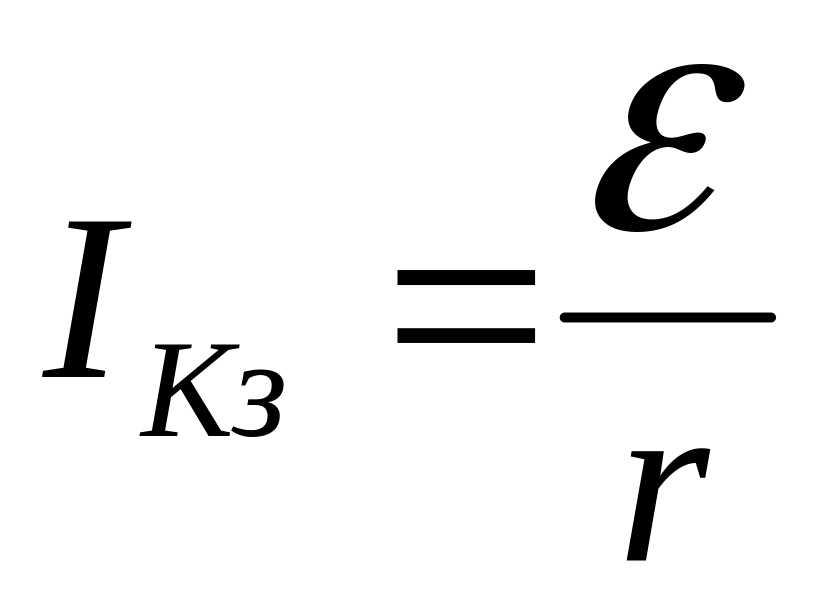 , (2)
, (2)
Для визначення параметрів джерела струму: електрорушійної сили і внутрішнього опору, складемо систему рівнянь з формули закону Ома для двох випадків підключення зовнішнього опору:
 , (3)
, (3)
Для визначення внутрішнього опору джерела струму, знайдемо відношення першого рівняння системи (1) до другого:
![]() . (4)
. (4)
Значення опору підставляємо в одне із рівнянь системи (3) і отримаємо е.р.с. джерела струму:
![]() . (5)
. (5)
Підставляємо з рівняння (4) та з рівняння (5) в рівняння (2) і отримаємо вираз для розрахунку :
= (6)
Зробимо підстановку заданих в умові величин у вираз (6) та отримаємо відповідь:
=
3.125. До джерела струму з е.р.с. = 12 В приєднали зовнішнє навантаження. Напруга на клемах джерела стала при цьому рівною U = 8 В. Визначити у відсотках к.к.д. джерела струму.
3.125.
Дано
= 12 В
U
= 8 В
![]() = ?
= ?
Відношення корисної потужності до загальної потужності визначає ККД джерела струму
![]() . (1)
. (1)
Помножимо чисельник і знаменник рівняння (1) на струм і, користуючісь формулою закону Ома отримаємо вираз для розрахунку к.к.д.:
![]() . (2)
. (2)
Зробимо підстановку заданих в умові величин у вираз (2) та отримаємо відповідь:
=
3.126. Зовнішня ділянка електричного кола споживає потужність Р = 0,75 Вт. Визначити силу струму в мережі, якщо е.р.с. джерела струму становить = 2 В, а його внутрішній опір r = 1 Ом.
3.126.
Дано
= 2 В
r
= 1 Ом Р
= 0,75 Вт
![]() = ?
= ?
З закону Ома для повного кола можна отримати
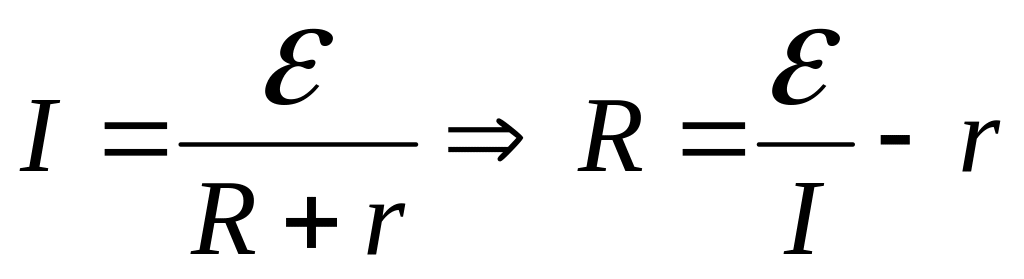 , (1)
, (1)
де — зовнішній опір; — внутрішній опір.
Потужність чисельно дорівнює роботі постійного струму за одиницю часу, тому отримаємо з формули потужності зовнішній опір:
![]() .
(2)
.
(2)
З рівнянь (1) та (2) отримаємо квадратне рівняння
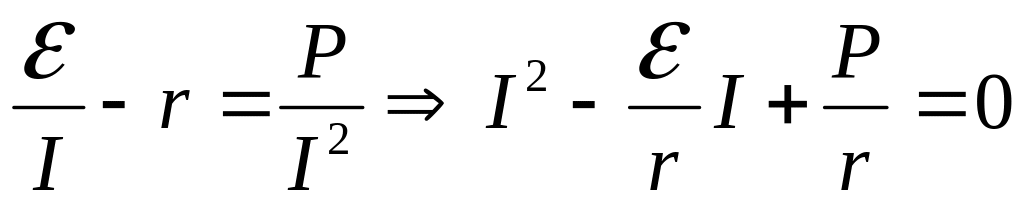 , (3)
, (3)
Розв’язок якого і є виразом для розрахунку струму:
= (4)
Зробимо підстановку заданих в умові величин у вираз (4) та отримаємо відповідь:
=
3.127. Сила струму в провіднику змінюється з часом за законом І = 4 + 2t2. Який заряд проходить через поперечний перетин провідника за проміжок часу від t1 = 2 с до t2 = 6 с?
3.127.
Дано
І
= 4 + 2t2 t1
= 2 с
t2
= 6 с
= ?
Сила електричного струму чисельно дорівнює зміні заряду, перенесеного через поперечний переріз провідника, залежно від часу
. (1)
Звідки можна отримати вираз для визначення електричного заряду, що проходить через перетин провідника за заданий час:
 .
(2)
.
(2)
Зробимо підстановку заданих в умові величин у вираз (2) та отримаємо відповідь:
=
3.128. Сила струму в провіднику з опором R = 10 Ом за час t = 50 с рівномірно наростає від I1 = 5 А до І2 = 10 А. Визначити кількість теплоти Q, що виділилося за цей час у провіднику.
3.128.
Дано
R
= 10 Ом
t
= 50 с I1
= 5 А
І2
= 10 А
= ?
Рис. 3.128
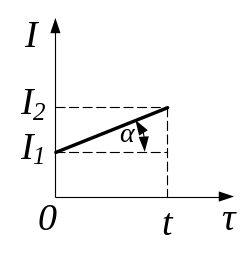
Кількість теплоти
![]() ,
що виділяється в провіднику при
проходженні в ньому постійного струму
(закон Джоуля — Ленца),
,
що виділяється в провіднику при
проходженні в ньому постійного струму
(закон Джоуля — Ленца),
![]() . (1)
. (1)
З рис. 3.128 видно, що рівняння цього графіку буде пряма
![]() . (2)
. (2)
З виразу (1) інтегруванням можна отримати вираз для визначення кількості теплоти, що виділиться в провіднику за заданий час:
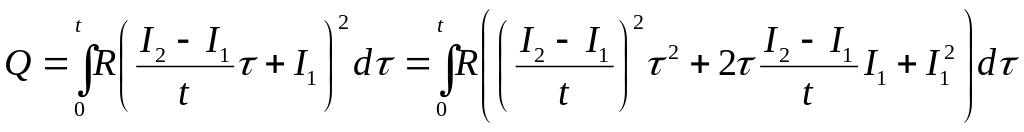 .
.
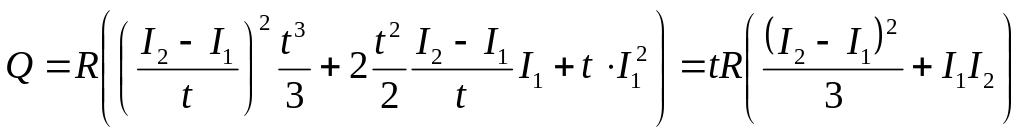 . (3)
. (3)
Зробимо підстановку заданих в умові величин у вираз (3) та отримаємо відповідь:
=
3.129. При рівномірному зростанні сили струму у провіднику від I1 = 1 А до І2 = 2 А за t = 10 секунд виділилася кількість теплоти Q = 5 кДж. Знайти опір R провідника.
3.129.
Дано
I1
= 1 А І2
= 2 А t
= 10 с Q
= 5 кДж
= ?
Рис. 3.129
Кількість теплоти , що виділяється в провіднику при проходженні в ньому постійного струму (закон Джоуля — Ленца),
. (1)
З рис. 3.129 видно, що рівняння цього графіку буде пряма
. (2)
З виразу (1) інтегруванням можна отримати вираз для визначення кількості теплоти, що виділиться в провіднику за заданий час:
.
. (3)
Звідки отримаємо вираз для розрахунку опору
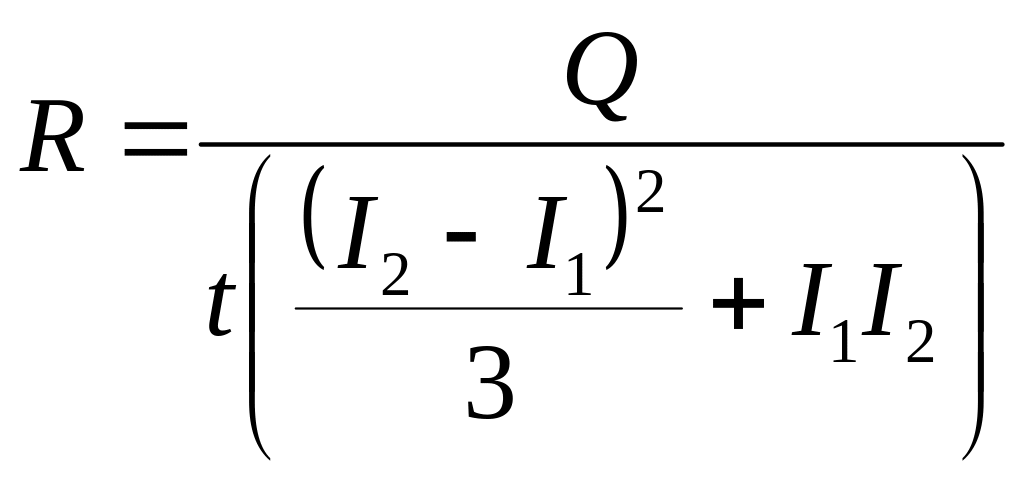 . (4)
. (4)
Зробимо підстановку заданих в умові величин у вираз (4) та отримаємо відповідь:
=
3.130. Який об'єм води
можна закип'ятити, затративши електричну
енергію Q
= 3 ГВт-г? Початкова температура води
![]() = 10°С.
= 10°С.
3.130.
Дано
Q
= 3∙3600∙109
Дж
= 10°С
= ?
![]() = 1000 кг/м3
= 1000 кг/м3
![]() = 4190 Дж/(кг∙К)
= 4190 Дж/(кг∙К)
Енергія, яка необхідна для нагрівання води визначається за формулою
![]() ,
(1)
,
(1)
де - питома теплоємність.
З формули (1) знаходимо який об'єм води можна закип'ятити
![]() .
(2)
.
(2)
Зробимо підстановку заданих в умові величин у вираз (2) та отримаємо відповідь:
=
3.131. На плитці
потужністю
![]() = 0,5 кВт стоїть чайник, в який налитий
= 1 літр води при температурі
= 16°С. Вода в чайнику закипіла через
=20 хвилин після вмикання плитки. Яка
кількість теплоти Q
при цьому втрачена на нагрівання повітря.
= 0,5 кВт стоїть чайник, в який налитий
= 1 літр води при температурі
= 16°С. Вода в чайнику закипіла через
=20 хвилин після вмикання плитки. Яка
кількість теплоти Q
при цьому втрачена на нагрівання повітря.
3.131.
Дано
= 0,5 кВт
= 1 л
= 16°С
=20 хв
= 1000 кг/м3
= 4190 Дж/(кг∙К)
![]() = ?
= ?
Енергія, яка необхідна для нагрівання води визначається за формулою
![]() ,
(1)
,
(1)
де - питома теплоємність.
Витрачена електрична енергія дорівнює
![]() .
(2)
.
(2)
Кількість теплоти, яка при цьому втрачена на нагрівання повітря
![]() .
(3)
.
(3)
Зробимо підстановку заданих в умові величин у системі одиниць СІ у вираз (3) та отримаємо відповідь:
=
3.132. = 4,5 літра води можна закип'ятити, затративши електричну енергію Q = 0,5 кВт-г. Початкова температура води = 23°С. Знайти к.к.д. нагрівника.
3.132.
Дано
Q
= 0,5 кВт-г
= 4,5 л
= 23°С
= 1000 кг/м3
= 4190 Дж/(кг∙К)
= ?
Енергія, яка необхідна для нагрівання води визначається за формулою
![]() ,
(1)
,
(1)
де - питома теплоємність.
Тоді к.к.д. дорівнює
![]() .
(2)
.
(2)
Зробимо підстановку заданих в умові величин у системі одиниць СІ у вираз (2) та отримаємо відповідь:
=
3.133. Температура водяного термостата об'ємом = 1 літр підтримується постійною за допомогою нагрівника потужністю = 26 Вт. На нагрівання води витрачається = 80% цієї потужності. На скільки знизиться температура води в термостаті за = 10 хвилин, якщо нагрівник вимкнути?
3.133.
Дано
= 1 л
= 26 Вт
= 80%
= 10 хв
= 1000 кг/м3
= 4190 Дж/(кг∙К)
![]() = ?
= ?
Енергія, яка необхідна для нагрівання води визначається за формулою
![]() ,
(1)
,
(1)
де - питома теплоємність.
Тоді к.к.д. дорівнює
![]() .
(2)
.
(2)
З формули (2) отримуємо
![]() .
(2)
.
(2)
Зробимо підстановку заданих в умові величин у системі одиниць СІ у вираз (2) та отримаємо відповідь:
=
3.134. Вольфрамова
нитка електричної лампочки при температурі
![]() = 20°С має опір R1
= 35,8 Ом. Яка буде температура нитки, якщо
при вмиканні лампочки в мережу напругою
= 120 В по ній йде струм
= 0,33 А? Температурний коефіцієнт опору
вольфраму α
=4,6 10-3
К-1.
= 20°С має опір R1
= 35,8 Ом. Яка буде температура нитки, якщо
при вмиканні лампочки в мережу напругою
= 120 В по ній йде струм
= 0,33 А? Температурний коефіцієнт опору
вольфраму α
=4,6 10-3
К-1.
3.134.
Дано
= 20°С
R1
= 35,8 Ом
= 120 В
= 0,33 А α
=4,6 10-3
К-1
![]() = ?
= ?
Питомий опір провідника залежить від його температури
![]() , (1)
, (1)
де
![]() — питомий опір при 0°С;
— питомий опір при 0°С;
![]() — температурний коефіцієнт опору.
— температурний коефіцієнт опору.
Якщо знехтувати зміною розмірів провідника при зміні його температури, то можна записати, для двох температур провідника, значення їхніх опорів:
![]() , (2)
, (2)
де
![]() - опір провідника при 0°С.
- опір провідника при 0°С.
Опір провідника в другому випадку знайдемо за законом Ома, тобто за формулою:
![]() . (3)
. (3)
Підставляємо опір з виразу (3) у систему рівнянь (2) і знайдемо з відношення цих рівнянь шукану температуру
![]() , (4)
, (4)
Зробимо підстановку заданих в умові величин у вираз (4) та отримаємо відповідь:
=
3.135. Обмотка котушки
з мідного дроту при температурі
= 14°С має опір
= 10 Ом. Після проходження струму, опір
обмотки став рівним
= 12,2 Ом. До якої температури
![]() нагрілася обмотка? Температурний
коефіцієнт опору міді α = 4,15 10-3
К-1.
нагрілася обмотка? Температурний
коефіцієнт опору міді α = 4,15 10-3
К-1.
3.135.
Дано
= 14°С
= 10 Ом
= 12,2 Ом α
= 4,15 10-3
К-1
= ?
Питомий опір провідника залежить від його температури
, (1)
де — питомий опір при 0°С; — температурний коефіцієнт опору.
Якщо знехтувати зміною розмірів провідника при зміні його температури, то можна записати, для двох температур провідника, значення їхніх опорів:
, (2)
де - опір провідника при 0°С.
З відношення рівнянь системи (2) знайдемо шукану температуру
![]() , (3)
, (3)
Зробимо підстановку заданих в умові величин у вираз (3) та отримаємо відповідь:
=
3.136. Яку частку е.р.с. елемента живлення складає різниця потенціалів U на його клемах, якщо внутрішній опір елемента r в 10 разів менший зовнішнього опору R.
3.136.
Дано
![]()
![]() = ?
= ?
Відношення корисної потужності до загальної потужності визначає ККД джерела струму
. (1)
Помножимо чисельник і знаменник рівняння (1) на струм і, користуючись формулою закону Ома отримаємо вираз для розрахунку к.к.д.:
. (2)
Зробимо підстановку заданих в умові величин у вираз (2) та отримаємо відповідь:
=
3.137. Від батареї, е.р.с. якої = 600 В, потрібно передати енергію на відстань = 1 км. Потужність, що споживається = 5 кВт. Знайти мінімальні втрати потужності в мережі, якщо діаметр мідних проводів, що використовуються = 0,5 см.
3.137.
Дано
= 600 В
= 1 км
= 5 кВт
= 0,5 см
![]() = ?
= ?
Втрати потужності в мережі визначаємо за формулою
![]() , (1)
, (1)
де
![]() - повна потужність всієї мережі;
- струм у мережі;
- повна потужність всієї мережі;
- струм у мережі;
![]() опір двох провідної мережі;
= 1,7∙10-8
Ом∙м – питомий опір.
опір двох провідної мережі;
= 1,7∙10-8
Ом∙м – питомий опір.
З рівняння (1) складемо квадратне рівняння
![]() , (2)
, (2)
Рішення якого матиме вигляд
![]() , (3)
, (3)
мінімальний струм знаходимо за формулою:
![]() , (4)
, (4)
У формулу втрати потужності в мережі підставляємо значення струму з формули (4):
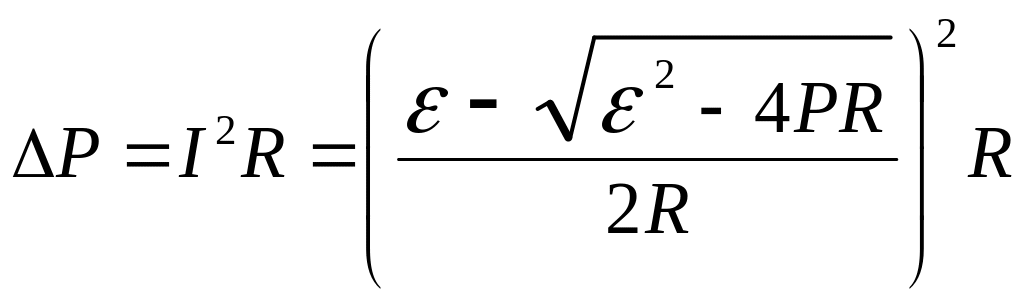 , (5)
, (5)
Зробимо підстановку заданих в умові величин у вираз (2) та отримаємо відповідь:
=
3.138. При зовнішньому опорі R1 = 8 Ом сила струму в електричному колі I1 = 0,8 А, при опорі R2 = 15 Ом сила струму І2 = 0,5 А. Визначити силу струму короткого замикання.
3.138.
Рис. 3.138
Дано
= 8 Ом
= 0,8 А R2
= 15 Ом І2
= 0,5 А
= ?
Зробимо малюнок.
Закон Ома для повного кола має вигляд:
, (1)
де — зовнішній опір; — внутрішній опір.
З рівняння (1) можна зробити висновок, що струм короткого замикання отримаємо, якщо зовнішній опір кола дорівнюватиме нулю:
, (2)
Для визначення параметрів джерела струму: електрорушійної сили і внутрішнього опору, складемо систему рівнянь з формули закону Ома для двох випадків підключення зовнішнього опору:
, (3)
Для визначення внутрішнього опору джерела струму, знайдемо відношення першого рівняння системи (1) до другого:
. (4)
Значення опору підставляємо в одне із рівнянь системи (3) і отримаємо е.р.с. джерела струму:
. (5)
Підставляємо з рівняння (4) та з рівняння (5) в рівняння (2) і отримаємо вираз для розрахунку :
= (6)
Зробимо підстановку заданих в умові величин у вираз (6) та отримаємо відповідь:
=
3.139. Два паралельно з'єднаних елемента живлення з однаковими е.р.с. у = 2 В і внутрішніми опорами r1 = 1 Ом та r2 = 1,5 Ом, замкнені на зовнішній опір R = 1,4 Ом. Знайти струм І в кожному з елементів живлення.
Рис. 3.139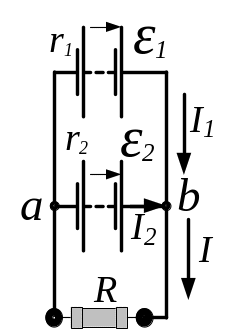
3.139.
Дано
= 2 В r1
= 1 Ом
r2
= 1,5 Ом R
= 1,4 Ом
![]() = ?
= ?
![]() = ?
= ?
Правила Кірхгофа для розгалужених кіл
1. Алгебраїчна сума всіх сил струмів, що сходяться у вузлі розгалуженого кола, дорівнює нулю:
![]() . (1)
. (1)
Струми, що входять у вузол, вважають додатними, які виходять — від'ємними, або навпаки.
2. У будь-якому простому замкненому контурі, довільно обраному у розгалуженому електричному колі, алгебраїчна сума добутків сил струмів на опори відповідних ділянок цього контуру дорівнює алгебраїчній сумі електрорушійних сил, що діють у ньому
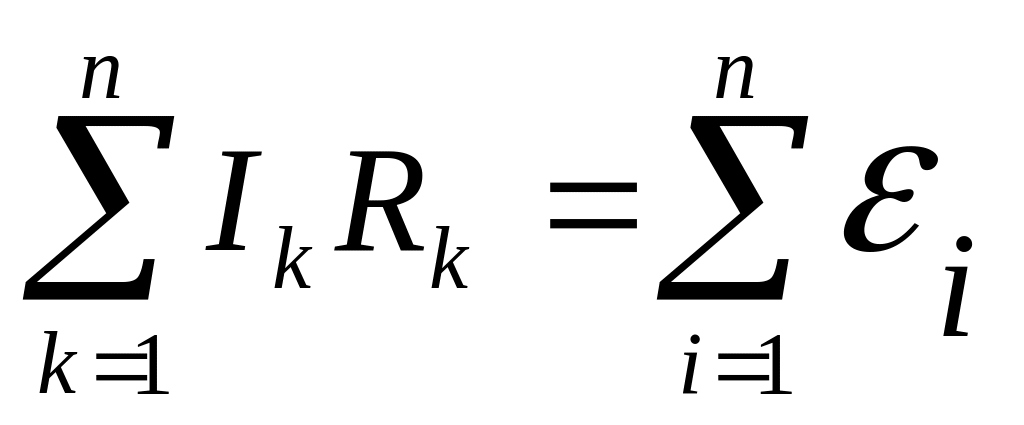 . (2)
. (2)
Для вузла
та для замкнених контурів
![]() і
і
![]() запишемо правила Кірхгофа:
запишемо правила Кірхгофа:
![]() (3)
(3)
Рішення знаходимо за формулами (метод Крамера):
![]() ,
,
![]() ,
,
![]() ,
(4)
,
(4)
де детермінанти дорівнюють:
системи ![]() ; (5)
; (5)
невідомого
![]() ; (6)
; (6)
невідомого
![]() ;
(7)
;
(7)
невідомого
![]() .
(8)
.
(8)
Тоді струми та , знайдемо за формулами (4):
= =
Напруга на клемах елемента живлення = 2,1 В, опори R1 = 5 Ом, R2 = 6 Ом, R3 = 3 Ом (див. рис, 3.140). Який струм І показує амперметр?
3.140.
Рис. 3.140
Дано
= 2,1 В
= 5 Ом
R2
= 6 Ом R3
= 3 Ом
= ?
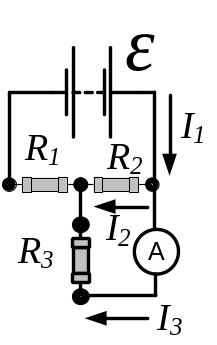
За законом Ома для повного кола, нехтуючи внутрішнім опором джерела струму, можна записати рівняння:
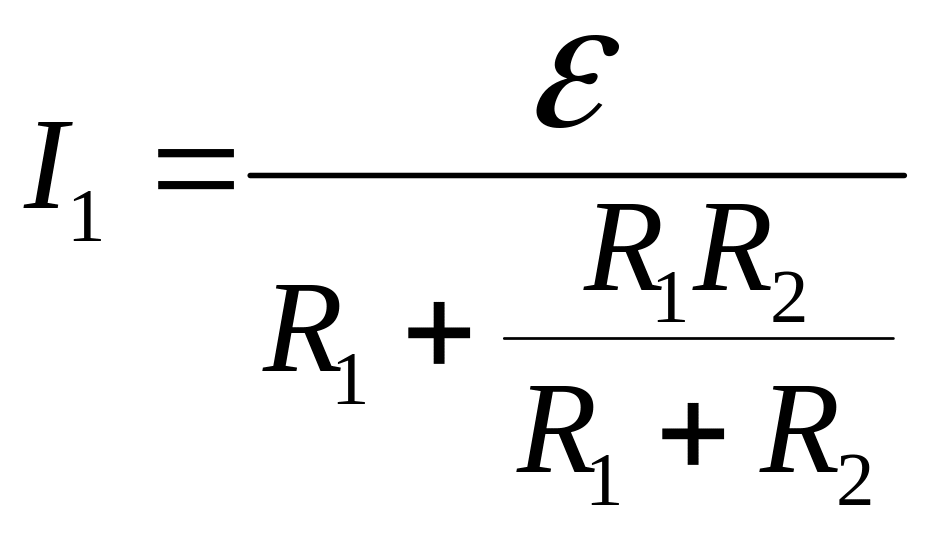 . (1)
. (1)
Тоді напруга на
опорах
![]() та
та
![]() дорівнюватиме
дорівнюватиме
![]() . (2)
. (2)
Визначаємо струм, який показує амперметр
![]() . (3)
. (3)
Зробимо підстановку заданих в умові величин у вираз (3) та отримаємо відповідь:
=
3.141. Елемент живлення, опір і амперметр з'єднані послідовно. Елемент має е.р.с. = 2 В і внутрішній опір = 0,4 Ом. Амперметр показує струм І = 1 А. З яким к.к.д. працює елемент?
3.141.
Дано
= 2 В
= 0,4 Ом І
= 1 А
= ?
Відношення корисної потужності до загальної потужності визначає ККД джерела струму
. (1)
За законом Ома для повного кода можна отримати зовнішній опір:
![]() . (2)
. (2)
Отриманий опір з рівняння (2) підставляємо в формулу (1) і отримаємо вираз для росрахунку к.к.д.:
= (3)
Зробимо підстановку заданих в умові величин у вираз (3) та отримаємо відповідь:
=
Е.р.с. батареї живлення = 100 В, опори R1 = R2 = 40 Ом, R3 = 80 Ом і R4 = 34 Ом. (див. рис. 3.142). Знайти струм I2 що йде через опір R2 і падіння потенціалу U2 на ньому.
3.142.
Рис. 3.142
Дано
= 100 В R1
= R2
= 40 Ом R3
= 80 Ом
R4
= 34 Ом
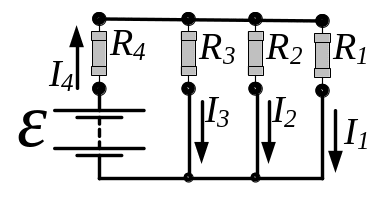
![]() = ? U2
= ?
= ? U2
= ?
За законом Ома для повного кола, нехтуючи внутрішнім опором джерела струму, можна записати рівняння:
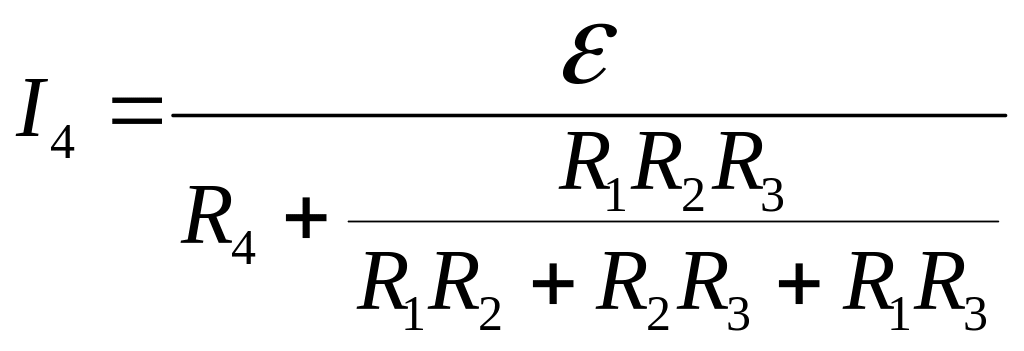 .
(1)
.
(1)
Тоді напруга на опорах , та дорівнюватиме
![]() . (2)
. (2)
Визначаємо струм, який йде через другий опір
![]() . (3)
. (3)
Зробимо підстановку заданих в умові величин у вирази (3) та (2) і отримаємо відповіді:
= U2 =
Е.р.с. батареї живлення = 120 В, опори R3 = 20 Ом, R4 = 25 Ом (див. рис.3.143). Падіння потенціалу на опорі R1 дорівнює = 40 В. Амперметр показує струм
 = 2 А. Знайти
опір R2.
= 2 А. Знайти
опір R2.
3.143.
Рис. 3.143
Дано
= 100 В R3
= 20 Ом,
R4
= 25 Ом
= 40 В
= 2 А

![]() = ?
= ?
За законом Ома для повного кола, нехтуючи внутрішнім опором джерела струму, можна записати рівняння:
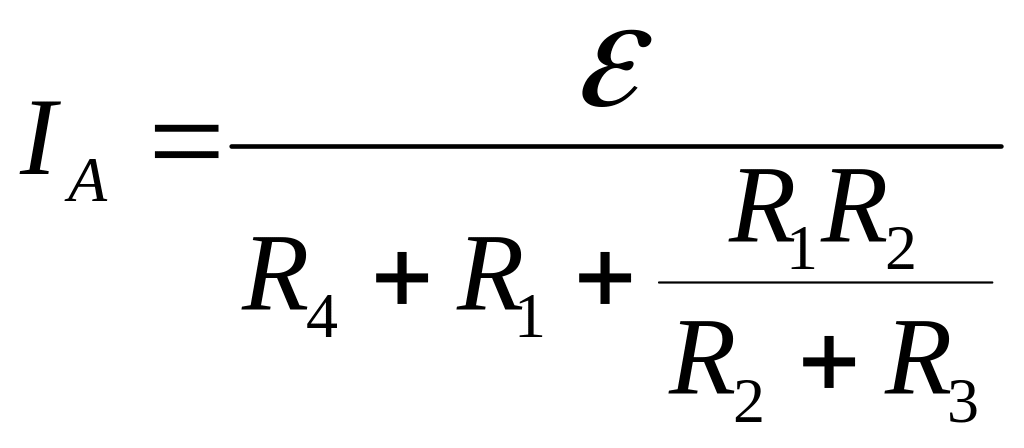 .
(1)
.
(1)
З рівняння (1) визначаємо невідомий опір
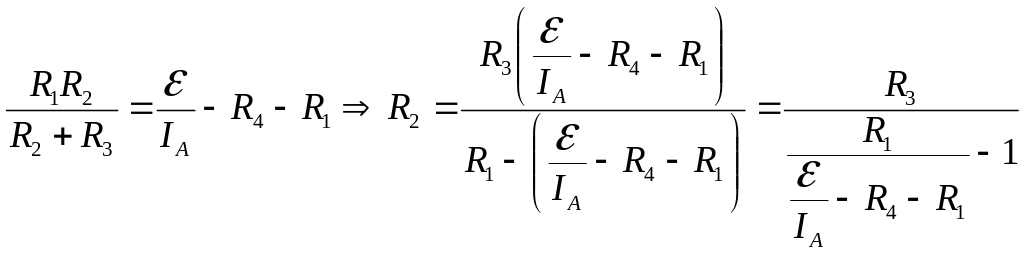 .
(2)
.
(2)
де опір знаходимо за формулою:
![]() . (3)
. (3)
Тоді опор з виразу (3) підставляємо в формулу (2) і отримаємо розрахунковий вираз:
=. (4)
Зробимо підстановку заданих в умові величин у вираз (4) і отримаємо відповіді:
=
Батарея з е.р.с. = 10 В і внутрішнім опором = 1 Ом має к.к.д. η = 0,8 (див. рис. 3.144). Падіння потенціалу на опорах R1 і R4 рівні U1 = 4 В і U4 = 2 В. Яку силу струму показує амперметр? Знайти падіння потенціалу на опорі R2.
3.144.
Рис. 3.144
Дано
= 10 В
= 1 Ом η
= 0,8 U1
= 4 В
U4
= 2 В
= ?
= ?
Відношення корисної потужності до загальної потужності визначає ККД джерела струму
![]() , (1)
, (1)
де
- загальний опір зовнішнього кола;
![]() - падіння напруги на зовнішньому опорі.
- падіння напруги на зовнішньому опорі.
З формули (1) отримуємо
![]() , (2)
, (2)
де
![]() - напруга на другому та третьому опорах.
- напруга на другому та третьому опорах.
За законом Ома для повного кола та за формулою к.к.д. можна записати систему рівнянь:
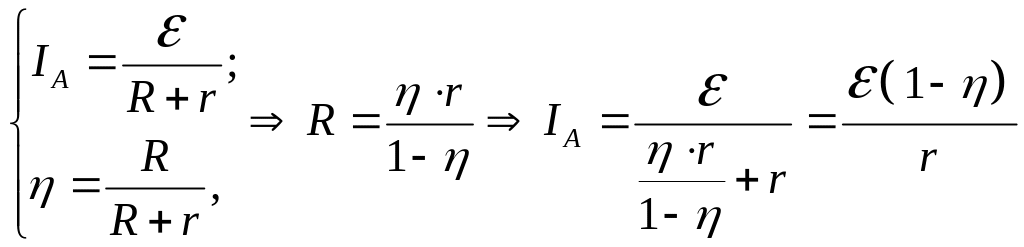 .
(3)
.
(3)
Зробимо підстановку заданих в умові величин у вирази (3) та (2) і отримаємо відповіді:
= =
` 3.145. Е.р.с. батареї = 100 В, опори R1 = 100 Ом, R2 = 200 Ом і R3 = 300 Ом, опір вольтметра RV = 2 кОм (див. рис. 3.145). Яку різницю потенціалів U показує вольтметр?
Рис. 3.145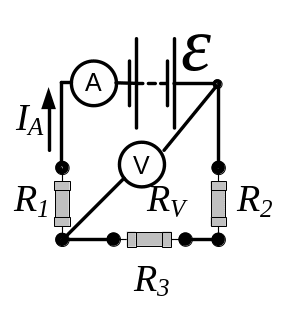
3.145.
Дано
= 100 В R1
= 100 Ом,
R2
= 200 Ом
R3
= 300 Ом,
RV
= 2 кОм
= ?
За законом Ома для повного кола, нехтуючи внутрішнім опором джерела струму, можна записати рівняння:
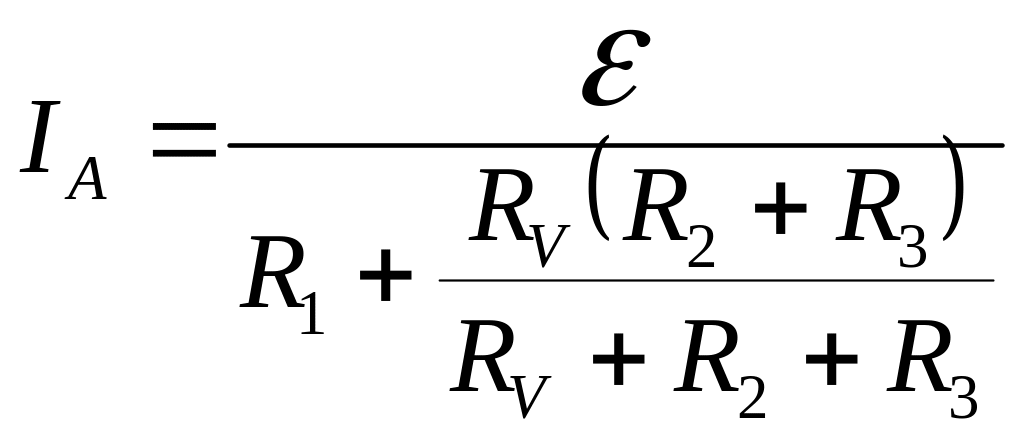 .
(1)
.
(1)
Тоді вольтметр показує напругу
![]() .
(2)
.
(2)
Струм з формули (1) підставляємо у формулу (2) і отримаємо вираз для розрахунку різниці потенціалів U, яку показує вольтметр:
= (3)
Зробимо підстановку заданих в умові величин у вираз (3) і отримаємо відповіді:
=
Опори R1 = R2 = R3 = 200 Ом, опір вольтметра RV = 2 кОм (див рис. 3.146). Вольтметр показує різницю потенціалів U = 100 В. Знайти е.р.с. батареї живлення.
3
Рис. 3.146
Дано
R1
= 200 Ом,
R2
= 200 Ом
R3
= 200 Ом,
RV
= 2 кОм U
= 100 В
= ?
За законом Ома для повного кола, нехтуючи внутрішнім опором джерела струму, можна записати рівняння:
. (1)
З другого боку загальний струм дорівнює
![]() .
(2)
.
(2)
3 рівнянь (1) і (2) отримаємо вираз для розрахунку відповіді:
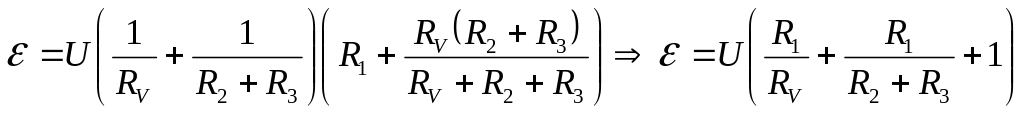 .
(3)
.
(3)
Зробимо підстановку заданих в умові величин у вираз (3) і отримаємо відповіді:
=
3.147. Є = 120-вольтова електрична лампочка потужністю = 40 Вт. Який додатковий опір R треба включити послідовно з лампочкою, щоб вона давала нормальне розжарення при напрузі в мережі U0 = 220 В? Яку довжину ніхромового дроту діаметром = 0,3 мм треба взяти, щоб отримати такий опір?
3.147.
Дано
U
= 120 В
= 40 Вт U0
= 220 В
= 0,3 мм
= ?
=?
Рис. 3.147
Струм в мережі визначимо з потужності лампи:
![]() .
(1)
.
(1)
За законом Ома можна визначити додатковий опір:
![]() .
(2)
.
(2)
Опір циліндричного провідника довжиною та площею поперечного перерізу
![]() , (3)
, (3)
де = 1∙10-6 Ом∙м — питомий опір ніхрому.
Зробимо підстановку заданих в умові величин у вирази (2) та (3) і отримаємо відповіді:
= =
3.148. Від генератора з е.р.с. у = 110 В, потрібно передати енергію на відстань L = 250 м. Потужність, що споживається = 1 кВт. Знайти мінімальний перетин S мідних ( = 1,7∙10-8 Ом∙м) проводів живлення, якщо втрати потужності в мережі не, повинні перевищувати = 1 %.
3.148.
Дано
= 110 В
= 250 м
= 1 кВт
=
/
= 1 %
= ?
Втрати потужності в мережі можна визначити за формулами:
![]() , (1)
, (1)
де
- повна потужність всієї мережі;
- струм у мережі;
![]() опір двох провідної мережі.
опір двох провідної мережі.
З рівняння (1, б) визначаємо струм і підставляємо його в рівняння (1, а)
![]() , (2)
, (2)
Зробимо підстановку заданих в умові величин у вираз (2) та отримаємо відповідь:
=
3.149.
Елемент живлення замикають спочатку
на зовнішній опір
= 2 Ом, а потім на зовнішній опір
= 0,5 Ом. Знайти е.р.с. елемента живлення
і його внутрішній опір r,
якщо відомо, що в кожному з цих випадків
потужність, яка виділяється у зовнішньому
колі, однакова і дорівнює
![]() = 2,54 Вт.
= 2,54 Вт.
3.138.
Рис. 3.138
Дано
= 2 Ом
= 0,5 Ом
= 2,54 Вт
= ?
= ?
Зробимо малюнок.
Потужність чисельно дорівнює роботі постійного струму за одиницю часу
![]() . (1)
. (1)
Користуючись виразом (1) і умовою задачі, складемо рівняння:
![]() . (2)
. (2)
Закон Ома для повного кола має вигляд:
, (3)
де — зовнішній опір; — внутрішній опір.
Для визначення параметрів джерела струму: електрорушійної сили і внутрішнього опору, складемо систему рівнянь з формули закону Ома для двох випадків підключення зовнішнього опору:
, (4)
Для визначення внутрішнього опору джерела струму, знайдемо відношення першого рівняння системи (4) до другого та використаємо формулу (2):
![]() . (5)
. (5)
Значення опору підставляємо в одне із рівнянь системи (3) і отримаємо е.р.с. джерела струму:
![]() . (6)
. (6)
Зробимо підстановку заданих в умові величин у системі одиниць СІ в вирази (6) та (5) і отримаємо відповіді:
= =
3.150. Батареї живлення мають е.р.с. = 2 В та = 4 В, опір R1 = 0,5 Ом (див. рис. 3.150). Падіння потенціалу на опорі R2 дорівнює = 1 В. Знайти, що показує амперметр.
3
3.150
Дано
= 2 В
= 4 В R1
= 0,5 Ом
= 1 В
= ?
