Вопросы к экзамену
Г-512
Определение производной. Геометрический смысл производной.
Правила дифференцирования.
Таблица производных.
Первообразная функция и неопределенный интеграл.
Интегралы от основных элементарных функций.
Понятие интегральной суммы. Геометрический смысл интегральной суммы.
Понятие определенного интеграла. Формула Ньютона-Лейбница.
Замена переменной и формула интегрирования по частям в определенном интеграле.
Матрицы (определение, обозначение, квадратная матрица, диагональная матрица, единичная матрица).
Операции над матрицами (сложение, умножение матрицы на число, умножение матриц, возведение в степень, транспонирование).
Определители квадратных матриц (первого, второго и третьего порядка).
Свойства определителей.
Обратная матрица. Алгоритм вычисления обратной матрицы.
Ранг матрицы.
Системы линейных уравнений.
Решение системы линейных уравнений методом обратной матрицы.
Решение системы линейных уравнений с помощью формул Крамера.
Решение системы линейных уравнений методом Гаусса.
Векторы на плоскости и в пространстве. Свойства операций над векторами.
Размерность и базис векторного пространства.
Линейные операторы.
Собственные векторы и собственные значения линейного оператора.
Квадратичные формы.
Прямая на плоскости (уравнение прямой с угловым коэффициентом; уравнение пучка прямых, проходящих через точку; уравнение прямой, проходящей через две данные точки; уравнение прямой в отрезках, общее уравнение прямой).
Условия параллельности и перпендикулярности прямых. Угол между двумя прямыми.
Точка пересечения прямых. Расстояние от точки до прямой.
Окружность.
Эллипс.
Гипербола.
Парабола.
Контрольная работа по математике Вариант 1
1. Найти пределы следующих функций:
a).
;
b).
;
c).
;
d).
.
2. Исследовать функцию на непрерывность
(в точке
),
установить род точки разрыва:
.
3. Найти производные функций:
a).
;
b).
;
c).
;
d).
.
4. Исследовать функцию и построить ее график:
.
5. Найти полный дифференциал функции:
6. Найти интегралы:
a).
;
b).
;
c).
;
d).
.
7. Вычислить:
a).
;
b).
;
c).
;
d).
.
8. Решить систему линейных уравнений тремя способами:
a). методом обратной матрицы;
b). по формулам Крамера;
c). методом Гаусса
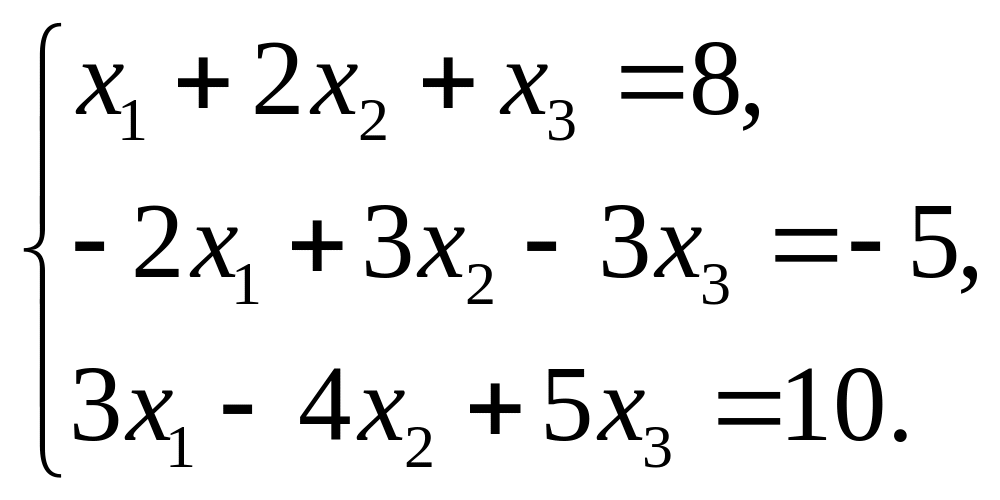
Вариант 1
9. Найти ранг матрицы:
.
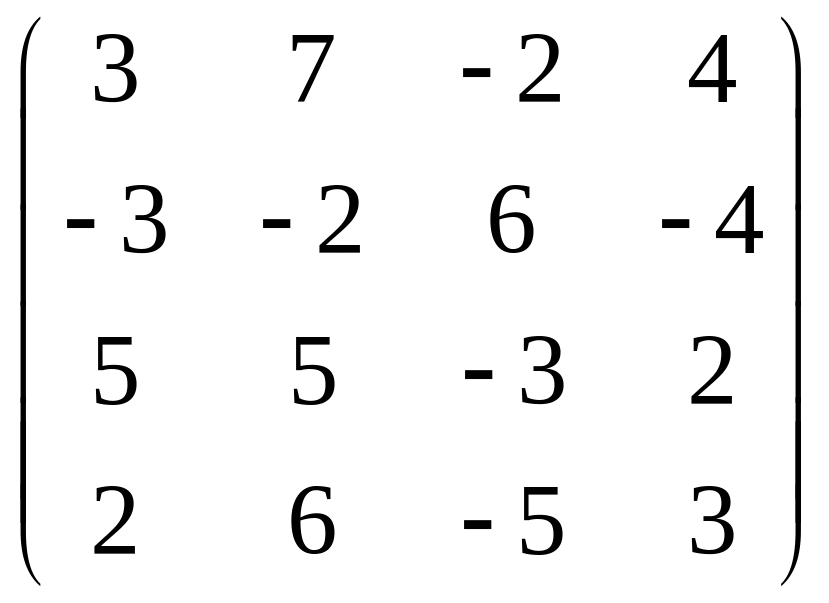10. Даны векторы
и
Найти угол между векторами
и
,
если
11. Найти собственные значения и
собственные векторы линейного оператора,
заданного матрицей:
12. Составить уравнение прямой, проходящей через точку A(2;3):
a). параллельно оси
OX; б). параллельно оси OY;
в). составляющей с осью OX угол
.
13. Составить уравнение прямой, проходящей
через центры окружностей
и
Найти отношение радиусов окружностей.