3.4Отчет о работе
Отчет должен содержать таблицу с исходными данными, промежуточными расчетами и полученными результатами.
Образец отчета показан на Рис. 3 -4.
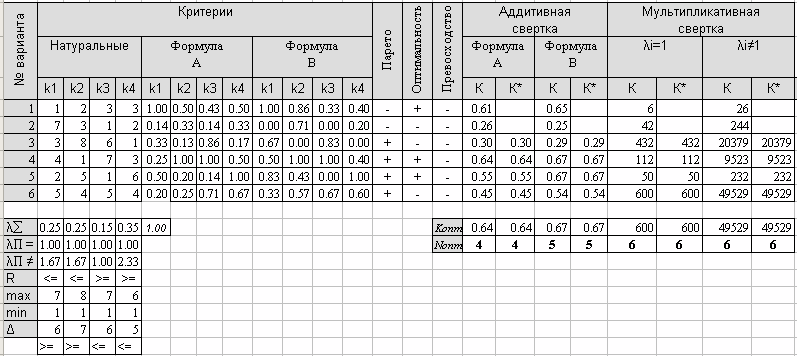
Рис. 3‑4. Пример отчета
Левая нижняя часть excel-листа содержит исходные и данные и ячейки для вспомогательных значений, используемых в выражениях для подсчета нужных значений.
В правой нижней части excel-листа приводятся полученные результаты – вычисленные значения скалярного критерия и номера наилучшей системы.
3.5Контрольные вопросы
Что называется частным показателем качества системы?
Что такое обобщенный показатель качества системы?
На какие основные классы распадаются критериев оценки сложных систем?
Какие элементы образуют множество Парето?
Как определяется аддитивный критерий свертки?
Из каких основных этапов состоит процедура свертки?
Как определяется мультипликативный критерий свертки?
В чем заключаются преимущества и недостатки аддитивного и мультипликативного критериев свертки?
3.6Варианты
1 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
2 |
4 |
2 |
2 |
6 |
4 |
1 |
1 |
3 |
5 |
2 |
5 |
1 |
4 |
4 |
1 |
5 |
3 |
5 |
3 |
7 |
5 |
4 |
6 |
2 |
1 |
7 |
3 |
i |
0.25 |
0.20 |
0.20 |
0.35 |
Kопт |
max |
max |
min |
max |
2 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
3 |
4 |
3 |
2 |
5 |
3 |
1 |
2 |
3 |
3 |
3 |
6 |
1 |
4 |
4 |
1 |
7 |
3 |
5 |
2 |
8 |
5 |
1 |
6 |
3 |
2 |
5 |
3 |
i |
0.15 |
0.40 |
0.20 |
0.25 |
Kопт |
max |
max |
min |
max |
3 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
2 |
4 |
3 |
2 |
8 |
3 |
1 |
2 |
3 |
3 |
3 |
6 |
1 |
4 |
4 |
1 |
7 |
3 |
5 |
2 |
4 |
2 |
1 |
6 |
3 |
2 |
5 |
3 |
i |
0.30 |
0.30 |
0.15 |
0.25 |
Kопт |
min |
min |
min |
max |
4 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
2 |
5 |
2 |
2 |
6 |
3 |
1 |
2 |
3 |
3 |
7 |
6 |
1 |
4 |
4 |
1 |
7 |
3 |
5 |
2 |
4 |
5 |
1 |
6 |
3 |
2 |
5 |
3 |
i |
0.10 |
0.40 |
0.10 |
0.35 |
Kопт |
min |
max |
min |
max |
5 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
2 |
4 |
2 |
2 |
7 |
4 |
1 |
3 |
3 |
5 |
2 |
6 |
1 |
4 |
6 |
1 |
5 |
3 |
5 |
2 |
4 |
5 |
4 |
6 |
2 |
1 |
8 |
3 |
i |
0.35 |
0.20 |
0.10 |
0.35 |
Kопт |
min |
min |
min |
max |
6 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
3 |
4 |
3 |
2 |
5 |
3 |
1 |
2 |
3 |
3 |
3 |
6 |
1 |
4 |
4 |
1 |
7 |
3 |
5 |
2 |
8 |
5 |
1 |
6 |
3 |
2 |
5 |
3 |
i |
0.15 |
0.40 |
0.20 |
0.25 |
Kопт |
max |
max |
min |
max |
7 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
2 |
4 |
3 |
2 |
8 |
3 |
1 |
2 |
3 |
3 |
3 |
6 |
1 |
4 |
4 |
1 |
7 |
2 |
5 |
2 |
4 |
2 |
1 |
6 |
3 |
2 |
5 |
3 |
i |
0.20 |
0.40 |
0.15 |
0.25 |
Kопт |
min |
max |
min |
min |
8 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
2 |
4 |
3 |
2 |
8 |
3 |
1 |
2 |
3 |
3 |
3 |
6 |
1 |
4 |
4 |
1 |
9 |
3 |
5 |
2 |
7 |
2 |
1 |
6 |
3 |
4 |
1 |
3 |
i |
0.30 |
0.30 |
0.15 |
0.25 |
Kопт |
min |
min |
min |
max |
9 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
5 |
3 |
3 |
2 |
8 |
4 |
2 |
3 |
3 |
5 |
2 |
6 |
1 |
4 |
6 |
1 |
5 |
3 |
5 |
2 |
4 |
5 |
2 |
6 |
2 |
1 |
8 |
3 |
i |
0.20 |
0.40 |
0.15 |
0.25 |
Kопт |
min |
max |
min |
min |
10 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
3 |
4 |
3 |
2 |
4 |
3 |
1 |
2 |
3 |
3 |
3 |
6 |
1 |
4 |
4 |
4 |
7 |
3 |
5 |
2 |
3 |
5 |
8 |
6 |
1 |
2 |
5 |
3 |
i |
0.50 |
0.20 |
0.15 |
0.15 |
Kопт |
min |
max |
max |
min |
11 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
2 |
4 |
3 |
2 |
5 |
3 |
1 |
2 |
3 |
3 |
4 |
6 |
1 |
4 |
4 |
1 |
7 |
2 |
5 |
2 |
6 |
2 |
1 |
6 |
3 |
2 |
5 |
3 |
i |
0.20 |
0.40 |
0.15 |
0.25 |
Kопт |
max |
max |
min |
min |
12 |
k1 |
k2 |
k3 |
k4 |
1 |
1 |
2 |
4 |
3 |
2 |
7 |
3 |
1 |
2 |
3 |
3 |
3 |
6 |
1 |
4 |
4 |
1 |
9 |
3 |
5 |
2 |
7 |
2 |
1 |
6 |
3 |
4 |
1 |
3 |
i |
0.30 |
0.30 |
0.15 |
0.25 |
Kопт |
min |
min |
max |
max |
13 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
2 |
5 |
2 |
2 |
5 |
3 |
1 |
2 |
3 |
3 |
7 |
6 |
1 |
4 |
4 |
2 |
7 |
3 |
5 |
2 |
4 |
5 |
1 |
6 |
3 |
2 |
5 |
3 |
i |
0.10 |
0.40 |
0.15 |
0.35 |
Kопт |
max |
min |
min |
max |
14 |
k1 |
k2 |
k3 |
k4 |
1 |
5 |
2 |
4 |
2 |
2 |
7 |
1 |
1 |
6 |
3 |
5 |
2 |
6 |
1 |
4 |
6 |
8 |
5 |
3 |
5 |
2 |
4 |
6 |
4 |
6 |
2 |
7 |
8 |
3 |
i |
0.35 |
0.20 |
0.10 |
0.35 |
Kопт |
min |
min |
min |
max |
15 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
2 |
4 |
3 |
2 |
7 |
3 |
1 |
2 |
3 |
3 |
3 |
6 |
1 |
4 |
4 |
2 |
7 |
3 |
5 |
3 |
4 |
2 |
1 |
6 |
4 |
2 |
5 |
3 |
i |
0.30 |
0.30 |
0.15 |
0.25 |
Kопт |
min |
max |
min |
max |
16 |
k1 |
k2 |
k3 |
k4 |
1 |
4 |
3 |
4 |
3 |
2 |
6 |
3 |
1 |
4 |
3 |
3 |
3 |
6 |
1 |
4 |
4 |
2 |
8 |
3 |
5 |
3 |
4 |
2 |
1 |
6 |
5 |
2 |
4 |
3 |
i |
0.25 |
0.20 |
0.25 |
0.30 |
Kопт |
max |
min |
min |
min |
17 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
3 |
4 |
3 |
2 |
2 |
3 |
1 |
4 |
3 |
1 |
3 |
6 |
3 |
4 |
3 |
4 |
7 |
4 |
5 |
8 |
3 |
5 |
2 |
6 |
3 |
2 |
5 |
1 |
i |
0.50 |
0.20 |
0.15 |
0.15 |
Kопт |
min |
min |
max |
min |
18 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
2 |
4 |
3 |
2 |
3 |
4 |
1 |
2 |
3 |
3 |
1 |
6 |
1 |
4 |
4 |
1 |
3 |
2 |
5 |
2 |
6 |
2 |
1 |
6 |
3 |
2 |
5 |
3 |
i |
0.20 |
0.40 |
0.15 |
0.25 |
Kопт |
max |
max |
min |
min |
19 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
2 |
4 |
3 |
2 |
6 |
3 |
1 |
2 |
3 |
3 |
3 |
6 |
1 |
4 |
4 |
1 |
8 |
3 |
5 |
2 |
7 |
2 |
1 |
6 |
3 |
4 |
1 |
3 |
i |
0.35 |
0.30 |
0.15 |
0.20 |
Kопт |
min |
min |
min |
max |
20 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
5 |
3 |
3 |
2 |
8 |
4 |
2 |
3 |
3 |
5 |
2 |
6 |
1 |
4 |
6 |
1 |
5 |
3 |
5 |
2 |
4 |
5 |
2 |
6 |
2 |
1 |
8 |
3 |
i |
0.25 |
0.35 |
0.20 |
0.20 |
Kопт |
min |
max |
min |
min |
21 |
k1 |
k2 |
k3 |
k4 |
1 |
1 |
2 |
4 |
3 |
2 |
7 |
3 |
1 |
2 |
3 |
3 |
3 |
6 |
1 |
4 |
4 |
1 |
9 |
3 |
5 |
2 |
7 |
2 |
1 |
6 |
3 |
4 |
5 |
3 |
i |
0.25 |
0.25 |
0.15 |
0.35 |
Kопт |
min |
min |
max |
max |
22 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
4 |
5 |
2 |
2 |
5 |
3 |
1 |
2 |
3 |
3 |
7 |
6 |
1 |
4 |
4 |
2 |
7 |
3 |
5 |
2 |
4 |
5 |
1 |
6 |
3 |
2 |
5 |
3 |
i |
0.15 |
0.35 |
0.15 |
0.35 |
Kопт |
min |
max |
min |
max |
23 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
2 |
4 |
3 |
2 |
8 |
3 |
1 |
2 |
3 |
3 |
3 |
6 |
4 |
4 |
4 |
5 |
7 |
3 |
5 |
3 |
4 |
2 |
1 |
6 |
4 |
2 |
5 |
3 |
i |
0.10 |
0.35 |
0.20 |
0.35 |
Kопт |
max |
max |
min |
max |
24 |
k1 |
k2 |
k3 |
k4 |
1 |
3 |
2 |
4 |
3 |
2 |
4 |
4 |
1 |
2 |
3 |
3 |
1 |
6 |
1 |
4 |
5 |
1 |
3 |
2 |
5 |
2 |
6 |
2 |
1 |
6 |
3 |
2 |
5 |
3 |
i |
0.30 |
0.30 |
0.15 |
0.25 |
Kопт |
max |
max |
min |
min |
4Сетевое планирование и управление
4.1Цель работы
Изучение детерминированной и вероятностной сетевой модели планирования и управления.
4.2Теоретические сведения
4.2.1Основные понятия
Сетевое планирование и управление [5] – метод исследования и проектирования сложных систем. Метод позволяет провести анализ и оптимизацию процессов, состоящих из связанных подсистем или совокупности последовательных и взаимосвязанных работ и событий. Основой для анализа и расчетов процессов является математическая модель в виде ориентированного графа [Рис. 4 -5], называемая сетевой моделью.
Рис. 4‑5 Пример простейшей сетевой модели
Основными элементами сетевой модели являются событие, работа и путь.
Работа - процесс, связанный с затратами времени и ресурсов, и приводящий к достижению определенных результатов. (Работами следует считать также процессы, не требующие расходов ресурса, но только времени).
Ресурсы - материалы, сырье, оборудование, контингент исполнителей, необходимые для производства работы, финансовые средства и прочее.
Фиктивная работа отображает логическую связь работ и не требует расхода времени и ресурсов (работа (1,3) на Рис. 4 -5). Она только констатирует, что событие (3) не может произойти, пока не свершится событие (1).
В сетевых моделях работы отображаются направленными стрелками, фиктивная работа – пунктиром, рядом с ними изображаются длительности работ t(i,j).
Событие - факт завершения всех предшествующих работ и готовности к выполнению всех последующих.
Каждая работа в сети характеризуется:
начальным событием – (i);
конечным событием – (j);
Работы кодируются в терминах событий, т.е. каждая из них идентифицируется своими начальным и конечным событиями. Работы с одинаковыми i j не допускаются. В этом случае следует ввести фиктивные работы, которые обеспечивают необходимую развязку.
Исходное событие («самое начальное») сети (0) иногда обозначается (I); завершающее событие («самое конечное») – (С).