
- •1. Общие сведения о подобии и моделировании
- •2. Основные понятия и определения
- •3. Теоремы подобия
- •4. Нахождение критериев подобия на основе анализа уравнений
- •5. Получение критериев подобия, когда уравнение процесса
- •6.Некоторые критерии теплофизических процессов
- •7. Задачи моделирования процессов
5. Получение критериев подобия, когда уравнение процесса
не известно.
5.1. Единицы измерений и анализ размерностей
Критерии подобия в этом случае, когда уравнение процесса неизвестно можно получить на основе анализа размерностей.
В настоящее время применяется Международная система единиц измерения "СИ", в которой выбраны следующие, независимые друг от друга величины измерения: массы – кг (килограмм); длины – м (метр), времени – с(секунда); температуры – K (градусы Кельвина); силы тока – А (ампер);
количества вещества – n (моль) и силы света – Y (кандела). Эти величины
называются первичными единицами измерения. Через них выражаются все
остальные единицы измерения, которые называются вторичными, или производными.
Формула, указывающая зависимость единицы измерения производной
величины от основных единиц измерения, называется размерностью этой величины. Например, определительным уравнением для скорости является уравнение V = dl / dt.
Принято использовать следующие символы для выражения размерностей величин: М – масса, L – длина, Т – время, θ – градусы температуры, I – сила тока, n – количество вещества Y – сила света.
Символы обычно помещаются в квадратные скобки. Например, для
скорости размерность будет выглядеть так: [V] = [L] [T]-1.
Поскольку определительное уравнение для силы согласно второму закону Ньютона есть F = m a, то [F] = [M] [L] [T]-2. Для работы определительное уравнение A = Fl, то [A] = [M] [L]2 [T]-2.
Необходимо иметь в виду, что размерность любой физической величины представляет собой произведение возведенных в какие – либо степени размерностей первичных величин.
Хотя число первичных величин в общем случае равно семи, обычно не все они одновременно используются при решении конкретных задач, причем тип используемых величин зависит от области знаний или техники, к которой относится данная задача. Так, для механической системы достаточно трех, а для теплофизической четырёх первичных величин: длины, массы, времени, температуры.
В механической системе размерность любой физической величины Q может быть выражена через размерности трех первичных величин следующим образом: [Q] = [M]α [L]β [T]λ, где пока неизвестные показатели степени α, β, λ подлежат определению.
5.2. Процедура нахождение критериев подобия
Для определения критериев с помощью этого способа необходимо:
− выявить n параметров Р1, Р2, ..., Рn, которые характеризуют изучаемый процесс;
− составить матрицы размерностей n параметров;
− установить числа r независимых между собой параметров;
− представить описания изучаемого явления в критериальной форме;
− составить n−r выражений критериев подобия.
5.3. Примеры нахождения критериев на основе анализа размерностей
5.3.1. Найти критерии подобия процесса движения тела заданной формы в жидкости.
В соответствии с условием задачи выделим шесть величин (n = 6), характеризующих заданный процесс:
P1 = ; P2 =g; P3 = F; P4 = l; P5 = ν; P6 = ρ,
где – скорость тела, м/с; g – ускорение тяготения, м/с2; F – сила сопротивления движению тела, Н; l – характерный размер тела, м;
ν – кинематическая вязкость жидкости, м2/с; ρ – плотность жидкости, кг/м3.
Таким образом, функциональная зависимость, подлежащая исследованию, имеет вид
φ
= (
,
g,
F,
 ,
ν,
ρ).
,
ν,
ρ).
Выберем три (r = 3) независимых величины и пусть это будут l, и ρ, размерности которых составят систему уравнений:
 ;
;
 ;
(1)
;
(1)
 .
.
Для остальных трёх величин уравнения размерностей будут иметь вид:
 .
.
 (2)
(2)

Проверим правильность сделанного выбора числа независимых параметров (r = 3), составив матрицу размерностей уравнений (1):

Как
видно определитель матрицы
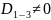 и следовательно выбранные величины
l,
,
ρ
действительно независимы.
и следовательно выбранные величины
l,
,
ρ
действительно независимы.
Нахождение критериев подобия заключается в определении формы записи их и далее в отыскании значений показателей степени μs.., λs .., τs.
Применительно к данному примеру для оставшихся трёх величин уравнений (2) получим соотношения в виде безразмерных комплексов:
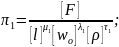


Найти показатели степени можно, выразив все величины, входящие в безразмерные комплексы, через основные единицы измерений.
К
примеру, в комплексе
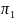 раскрыв размерности силы, скорости и
плотности, как
,
раскрыв размерности силы, скорости и
плотности, как
,
 и
и
 запишем
запишем

Отсюда, приравняв показатели одноименных основных величин, стоящих в числителе и знаменателе, получим:
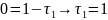 при
при
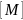 ;
;
0
=
 при
при

0
= при
при

Выполнив аналогичные процедуры с остальными двумя безразмерными комплексами, получим в конечном итоге критерии подобия процесса в виде:

 ;
;
 .
.
Полученные
критерии можно преобразовать и сделать
эквивалентными по записи найденным
ранее при анализе уравнения движения
жидкости. Так обратные величины комплексов
 и
и
 являются соответственно критериями
Рейнольдса
и Фруда
являются соответственно критериями
Рейнольдса
и Фруда

Как видим, нахождения критериев подобия из анализа уравнения процесса и анализа размерностей параметров этого же процесса приводит к одинаковым результатам.
5.3.2.
Методом анализа размерностей найти
критерии, которые обеспечат подобие
процессу нестационарной теплопроводности
при наличии в теле постоянно действующего
источника тепла мощностью qv.
Уравнение этого процесса
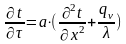 .
.
Итак, в состав этого равенства входят шесть параметров (n=6) и соответственно температура тела есть неявной функцией следующих параметров:
 .
.
Запишем функцию t в явном виде, допуская, что между функцией и параметрами существует степенная зависимость:
 (1)
(1)
где b- безразмерный коэффициент пропорциональности.
Для записанного равенства размерности левой и правой частей должны быть одинаковыми, итак:
 (2)
(2)
Сведём
размерности производных величин  ,
,
q
v
к основным: метр (м), секунда (с), температура
(t)
и масса (кг). Получим:
,
,
q
v
к основным: метр (м), секунда (с), температура
(t)
и масса (кг). Получим:
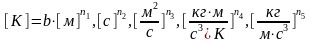 (3)
(3)
Показатели степени при одинаковых основных единицах в обеих частях уравнения (3) должны быть одинаковыми. Итак, получим систему равенств:



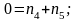
Имеем
пять неизвестных
 и четыре равенства. Решив совместно
систему этих равенств относительно n
2 ,
получим:
и четыре равенства. Решив совместно
систему этих равенств относительно n
2 ,
получим:




С учётом показателей степени равенство (1) примет вид:

Последнее равенство запишем в безразмерной форме делением левой и правой его частей на t:
 .
.
Объединив величины с одинаковыми степенями в безразмерные комплексы, получим:

 .
.
Имеем два безразмерных комплекса (критерия), которые определяют условие подобия данного процесса.
Если вместо
подставить его
значение
 ,
то получим:
,
то получим:
 .
.
Итак, с помощью метода анализа размерностей получили критерии подобия аналогичные тем, что были получены раннее по уравнению процесса (задача 4.2.2).
