Механизмы стимулирования в задачах формирования состава организационной системой - Губко М.В

Механизмы стимулирования в задачах формирования состава

организационной системы

Губко М.В.

(Институт Проблем Управления РАН, Москва)

Резюме

Вданной работе на примере простой модели стимулирования

вактивной системе рассмотрены и решены задачи первоначально- го формирования состава активных элементов (АЭ) и задача привлечения дополнительных АЭ.

Введение

Задачи формирования состава пока слабо изучены в рамках Теории активных систем (ТАС). Эти задачи являются предметом изучения других областей науки управления (теории операций и пр.), однако пока имеется весьма малое количество работ, учиты-

вающих активность поведения участников в задачах формирования состава [КУП, МС Много. АС]. Целью данной работы является рассмотрение задач формирования состава с точки зрения ТАС,

для чего вводится система классификации задач формирования состава для задачи стимулирования и, на примере простой модели, показывается, каким образом результаты ТАС могут быть приме- нены для их решения.

1. Описание модели и обозначения

Рассмотрим задачу стимулирования в системе с n АЭ. Обозна- чим через N множество АЭ.

1

Пусть Ф( y) = H ( y) - åσ i ( yi ) – целевая функция центра.

i N

При этом действие каждого АЭ yi Î Ai , y := ( y1,..., yn ) – вектор

(профиль) действий АЭ, H(y) – доход центра от данного профиля, вогнутая по каждой компоненте yi функция.

fi ( yi ) = σ i ( yi ) - ci ( yi ) – целевая функция АЭ, при этом за- траты ci ( yi ) – выпуклая функция, зависящая только от действия i-го АЭ.

Можно рассматривать также сепарабельные затраты вида ci ( y) = ci1( yi ) + ci2 ( y−i ) . Эта задача будет эквивалентна исходной с

Определим доход центра в задаче стимулирования с данным фиксированным составом исполнителей N.

Далее в тексте вводится упрощающее предположение, что

(1) H ( y) = H (åyi ) ,

i N

то есть доход центра зависит только от общего объема производст- ва (это случай, например, когда все АЭ производят одинаковую

2

продукцию). Тогда условие на y* можно записать в виде системы уравнений c'1 ( yi* ) = ... = c'n ( yi* ) = H '( y* ) . То есть в точке

равновесия производные затрат АЭ равны между собой.

Целевая функция центра в равновесии запишется как

(2) Фmax ( y* ) = H (åyi* ) - åci ( yi* ) .

i N i N

Введем дополнительные обозначения Y = å yi (реализуемый

2.Задачи формирования состава

Врамках данной модели рассматриваются следующие задачи формирования состава:

I.Для имеющегося множества N принять решение о вклю- чении или невключении в систему нового исполнителя a (a - additional) с функцией затрат ca ( ya ) = ca0 + ea ( ya )

1.не меняя функций стимулирования прочих АЭ;

2.изменяя функции стимулирования прочих АЭ.

а) без изменения имеющегося состава N

3

б) с возможностью замены новым АЭ одного из имеющихся.

II.Для заданного множества претендентов N0 определить оптимальный состав исполнителей N.

III.Для имеющегося множества N и заданного множества

претендентов N0 определить новый оптимальный состав исполнителей N’.

1.не меняя функций стимулирования имеющихся АЭ;

2.изменяя функции стимулирования имеющихся АЭ.

а) без изменения имеющегося состава N

б) с возможностью замены новыми АЭ одного или нескольких из уже имеющихся.

Задачи I, III относится к случаю уже функционирующей сис- темы, а задача II – к случаю начального определения состава сис- темы.

Задача III и ее модификации представляет собой общий случай задачи формирования состава. Действительно, полагая в ней N = получаем задачу первоначального формирования состава II. Полагая N0={a}, получаем задачу I. При N = задача становится «задачей об увольнениях» - задачей оптимизации имеющегося состава исполнителей.

Задача I.1

Сучетом пришедшего игрока

(4)Фd ( ya ) = H (Y * + ya ) − C0 − ca0 − E(Y * ) − ea ( ya ) (d обозначает distorted).

Принимать на работу нового сотрудника имеет смысл, если от этого увеличивается целевая функция центра, то есть

(5) maxФd ( ya ) > Фmax = Ф(Y * ) .

ya ³0

Условие выгодности привлечения нового АЭ принимает вид:

4

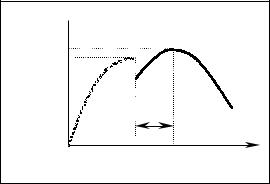
Или, иначе,

(6) max[DH ( ya ) - ca ( ya )] > 0 .

ya ³0

В отличие от предыдущей модели, при введении нового АЭ мы пересчитываем планы и стимулирование всех элементов системы.

Тогда целевая функция центра в обоих случаях будет выглядеть так:

Доказательство: надо доказать, что

5

Преобразуя минимум в левой части к двум последовательным минимумам, получаем утверждение леммы. •

Лемма 1 позволяет свести задачу к задаче стимулирования для двух игроков: нового АЭ a, и игрока (затраты которого описыва- ются функцией C(Y)), представляющего старую систему.

Тем не менее, задачу можно еще упростить, если число игро- ков n велико и функции H(Y) и C(Y) можно линеаризовать в окрестности точки Y*. Тогда, так как Y* – точка равновесия, то

H '(Y * ) = -C'(Y * ) , поэтому линеаризация выглядит следующим образом:

(9) H (Y ) = H (Y * ) + α(Y - Y * ) , C(Y ) = C(Y * ) -α(Y -Y * ) , где

α – маржинальные затраты (или, что то же самое – маржинальный доход в «старой» точке равновесия). Тогда

6

Можно вычислить внутренний минимум выражения (10). Ус- ловие Лагранжа (равновесные значения Y и ya обозначены знаком **, в отличие от «старого» равновесия Y*) дает условие на произ-

водную затрат нового АЭ: α = c'a ( ya** ) . Отсюда можно выразить ya** = [c'a ]−1(α) . Тогда Y ** = Y '- ya** и условие (10) преобразуется

к выражению

(11) max[αY '-α(Y '- ya** ) - ca ( ya** )}] = α × ya** - ca ( ya** ) > 0 .

Y '

Сведение к линейному случаю привело к исчезновению Y’ из максиимзируемого выражения. Значит, в линейном случае, выбор Y’ (из малой окрестности точки Y*) не влияет на результат центра.

Если выбрать Y ** = Y * , то результат решения линеаризованной задачи I.2 совпадает с решением линеаризованной задачи I.1 (получаемой из условия (6) подстановкой выражений (9)). Поэтому линейного случая недостаточно, чтобы исследовать разницу между результатами I.1 и I.2. Изменение планов «старых» игроков в задаче I.2 дает прибавку второго порядка к результату центра.

Вто же время, добавление все новых и новых участников все больше сдвигает профиль планов «старых» участников от опти- мального (рассчитанного для исходного состава N). То есть изредка все же надо пересчитывать планы на новый состав, даже

если изменение уже существующих планов приводит к проблемам организационного плана.

Вто же время, пересчет оптимальных планов при введении

нового АЭ сводится к вычислению новой функции совокупных

затрат CN +a (YN +a ) = min [CN (YN ) + ca ( ya )] и последующей

YN + ya =YN +a

оптимизации ФN+a(.), что, в общем-то, несложно (если и CN, и ca известны).

Полезно для текущего состава рассчитывать оптимальные планы yi*(Y ) в некоторой окрестности плана Y*, на случай

7

изменения функции дохода центра H(.) или добавления новых сотрудников.

Задача II

«Прямолинейный» подход к задаче первоначального форми- рования состава N участников из множества претендентов N0 (каждый из претендентов полностью описывается своей функцией

затрат ci(yi)), состоит в рассмотрении 2N 0 -1 задач стимулирова-

ния для каждого непустого подмножества N0 и последующего выбора подмножесва, доставляющего максимум целевой функции центра. Никаких теоретических сложностей эта процедура не вызывает, однако вычислительно она довольно трудоемка.

Решение задачи стимулирования (с учетом упрощения (1)) для каждого N Í N0 состоит из следующих этапов:

1.Вычисление совокупной функции затрат

(12) CN (Y ) = min åci ( yi ) (задача выпуклой оптимизации с N

y: å yi =Y i N i N

переменными и одним ограничением).

2.Вычисление

Сокращение количества рассматриваемых составов

Один из возможных подходов состоит в выработке условий для сокращения множества рассматриваемых составов. Примеры таких условий рассмотрены ниже.

8

(множество таких игроков обозначим M) этот факт позволяет

сократить возможное число рассматриваемых составов только составами, в которые входят игроки M.

Рассмотрим АЭ с линейными затратами, то есть с затратами

вида ci ( yi ) = ci0 + γ i yi .

Выражение (12) для произвольного состава N запишется в

«дешевый» АЭ, остальные получают нулевой план и минимальную ставку ci0 . Поэтому очевидно, что в линейном случае кандидатами на оптимальный состав могут быть системы с одним АЭ.

Решая, таким образом, N0 задач стимулирования (для системы с одним участником), определяем для каждой такой системы доход центра и выбираем работника, максимизирующего этот доход. Результирующее выражение выглядит следующим образом:

Таким образом, даже рассмотрение линейных функций затрат, хоть и упрощает задачу, все же не позволяет ввести ранжирование АЭ на основании только их функции затрат, что позволило бы, не решая задачу стимулирования, принять решение об оптимальном составе исполнителей.

Сведение к задаче оптимизации разрывной функции

Другой возможный подход состоит в модификации самой за- дачи следующим образом:

9

Определим функции затрат претендентов следующим образом:

Если оптимальный план некоторого АЭ равен нулю, значит, этот АЭ не входит в оптимальный состав исполнителей. Этот прием

позволяет свести 2( 2N 0 -1 ) задач оптимизации к двум, но с разрывными функциями.

Пример: Рассмотрим задачу первоначального формирования состава исполнителей в случае двух кандидатов:

c1( y1) = 2 + y12 , c2 ( y2 ) = 1+ 2y22 .

При этом первый кандидат отличается относительно большей производительностью (его функция затрат возрастает более полого), но и более высокими начальными затратами, чем второй.

Пусть доход центра возрастает линейно, H (Y ) = αY .

В случае двух элементов нужно рассмотреть лишь три возможных состава и непосредственно построить функции затрат для каждого

функции затрат системы, состоящей из первого АЭ, второго АЭ и обоих АЭ соответственно.

Очевидно, что C~(Y ) = min[C1(Y ),C2 (Y ),C12 (Y )].

10