9.2. Внутренние степени свободы молекул

Число степеней свободы − это число независимых координат (переменных), которые полностью определяют положение системы в пространстве.

М олекулу одноатомного газа рассматривают как материальную точку, которой приписывают три степени свободы поступательного движения. Молекула двухатомного газа рассматривается как совокупность двух материальных точек, жестко связанных недеформированной связью. Эта система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Вращение вокруг третьей оси, которая проходит через оба атома, не меняет положение молекулы в пространстве (рис. 9.2.1, а). Трехатомная молекула имеет шесть степеней свободы: три поступательные и три вращательные (рис. 9.2.1, б). Столько же степеней свободы будут иметь и многоатомные молекулы (четырех, пяти и т. д.).

9.3. Закон распределения энергии молекулы по степеням свободы

Так как на поступательное движение приходится три степени свободы, то согласно выражению (9.1.21) на одну поступательную степень свободы в среднем приходится энергия

. (9.3.1)

Возникает вопрос, какая энергия в среднем приходится на вращательную степень свободы. В классической статистической физике выводится закон (теорема) Больцмана о равномерном распределении энергии по степеням свободы: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная .

Таким образом, кинетическая энергия одной молекулы, с жестко связанными атомами равна

, (9.3.2)

где i − число степеней свободы.

Естественно, что жесткой связи между атомами не существует, поэтому для реальных молекул необходимо учитывать также степени свободы колебательного движения. Колебательная степень обладает вдвое большей энергией потому, что на нее приходится не только кинетическая, но и потенциальная энергия. Причем средние значения кинетической и потенциальной энергий одинаковы. Поэтому на каждую колебательную степень свободы − в среднем приходится энергия равная kT.

В этом случае полное число степеней свободы для молекулы газа равно

i = i_п + i_вр + 2i_k , (9.3.3)

где i_п – число поступательных степеней свободы; i_вр – число вращательных степеней свободы; 2i_k ‑ число колебательных степеней свободы.

9.4. Внутренняя энергия идеального газа

В середине XIX в. было доказано, что наряду с механической энергией макроскопические тела обладают еще и энергией, заключенной внутри самих тел. С точки зрения молекулярно-кинетической теории внутренняя энергия макроскопического тела равна сумме кинетических энергий теплового движения всех молекул и потенциальных энергий взаимодействия всех молекул друг с другом.

Внутренняя энергия идеального газа равна сумме кинетических энергий теплового движения всех молекул газа, т. к. потенциальная энергия взаимодействия равна нулю (отсутствуют силы взаимодействие).

Внутренняя энергия идеального газа равна

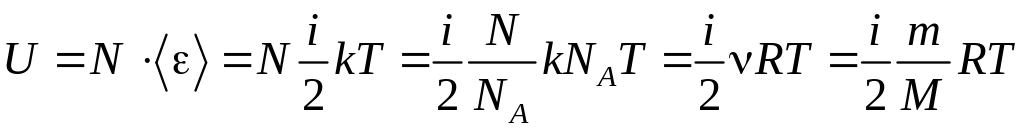. (9.4.1)

где kN_A = R − универсальная газовая постоянная.

Малое изменение внутренней энергии определяется соотношением

, (9.4.2)

конечное изменение внутренней энергии соотношением

. (9.4.3)