6.4. Скорость распространения волн в различных средах

Для определения скорости упругих волн в упругой среде рассмотрим продольную плоскую волну, распространяющуюся в направлении оси 0х. Выделим в среде цилиндрический объем с площадью основания S₀ и высотой dx. Смещения S частиц с разными х в каждый момент времени оказываются различными. Если основание цилиндра с координатой х имеет в некоторый момент времени смещение S, то смещение основания с координатой x + dx будет S + dS. Тогда, рассматриваемый объем деформируется и получает удлинение dS или относительную деформацию  = S/x (деформации растяжения). Наличие деформации свидетельствует о существовании нормального напряжения , которое при малых деформациях пропорционального величине деформации. По закону Гука для деформации растяжения − сжатия

, (6.4.1)

где Е − модуль Юнга среды.

Из зависимости смещения от координаты х видно, что относительная деформация S/x, а также, и напряжение  в фиксированный момент времени зависят от х. В соответствии с этим, продольная волна состоит из чередующихся разрежений и сжатий среды.

Теперь для цилиндрического объема запишем уравнение движения. Масса этого объема

. (6.4.2)

где  − плотность недеформированной среды.

Ввиду малости dx можно считать ускорение всех точек цилиндра одинаковым и равным

. (6.4.3)

Тогда этот участок объема будет растянут под влиянием сил F₁ и F₂ , приложенных к основаниям цилиндра в данный момент времени. Силы, действующие на левое и правое основание цилиндра равны, соответственно

. (6.4.4)

После разложения силы F₂ в ряд, получим

, (6.4.5)

и результирующая F₁ , F₂ сил, действующая на элемент объема равна

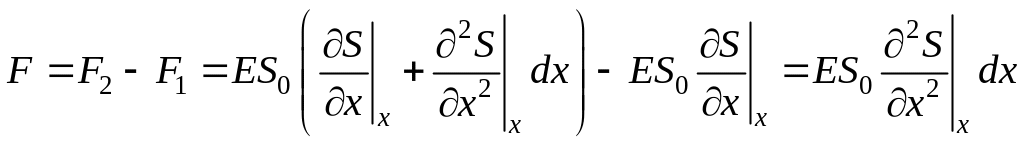. (6.4.6)

Используя основное уравнение динамики поступательного движения (2.1.2) и, подставив значения массы, ускорения и силы, получим

. (6.4.7)

Из сравнения этого уравнения с волновым уравнением для плоской волны (6.3.6) , получим

 , (6.4.8)

где Е − модуль Юнга.

Полученное уравнение определяет фазовую скорость продольных упругих волн.

Если проделать аналогичные преобразования для поперечных упругих волн, то фазовая скорость поперечных упругих волн будет иметь следующий вид

, (6.4.9)

где G − модуль сдвига.

6. Механические волны Лекция № 10

6.5. Волновой перенос энергии и его характеристики: поток, плотность потока, интенсивность.

6.6. Фазовая и групповая скорости волн.

6.7. Интерференция упругих волн.

6.8. Стоячие волны.

6.5. Волновой перенос энергии и его характеристики: поток, плотность потока, интенсивность

Пусть в некоторой среде распространяется в направлении оси 0х плоская продольная волна . Выделим в среде элементарный объем , настолько малый, чтобы скорость движения и деформацию во всех точках этого объема можно было считать одинаковыми и равными. Выделенный объем обладает кинетической энергией . Если масса , а , то

. (6.5.1)

Потенциальная энергия упругой деформации рассматриваемого объема

, (6.5.2)

где ; l₀ − первоначальная длина рассматриваемого объема; − относительная деформация объема; − первоначальный объем. Используя формулу (6.4.8) и, учитывая, что , получим

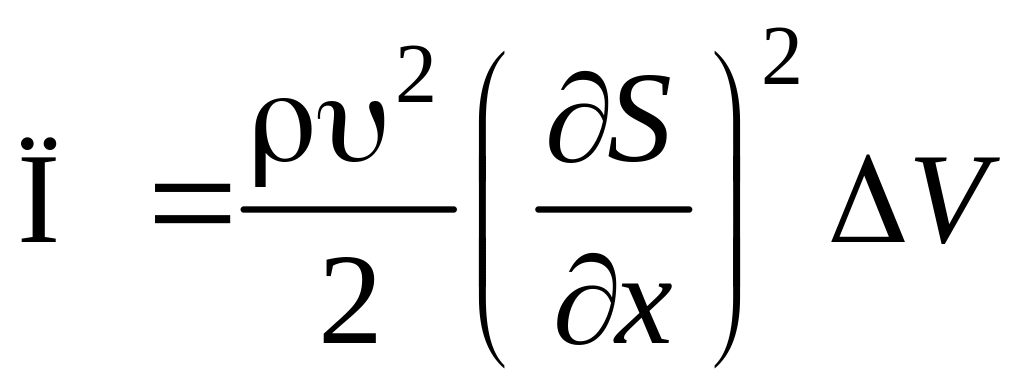. (6.5.3)

Тогда полная энергия упругой волны

. (6.5.4)

Определим плотность энергии, разделив (6.5.4) на объем

. (6.5.5)

Продифференцируем уравнение плоской продольной волны (6.2.8) по времени t и по координате х и подставим выражения в формулу (6.5.5) учтя, что

. (6.5.6)

Среднее значение квадрата синуса равно 1/2. Соответственно среднее по времени значение плотности энергии в каждой точке среды равно

. (6.5.7)

Таким образом, плотность энергии и среднее значение плотности энергии пропорциональны плотности среды , квадрату частоты  и квадрату амплитуды волны А.

Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии через эту поверхность. Поток энергии Ф через данную поверхность равен энергии dW переносимой за время dt

. (6.5.8)

Ф измеряется в ваттах.

Для характеристики распространения энергии в разных точках пространства вводится векторная величина, называема плотностью потока энергии. Плотность потока энергии численно равна потоку энергии через единичную площадку , помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.

Если через площадку , перпендикулярную к направлению распространения волны, переносится энергия за время , то плотность потока энергии равна

. (6.5.9)

Рассмотрим объем цилиндра с основанием и высотой ( − фазовая скорость волны). В случае малого объема цилиндра, плотность энергии во всех точках цилиндра можно было считать одинаковой и поэтому энергию можно найти как произведение плотности энергии  на объем

. (6.5.10)

Подставив выражение (6.5.10) в последнее выражение, получим

или , (6.5.11)

где − вектор плотности потока энергии, называемый вектором Умова.

Интенсивность волны равна

. (6.5.12)

Данное выражение справедливо для волны любого вида.

Определим поток энергии через поверхность S. Для этого разобьем поверхность на элементарные участки dS. За время dt через площадку dS пройдет энергия dW. Объем цилиндра, где вычисляется энергия, равен . Тогда в этом объеме содержится энергия

, (6.5.13)

где ; − единичный вектор нормали к поверхности dS.

Поток энергии через элементарную поверхность dS

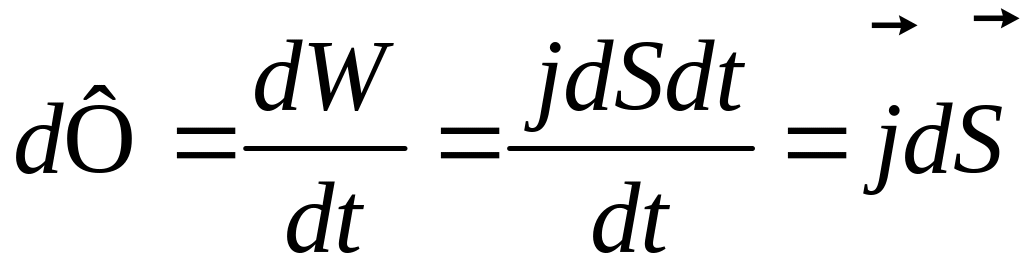. (6.5.14)

Поток энергии через поверхность S равен

. (6.5.15)