1 Расчётно-проектировочное задание №4. Расчёт вала при

совместном действии изгиба и кручения

Совместное действие изгиба и кручения относится к сложному сопротивлению. При таком виде нагружения под действием сил, передающихся на вал от шкивов или колес, в поперечных сечениях вала возникают крутящий и изгибающий моменты (рисунок 1.1).

а - шкив; б- колесо

Рисунок 1.1 – К определению внутренних силовых факторов

Если вал вращается с некоторой частотой, то угол поворота его за секунду (угловая скорость) рассчитывается по формуле

, (1.1)

где n – число оборотов вала в минуту.

Мощность, передаваемая валом, является работой внешнего момента, воспринимаемого валом:

. (1.2)

Для определения внешних нагрузок необходимо привести все нагрузки, действующие со стороны шкива или колеса, к центру тяжести вала диаметром d.

Через шкив (рисунок 1.1, а) перекинуты приводные ремни, имеющие натяжения n∙t и t. Тогда внешний момент, воспринимаемый валом со стороны шкива, равен:

. (1.3)

Изгибающее усилие, воспринимаемое валом со стороны шкива, определяем по формуле

. (1.4)

Внешний момент, воспринимаемый валом со стороны колеса (рисунок 1.1, б), рассчитывается по формуле

, (1.5)

где Р – окружное усилие на колесе, которое является силой давления на вал со стороны колеса.

Внешний момент вызывает кручение вала, а силы давления – его изгиб. Поэтому для определения опасного сечения необходимо построить эпюры изгибающих и крутящих моментов. Эпюра крутящего момента строится в соответствии со схемой действия внешних моментов.

Силы давления раскладывают на вертикальные и горизонтальные составляющие и строят эпюры изгибающих моментов в горизонтальной М_х и вертикальной М_у плоскостях соответственно. Требуется отметить, что каждое из сечений вала испытывает прямой поперечный изгиб от действия суммарного изгибающего момента, который определяется по формуле

. (1.6)

Так как сечения вала испытывают сложное напряженное состояние, то условие прочности по III и IV теориям прочности можно записать в следующем виде:

, (1.7)

где – эквивалентные моменты, вычисленные по III и IV теориям прочности по формулам соответственно:

; (1.8)

, (1.9)

W_x – осевой момент сопротивления круглого поперечного сечения вала диаметром d, который можно рассчитать по формуле

. (1.10)

1.1 Пример выполнения расчетно-проектировочного задания №4

Исходные данные: вал, расчетная схема которого приведена на рисунке 1.2, а, вращается с угловой скоростью ω=70 рад/c. Шкив диаметром D=0,6 м и углом наклона ветвей гибкой передачи α=20⁰ передает мощность N, равную 26 кВт. Собственный вес шкива G=0,5 кН. На валу установлены шестерни диаметрами D₁=0,3 м и D₂=0,2 м. Известно, что шестерня диаметром D₁ передает мощность N₁, равную 15 кВт. Направления окружных усилий шестерен показаны на рисунке 1.2.

Требуется: определить диаметр вала по третьей теории прочности, если допускаемое напряжение для заданного материала [σ]=80 МПа.

Решение

1 Определяем внешние крутящие моменты, передаваемые шкивом D и шестерней D₁, в соответствии с уравнением (1.2):

2 Составляем схему действия на вал внешних крутящих моментов (рисунок 1.2, б) и из условия равновесия вала определяем внешний момент на шестерне D₂:

3 Строим эпюру крутящих моментов (рисунок 1.2, в).

4 Определяем усилие натяжения ветвей ременной передачи и изгибающее усилие, передаваемое валу со стороны шкива (формулы (1.3) и (1.4)):

;

.

5 Находим соответствующие окружные усилия шестерен по формуле (1.5)

;

.

6 Приводим действующие нагрузки к центру тяжести вала (рисунок 1.2, г) и определяем вертикальные и горизонтальные составляющие усилий, действующие со стороны шкива и шестерен на вал:

7 Составляем схему действия на вал всех усилий в вертикальной плоскости (рисунок 1.2, д), находим значения опорных реакций и строим эпюру изгибающих моментов М_х (рисунок 1.2, е).

8 Составляем схему действия на вал всех усилий в горизонтальной плоскости (рисунок 1.2, ж), находим значения опорных реакций и строим эпюру изгибающих моментов М_у (рисунок 1.2, з).

9 Определяем величины суммарных изгибающих моментов в характерных сечениях вала при помощи зависимости (1.6), и строим эпюру суммарных изгибающих моментов (рисунок 1.2, и):

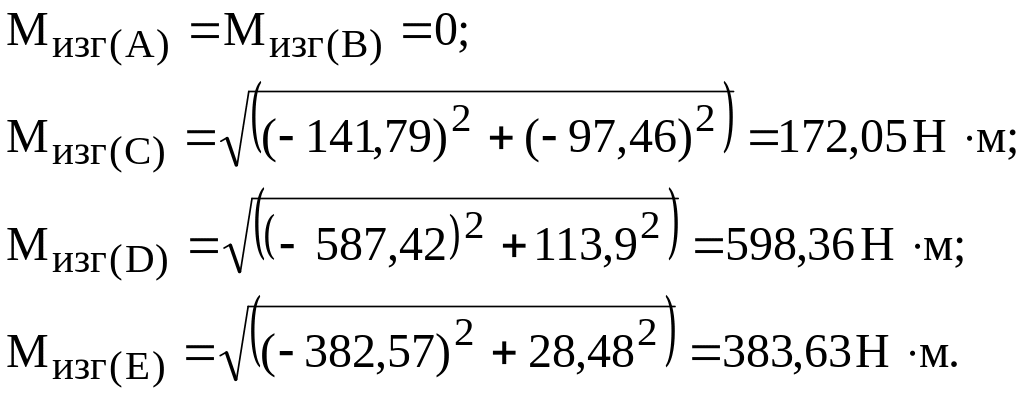
10 Из совместного рассмотрения эпюр крутящих и суммарных изгибающих моментов определяем опасное сечение. Таковым является сечение, где одновременно действуют наибольший изгибающий момент М_изг = 598,36 Н∙м и наибольший крутящий момент М_кр = 214,29 Н∙м.

11 Определяем значения приведенных (эквивалентных) моментов по третьей теории прочности (формула (1.8)):

.

12 Исходя из условия прочности определяем расчетное значение диаметра по третьей теории прочности (формулы (1.7) и (1.10)):

.

13 В соответствии с [1, таблица 7.1] принимаем диаметр вала d = 45 мм и проверяем его на прочность:

Вывод: в результате расчетов для заданной схемы нагружения был подобран вал диаметром 45 мм, обеспечивающий надежную работу конструкции с небольшим запасом прочности.

Рисунок 1.2 – К определению внутренних силовых факторов