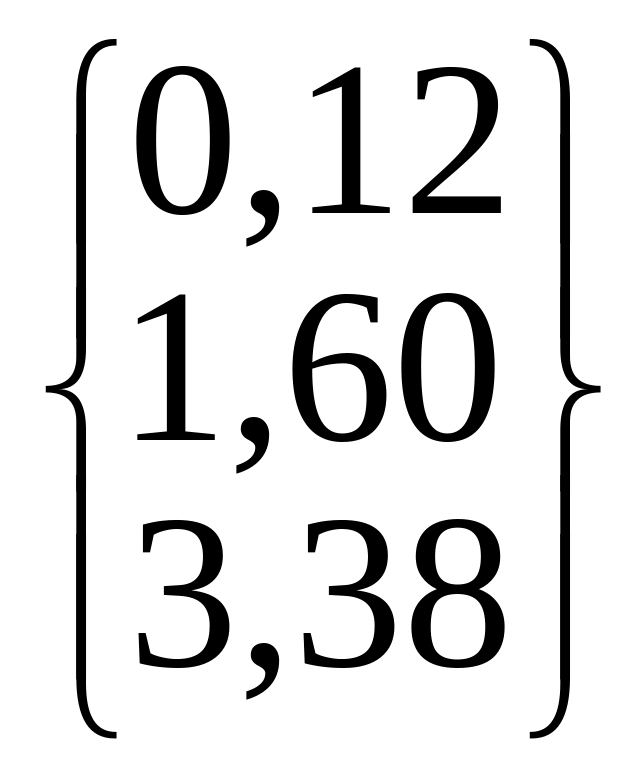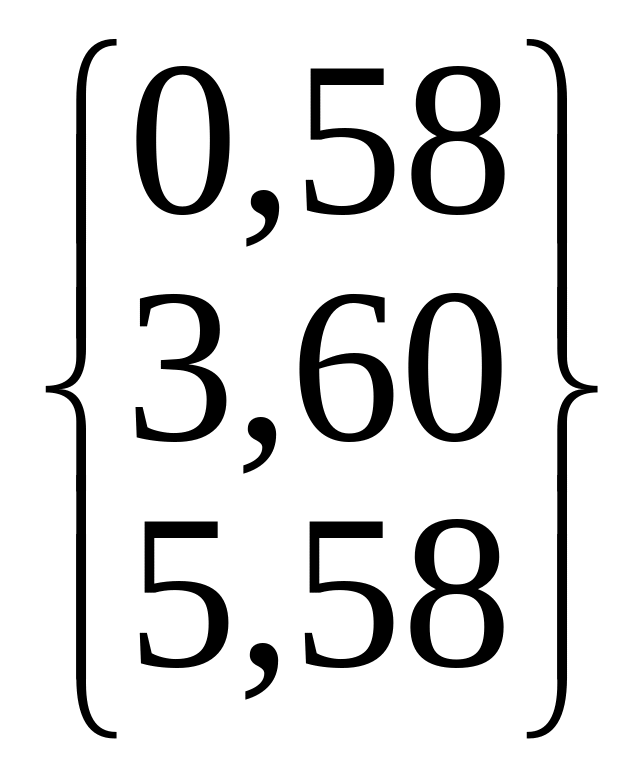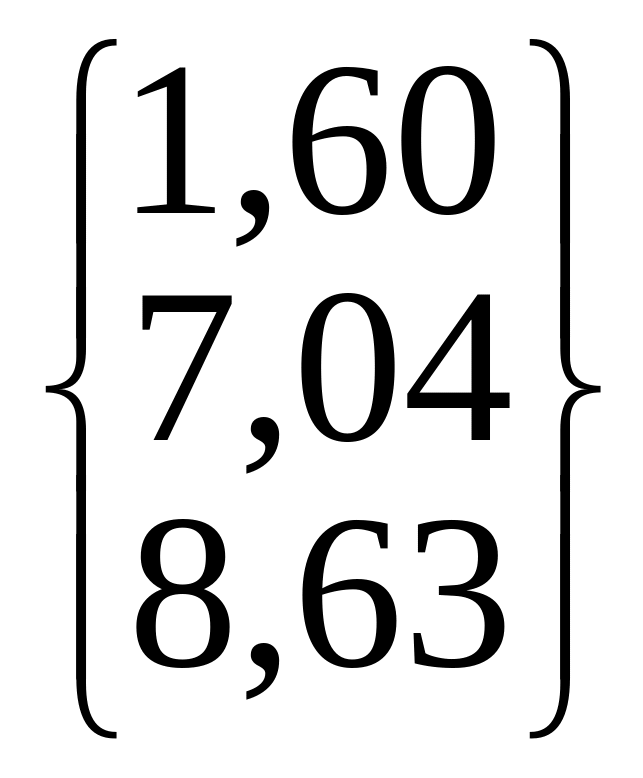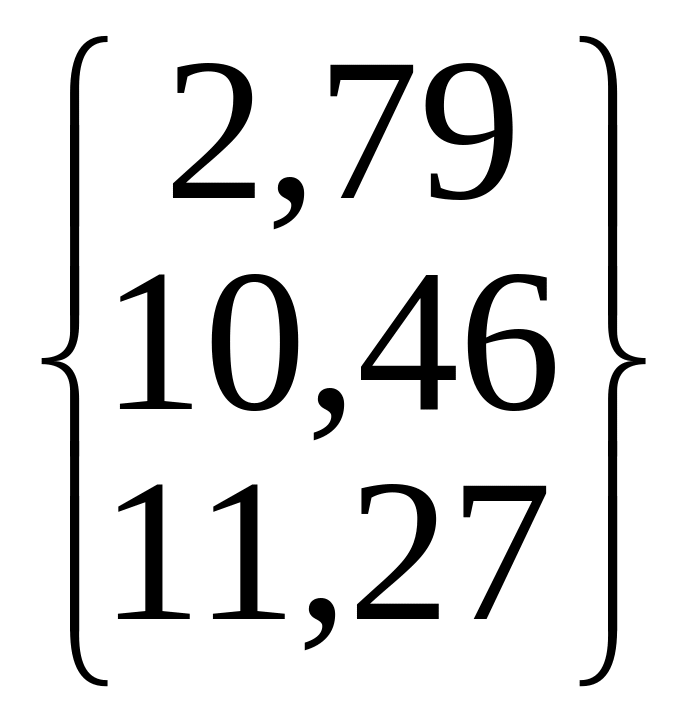Пример 7

Условия задачи: Построить график изменения осадки грунта во времени для полной стабилизированной осадки S ≈ 5 см, вычисленной в задаче 6 (методом эквивалентного слоя). Сжимаемая толща основания Н_с равна Н_с = 7,88 м, средний коэффициент относительной сжимаемости m_{v, ср} = 0,045 MПа^-1.

Значения коэффициентов фильтрации: для песка – 2·10^-4 см/c; для глины – 5·10^-9 см/c.

Решение

1) Выбираем расчетную схему для расчета затухания осадки во времени. Водопроницаемость грунтов с увеличением глубины уменьшается k_{f, 1} > k_{f, 2}, что соответствует схеме 3 в таблице 7.1. Путь фильтрации воды в данном случае равен мощности активной зоны h = Н_с = 7,88 м, ранее найденной в примере 6.

2) Воспользовавшись расчетной схемой, показанной на рисунке 6.1, по формуле (7.4) найдем средний коэффициент фильтрации

=

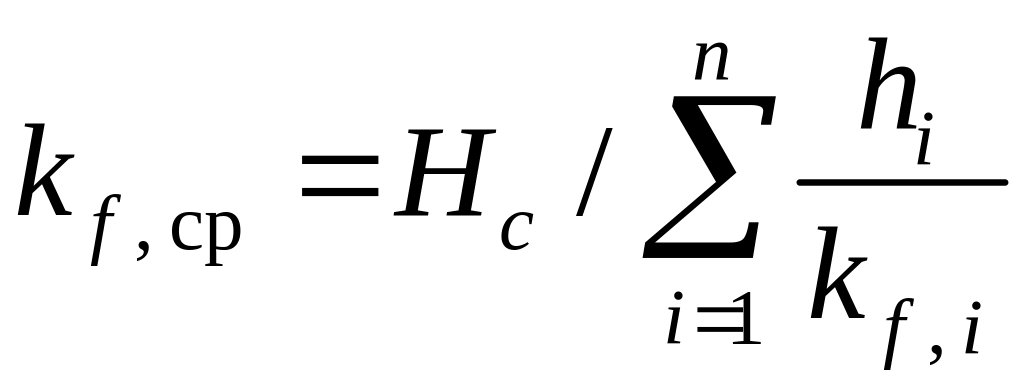= 7,88 / (3,5/(2·10^-4) + 4,38/(5·10^-9)) = 9·10^-9 см/c.

Для удобства расчета переведем полученное значение в м/год (1 см/c ≈ 3 · 10⁷ см/год = 3 · 10⁵ м/год): k_f, ср = 9 · 10^-9 см/c ≈ ≈ 2,7·10^-3 м/год.

3) Определим по формуле (7.3) средний коэффициент консолидации, учитывая, что γ_W ≈ 10⁴ Н/м³ и m_v, ср = 0,045 MПа^-1 = = 0, 045 ·10^-6 Н/м².

= 2,7·10^-3/(0,045·10^-6 ·10⁴) = 6 м²/год.

4) По формуле (7.5) получаем выражение для вычисления времени t, соответствующее заданной степени консолидации

= 4,2 · N года.

5) Дальнейшие расчеты оформим в виде таблицы 7.2. Задавшись последовательно значениями степени консолидации с шагом по 0,1U, из таблицы 7.1 выбираем соответствующее значение N (случай 3), для которого определяем время t. Достигнутая к этому времени осадка S_t вычисляется по формуле (7.1), учитывая значение полной стабилизированной осадки S = 5 см.

Таблица 7.2

U	N	t = 4,2·N, годы	, см
0,1	0,005	0,021	0,5
0,2	0,02	0,084	1
0,3	0,06	0,252	1,5
0,4	0,13	0,546	2
0,5	0,24	1,008	2,5
0,6	0,42	1,764	3
0,7	0,69	2,898	3,5
0,8	1,08	4,536	4
0,9	1,77	7,434	4,5
0,95	2.54	10,668	4,75
1	∞	∞	5

5) По результатам расчетов строим график изменения осадки грунта во времени (рисунок 7.2).

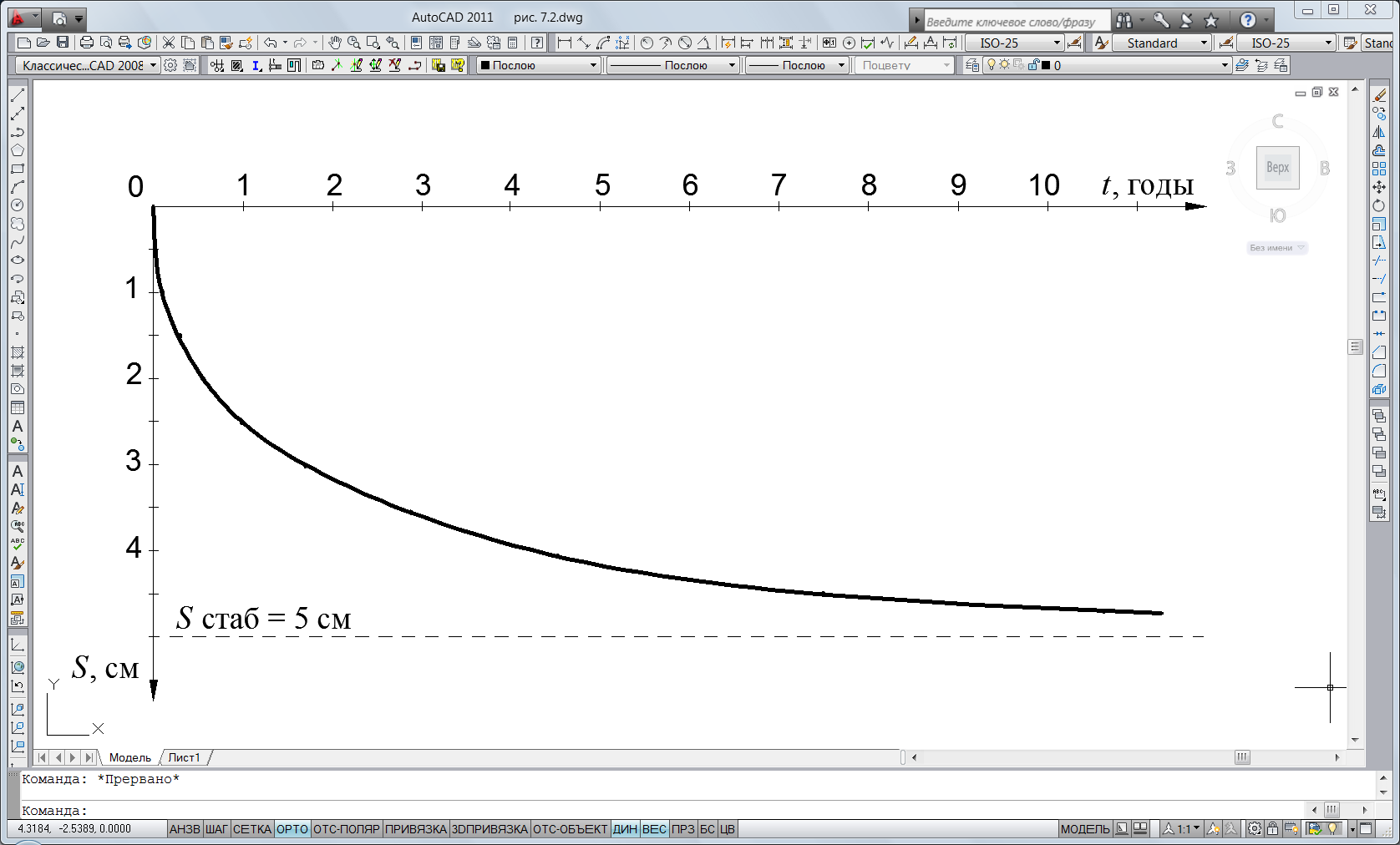
Рисунок 7.1 – График изменения осадки грунта во времени

Задача 8

определение критических нагрузок

на грунт основания

Анализируя фазы напряженного состояния грунтов, возникающие при постепенном загружении, можно выделить две критические нагрузки (рисунок 8.1):

– первая нагрузка, соответствующая началу возникновения в грунте зон сдвигов и окончания фазы уплотнения (начальная);

– вторая нагрузка, при которой под нагруженным фундаментом сформировываются сплошные области предельного равновесия, грунт приходит в неустойчивое состояние, исчерпывается его несущая способность (предельная).

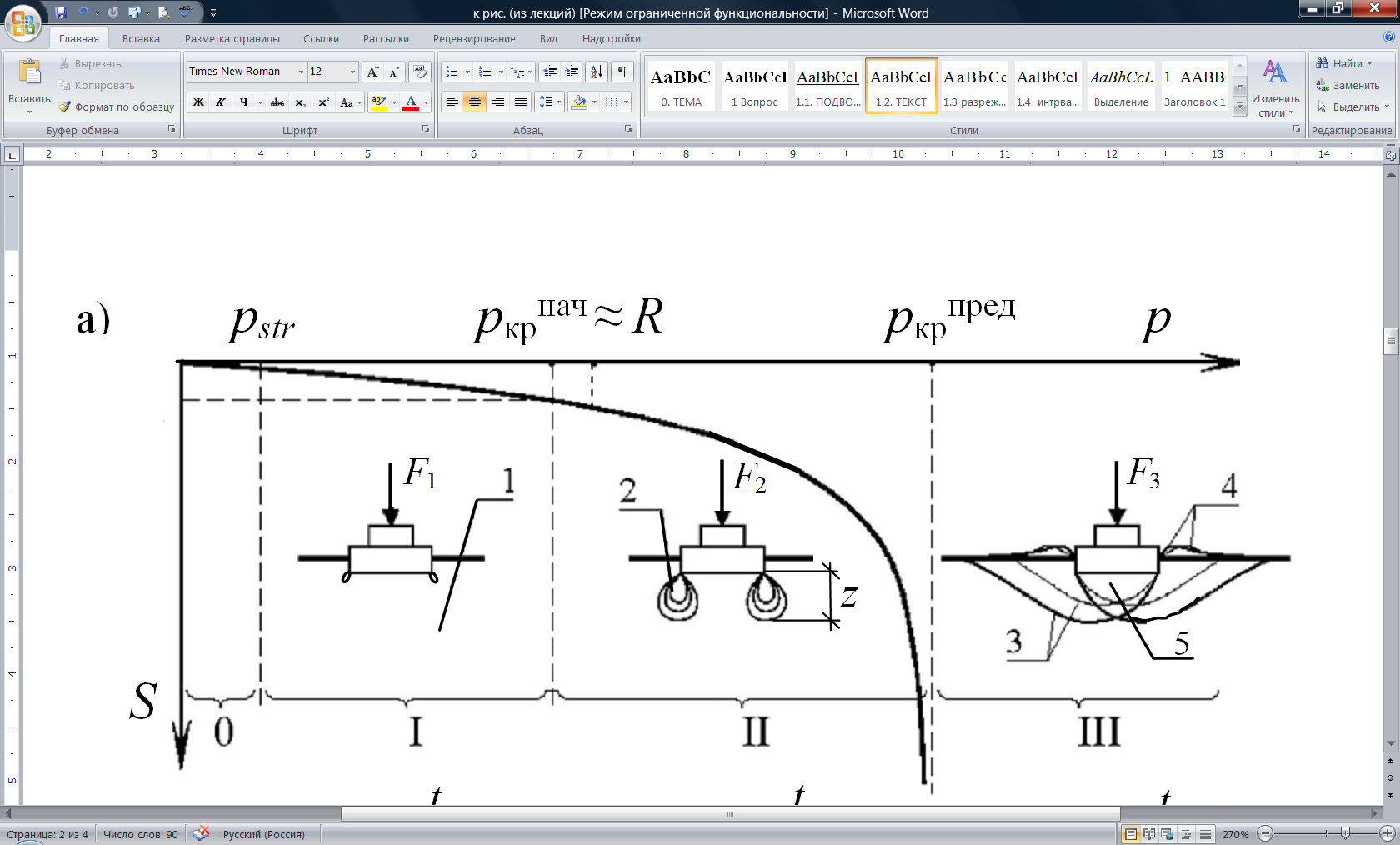
Рисунок 8.1 – Фазы напряженно-деформированного состояния грунта:

р_str – структурная прочность грунта; р_кр^нач – начальное критическое давление; р_кр^пред – предельное критическое давление; R – расчетное сопротивление грунта; 0 – фаза упругой работы; I – фаза уплотнения; II – фаза сдвигов; III – фаза выпоров; 1 – основание в докритическом состоянии; 2 – зоны сдвигов (пластических деформаций); 3 – линии скольжения; 4 – зоны выпоров; 5 – жесткое ядро; z – глубина развития зон сдвигов

1) Значение первой критической нагрузки на грунт может быть определено из уравнений предельного напряженного состояния грунтов по формуле

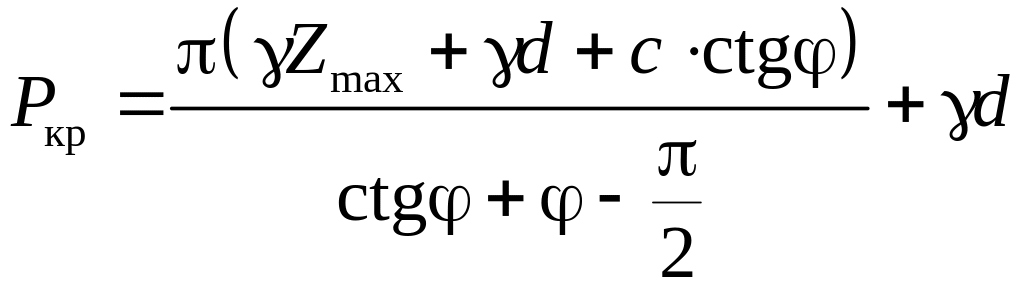, (8.1)

где d – глубина заложения фундамента;

γ – удельный вес грунта;

с – удельное сцепление грунта;

φ – угол внутреннего трения грунта;

Z_max – глубина развития областей предельного равновесия.

По определению, начальная критическая нагрузка соответствует случаю, когда в основании под подошвой фундамента ни в одной точке не возникает предельного состояния, т.е. в формуле (8.1) Z_max = 0. Формула для определения такой нагрузки впервые была получена Н.П. Пузыревским в 1923 г.

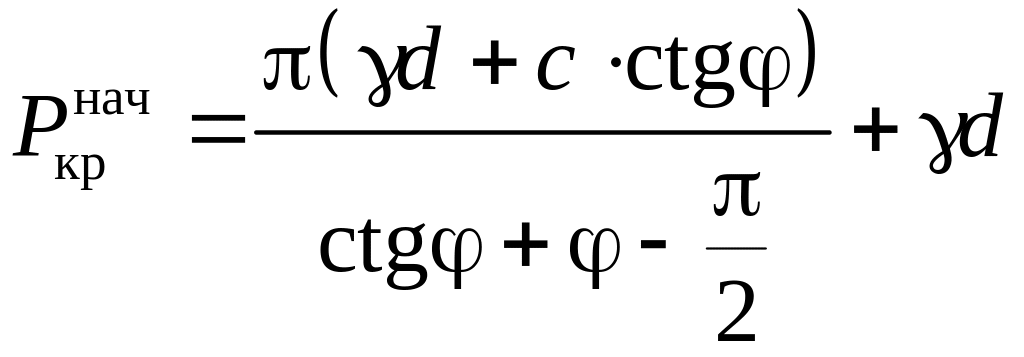. (8.2)

Строительные нормы СНиП 2.02.01 [6] допускают развитие пластических деформаций в краевых участках фундаментов на глубину Z_max = 0,25b (b – ширина подошвы фундамента). Тогда

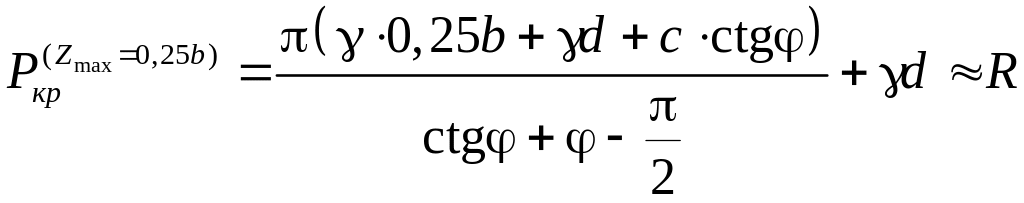, (8.3)

где R – расчетное сопротивление грунта основания, определяемое по формуле (7) СНиП 2.02.01[6].

Для практических инженерных расчетов формулу (8.3) изменили, введя коэффициенты совместности работы основания и сооружения (γ_с1, γ_с2) и табличные коэффициенты (M_γ, M_q, M_c), зависящие от угла внутреннего трения грунта (Таблица 8.1).

.

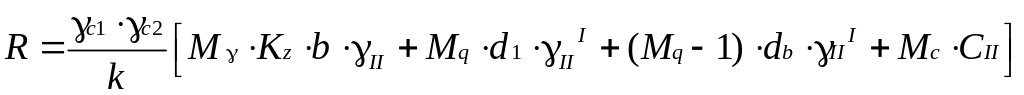Это выражение часто представляется в виде упрощенной трехчленной формулы

. (8.4)

2) Вторая – предельная критическая нагрузка р_u соответствует напряжению под подошвой фундамента, при котором происходит исчерпание несущей способности грунтов основания.

Впервые задача об определении предельной критической нагрузки для плоской задачи была решена в 1920 – 1921 гг. Л. Прандтлем и Г. Рейснером. в предположении невесомого основания (γ = 0). Ими было получено следующее выражение:

.

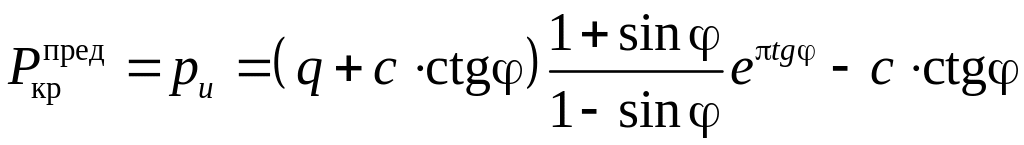Для практических расчетов чаще всего пользуются формулой предложенной В.В. Соколовским в 1952 г. для случая плоской задачи при действии на поверхности, наклоненной под углом δ к вертикали нагрузки q. В этом случае вертикальная составляющая предельной критической нагрузки р_u в любой точке загруженной поверхности с координатой х (по горизонтали) равна

, (8.5)

где N_γ, N_q, N_c – безразмерные коэффициенты несущей способности грунта основания, зависящие от угла внутреннего трения φ и угла наклона равнодействующей нагрузки q к вертикали δ, определяемые по таблице 8.2.

Строительные нормы СНиП 2.02.01 [6] для общего случая расчета вводят в формулу (8.7) коэффициенты формы подошвы фундамента (ξ_γ, ξ_q, ξ_с) и размеры его подошвы (b′ и l′) .

Таблица 8.1 – Значения коэффициентов M_γ, M_q, M_c

II, град.	Коэффициенты			II, град.	Коэффициенты			II, град.	Коэффициенты
	Mγ	Mq	Мc		Mγ	Mq	Мc		Mγ	Mq	Мc
0	0	1,00	3,14	16	0,36	2,43	4,99	31	1,24	5,95	8,24
1	0,01	1,06	3,23	17	0,39	2,57	5,15	32	1,34	6,34	8,55
2	0,03	1,12	3,32	18	0,43	2,73	5,31	33	1,44	6,76	8,88
3	0,04	1,18	3,41	19	0,47	2,89	5,48	34	1,55	7,22	9,22
4	0,06	1,25	3,51	20	0,51	3,06	5,66	35	1,68	7,71	9,58
5	0,08	1,32	3,61	21	0,56	3,24	5,84	36	1,81	8,24	9,97
6	0,10	1,39	3,71	22	0,61	3,44	6,04	37	1,95	8,81	10,37
7	0,12	1,47	3,82	23	0,69	3,65	6,24	38	2,11	9,44	10,80
8	0,14	1,55	3,93	24	0,72	3,87	6,45	39	2,28	10,11	11,25
9	0,16	1,64	4,05	25	0,78	4,11	6,67	40	2,46	10,85	11,73
10	0,18	1,73	4,17	26	0,84	4,37	6,90	41	2,66	11,64	12,24
11	0,21	1,83	4,29	27	0,91	4,64	7,14	42	2,88	12,51	12,79
12	0,23	1,94	4,42	28	0,98	4,93	7,40	43	3,12	13,46	13,37
13	0,26	2,05	4,55	29	1,06	5,25	7,67	44	3,38	14,50	13,98
14	0,29	2,17	4,69	30	1,15	5,59	7,95	45	3,66	15,64	14,64
15	0,32	2,30	4,84
Примечание – При промежуточных значениях II коэффициенты Mγ, Mq, Mc допускается определять по интерполяции.

Таблица 8.2 – Значения коэффициентов несущей способности N_, N_q, N_c

Угол внутрен-него грунта I, град	Обозна- чение коэффи-циентов	Коэффициенты несущей способности N, Nq, Nc при углах наклона к вертикали равнодействующей внешней нагрузки , град, равных
		0	5	10	15	20	25	30	35	40	45
1	2	3	4	5	6	7	8	9	10	11	12
0	N Nq Nc	0 1,00 5,14	-	-	-	-	-	-	-	-	-
5				/ = 4,9	-	-	-	-	-	-	-

Окончание таблицы 8.2

1	2	3	4	5	6	7	8	9	10	11	12
10	N Nq Nc	0,60 2,47 8,34	0,42 2,16 6,57		/=9,8	-	-	-	-	-	-
15	N Nq Nc	1,35 3,94 10,98	1,02 3,45 9,13	0,61 2,84 6,88		/=14,5	-	-	-	-	-
20	N Nq Nc	2,88 6,40 14,84	2,18 5,56 12,53	1,47 4,64 10,02	0,82 3,64 7,26		/=18,9	-	-	-	-
25	N Nq Nc	5,87 10,66 20,72	4,50 9,17 17,53	3,18 7,65 14,26	2,00 6,13 10,99	1,05 4,58 7,68		/=22,9	-	-	-
30	N Nq Nc	12,39 18,40 30,14	9,43 15,63 25,34	6,72 12,94 20,68	4,44 10,37 16,23	2,63 7,96 12,05	1,29 5,67 8,09		/=26,5	-	-
35	N Nq Nc	27,50 33,30 46,12	20,58 27,86 38,36	14,63 22,77 31,09	9,79 18,12 24,45	6,08 13,94 18,48	3,38 10,24 13,19		/=29,8	-	-
40	N Nq Nc	66,01 64,19 75,31	48,30 52,71 61,63	33,84 42,37 49,31	22,56 33,26 38,45	14,18 25,39 29,07	8,26 18,70 21,10	4,30 13,11 14,43		/=32,7	-
45	N Nq Nc	177,61 134,87 133,87	126,09 108,24 107,23	86,20 85,16 84,16	56,50 65,58 64,58	32,26 49,26 48,26	20,73 35,93 34,93	11,26 25,24 24,24	5.45 16,42 15,82		/=35,2
Примечания: 1. При промежуточных значениях I и  коэффициенты N, Nq, Nc допускается определять по интерполяции. 2. В фигурных скобках приведены значения коэффициентов несущей способности, соответствующие предельному значению угла наклона нагрузки /.

Для выполнения задачи № 8 необходимо выбрать исходные данные из таблицы А.5 приложения А. Выбор варианта задания производится по сумме последних трех цифр зачетки.