Пример 4

Условия задачи: Определить сжимающие напряжения от внешней нагрузки интенсивностью р = 300 кПа под центром и под серединой длинной стороны загруженного прямоугольника размером в плане 2 х 8 м на глубине z = 0; 0,5b; 1b и 2b от поверхности.

Решение

1) Вычислим нормальные сжимающие напряжения σ_zр под центром загруженной площади (точка О на рисунке 4.2, а) по формуле (4.1), где η = l/b = 8/2 = 4. Результаты заносим в таблицу 4.2 и на график (рисунок 4.2, б).

Таблица 4.2

№ точки, i	zi, м	 i = 2zi /b	αi (табл. 1)	σzр, i = αi·р , кПа
0	0	2·0/2 = 0	1	1· 300 = 300
1	0,5b = 1	2·1/2 = 1	0,815	0,815· 300 = 244
2	1b = 2	2·2/2 = 2	0,537	0,537· 300 = 161
3	2b = 4	2·4/2 = 4	0,264	0,264· 300 = 79

2) Вычислим нормальные сжимающие напряжения σ_zр для точки под серединой длинной стороны прямоугольной площади загрузки (точка С на рисунке 4.2, а). Разделим площадку на два прямоугольника размером 2 х 4 м так, чтобы рассматриваемая точка была бы угловой. Для каждого прямоугольника η = l/b = 4/2 = 2. Вычислим σ_zр, _с по формуле (4.2) сначала для одного прямоугольника, а затем их удвоим, так как фигуры имеют одинаковые размеры и интенсивность нагрузки. Результаты заносим в таблицу 4.3 и на график (рисунок 4.2, в).

Таблица 4.3

№ точки, i	zi, м	 i = zi /b	α i (табл. 1)	σzр, i = 0,25 αi ·р, кПа	2σzр, i, кПа
0	0	0/2 = 0	1	1· 0,25 · 300 = 75	150
1	0,5b = 1	1/2 = 0,5	0,949	0,949· 0,25 · 300 = 71	142
2	1b = 2	2/2 = 1	0,797	0,797· 0,25 · 300 = 60	120
3	2b = 4	4/2 = 2	0,477	0,477· 0,25 · 300 = 36	72

Результаты расчета в графической форме показаны на рисун- ке 4.2.

Рисунок 4.2 – Эпюры распределения напряжений в грунте

от действия равномерно-распределенной нагрузки

Задача 5

расчет осадки грунтов основания

методом послойного суммирования

Метод рекомендуется СНиП 2.02.01 «Основания зданий и сооружений» [6] в следующих случаях:

– ширина подошвы фундамента b < 10 м;

– в пределах сжимаемой толщи нет грунтов с модулем деформации Е ≥ 100 МПа.

Величину полной стабилизированной осадки грунтовой толщи S по методу послойного суммирования определяют как сумму осадок элементарных слоев грунта по формуле

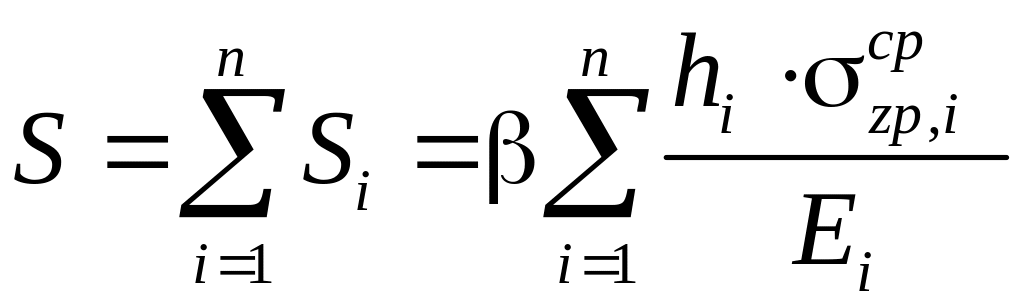, (5.1)

где β – безразмерный коэффициент, принимаемый для всех грунтов равным β = 0,8;

h_i – толщина элементарного слоя, принимаемая равной h_i ≤ 0,4 b, м;

– среднее напряжение в i-ом элементарном слое грунта, равное полусумме напряжений на верхней σ_zр, _i-1 и нижней σ_zр, _i границах этого слоя, кПа;

E_i – модуль общей деформации i-го элементарного слоя грунта, кПа;

п – число элементарных слоев грунта на которое разбита сжимаемая тоща H_c, толщина которой определяется в общем случае из условия (рисунок 5.1).

Порядок определения нормальных сжимающих напряжения от собственного веса грунта σ_zg и от внешней прямоугольной равномерно-распределенной нагрузки σ_zр был рассмотрен ранее в задачах 2 и 4.

Осадка вычисляется от действия дополнительных вертикальных напряжений р₀, определяемых на уровне подошвы фундамента по формуле

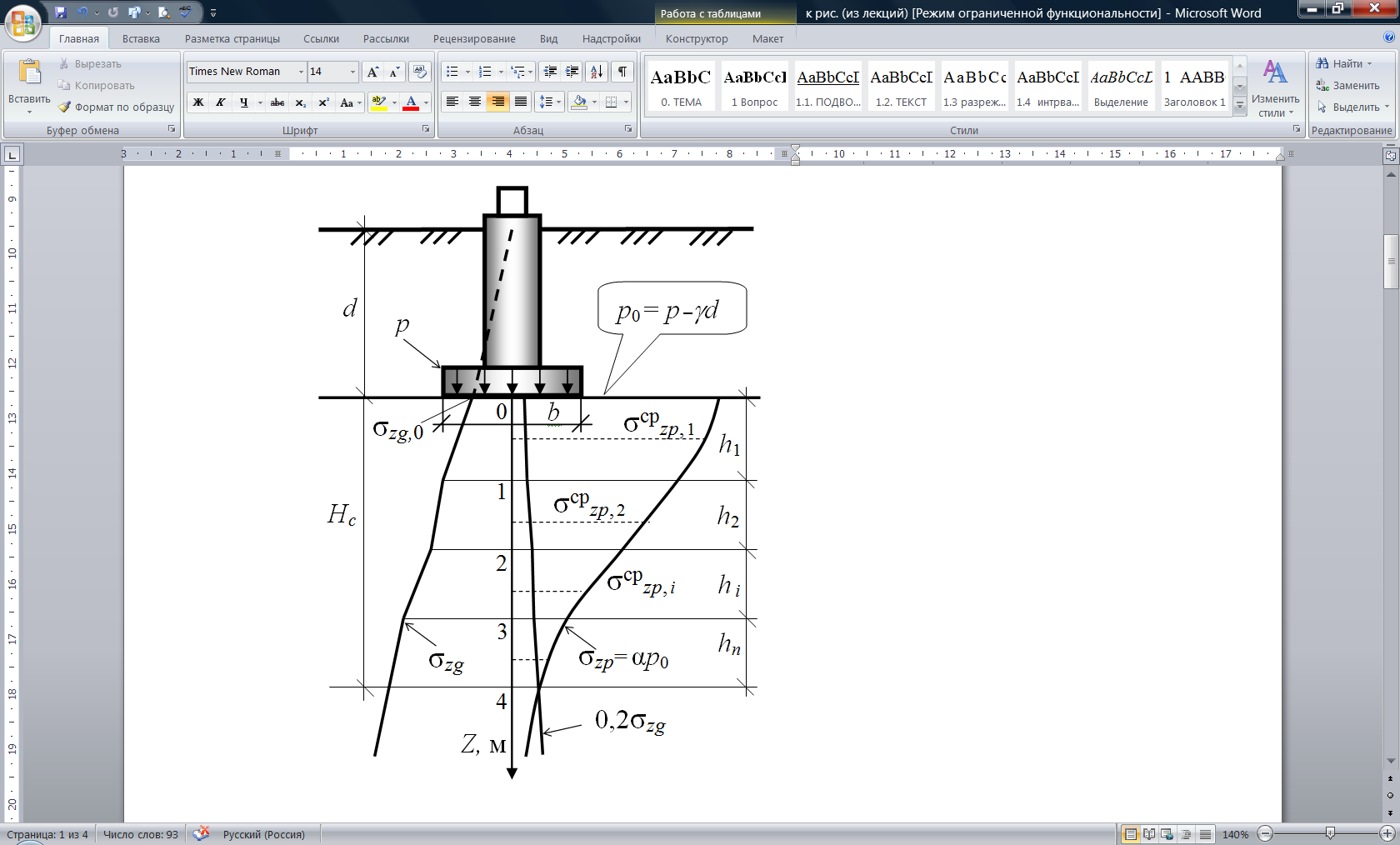
Рисунок 5.1 – Расчетная схема к определению осадки фундамента

методом послойно суммирования

Для выполнения задачи № 5 необходимо выбрать исходные данные из таблиц А.2 (грунты по схеме 2 – с грунтовыми водами) и А.4 (нагрузка) приложения А. Выбор варианта задания производится по сумме последних трех цифр зачетки. Глубина заложения фундамента d = 2 м (для четных вариантов) и d = 1,5 м (для нечетных вариантов).