Пример 10
Условия задачи: Подпорная стенка с абсолютно гладкими вертикальными гранями и горизонтальной поверхностью засыпки грунта с нагрузкой q = 30 кПа имеет размеры: высоту Н = 10 м; ширину низа (фундамента) b = 6 м, верха – а = 1,5 м; заглубление в основание d = 1,5 м, расположена в суглинистом грунте со следующими характеристиками: γ = 18 кН/м3, φ = 20º, с = 15 кПа.
Оценить устойчивость подпорной стены, определив аналитическим методом величины активного и пассивного давления грунта, построить их эпюры.
Решение
1) Определим высоту фиктивного слоя грунта h, заменяющего действие приложенной к поверхности нагрузки q = 30 кПа: h = = q/γ = 30/18 = 1,67 м.
2) По формуле (10.1) вычислим значения активного давления грунта σ2 на уровне верха и низа подпорной стены и построим эпюру их распределения.
При z = 0: = σ2,0 = = 18· (0 + 1,67) · tg2 (45 – 20/2) – 2·15· tg (45 – 20/2) = – 6,3 кПа (грунт не давит на стенку).
При z = Н: σ2,Н = 18· (10 + 1,67) · tg2(45 – 20/2) – 2·15· tg (45 – – 20/2) = 81,9 кПа.
Определим по формуле (10.2) положение нулевой ординаты h0, где σ2 = 0
= 2·15 / (18 · tg (45 – 20/2)) – 1,67 = 0,71 м.
Получили треугольную эпюру активного давления грунта (рисунок 10.2).
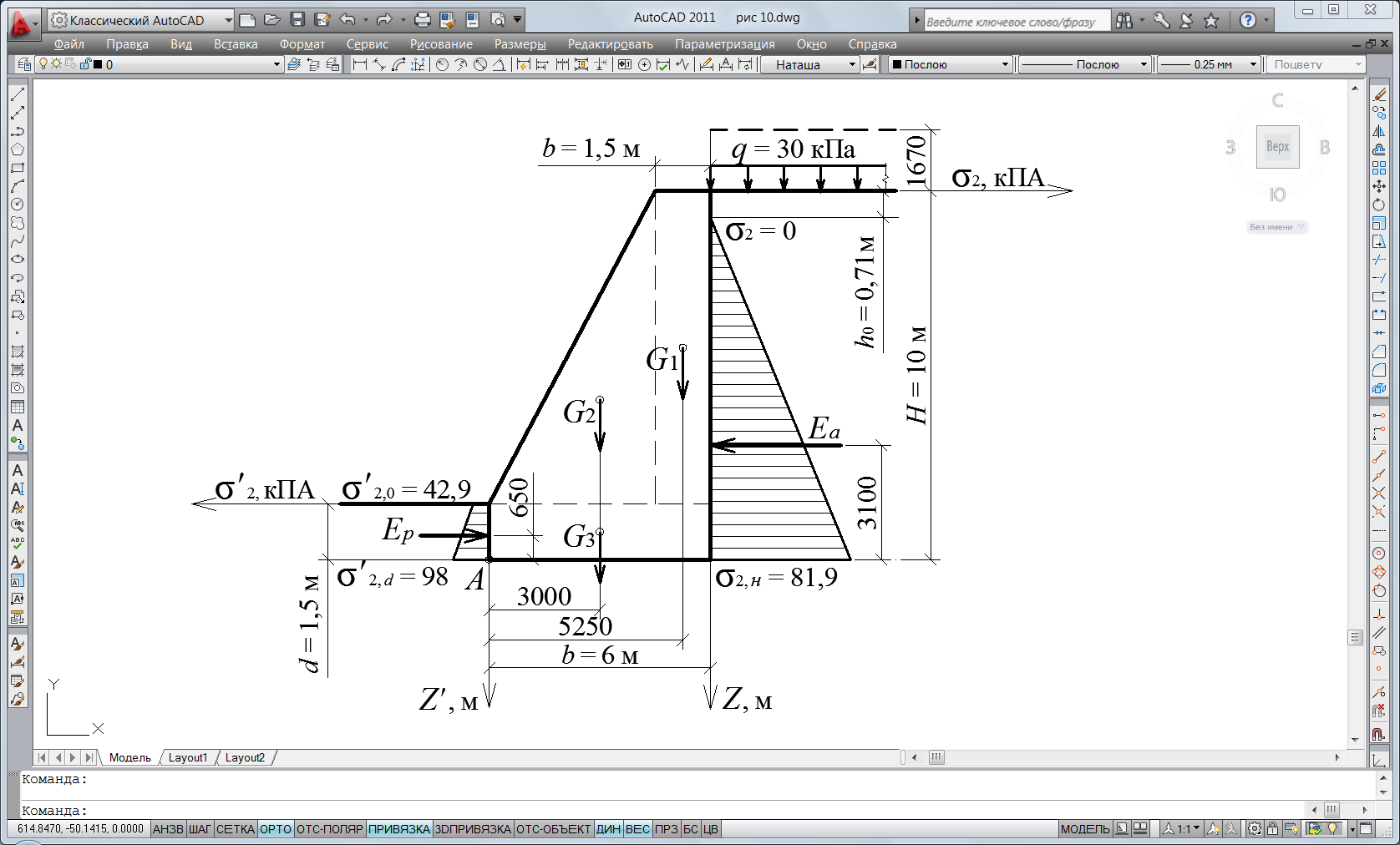
Рисунок 10.2 – Схема расчета к примеру 10
3) Вычислим по формуле (10.3) равнодействующую активного давления грунта на подпорную стенку Еа как площадь треугольной эпюры давлений
Еа = σ2, Н · (H – h0) / 2 = 81,9 · (10 – 0,71) / 2 = 380,4 кН.
Определим точку приложения равнодействующей Еа от подошвы фундамента стены еа по формуле (10.4) при треугольной эпюре давлений
еа = (H – h0)/3 = (10 – 0,71) /3 = 3,1 м.
4) По формуле (10.5) вычислим значения пассивного давления грунта σ2I на уровне верха и низа заглубления подпорной стены и построим эпюру их распределения.
При z I = 0: = σ2,0I = = 18·0·tg2 (45 + 20/2) + 2·15· tg (45 + 20/2) = 42,9 кПа.
При z I = d: σ2,d I = 18·1,5·tg2 (45 + 20/2) + 2·15· tg (45 + 20/2) = = 98 кПа.
Получаем трапецеидальную эпюру с площадью Ер, вычисляемую по формуле (10.6)
Ер
= (σ2,I0
+ σ2,Id)
·d
/ 2 =
=
0,5 ·18 ·1,52
·
tg2
(45
+ 20/2) +
+ 2·15·1,5· tg (45 + 20/2) = 105,6 кН.
Определим точку приложения равнодействующей Ер по формуле (10.7)
ер = (d/3) · (2·σ2,I0 + σ2,Id) / (σ2,I0 + σ2,Id) =
= (1,5/3) · (2·42,9 + 98) / (42,9 + 98) = 0,65 м.
5) Определим вес одного погонного метра подпорной стены, поделив ее на простые фигуры (рисунок 10.2) по формуле
G = G1 + G2 + G3 = γж.б · (V1 + V2 + V3) =
= 24·(1,5·8,5 + 4,5·8,5/2 + 1,5·6) = 981 кН,
где G1, G2, G3 – вес отдельных частей стенки, вычисляемый как Gi = γж.б · Vi,
γж.б – удельный вес материала стены, для железобетона равный γж.б = 24 кН/м3;
Vi – объемы i-ой части стены.
G1 = 24·(1,5·8,5) = 306 кН; G2 = 24·(4,5·8,5/2) = 459 кН;
G3 = 24·(1,5·6) = 216 кН.
6) Проверим устойчивость стены против опрокидывания относительно точки А по формуле (10.8).
∑Муд = ∑МG, i + Мр = ∑(Gi · еi) + Ер · ер = 306 · 5,25 + 459 · 3 + + 216 · 3 + 105,6 · 0,65 = 3700,14 кН·м.
∑Мопр = Ма = Еа · еа = 380,4 · 3,1 = 1179,24 кН·м.
kопр = ∑Муд / ∑Мопр = 3700,14 / 1179,24 = 3,14 > kнst = 1,5.
Стена на опрокидывание устойчива с достаточным запасом.
7) Проверим устойчивость стены на плоский сдвиг (по подошве) по формуле (10.9).
∑Fcдв = Еа = 380,4 кН.
∑Fуд = G·f + A·c + Ep = 981· 0,3 + 6 ·15 + 105,6 = 489,9 кН.
kсдв = ∑Fуд / ∑Fcдв = 489,9 / 380,4 = 1,29 < kнst = 1,3.
Устойчивость стены заданных размеров против сдвига не обеспечена, значит необходимо внести изменения в ее конструкцию.
Увеличиваем размер стены a до размера а I = 2 м, а заглубление d до d I = 2 м.
В этом случае ∑Fcдв = Еа = 380,4 кН будут иметь прежние значения.
Определим изменившиеся величины:
Ер = 0,5·18·22 · tg2 (45 + 20/2) + 2·15·2· tg (45 + 20/2) = 159,12 кН;
G = 24·(2·8 + 4·8/2 + 2·6) = 1056 кН
∑Fуд = 1056 · 0,3 + 6 ·15 + 159,12 = 565,9 кН.
kсдв = ∑Fуд / ∑Fcдв = 565,9 / 380,4 = 1,49 > kнst = 1,3.
Таким образом, изменение размеров стены обеспечивает устойчивость ее на сдвиг. Устойчивость стены на опрокидывание выполняется автоматически.