
- •Лекция по линейному программированию Введение. Предмет математического программирования
- •Запись задачи математического программирования
- •Классификация методов математического программирования
- •Линейное программирование Основная задача линейного программирования (злп)
- •Экономико-математические модели задач лп эмм планирования производства (задача о наилучшем использовании ресурсов)
- •Задача о смесях (выбор диеты, составление кормового рациона, приготовление различных смесей)
- •Формы записи злп
- •Взаимосвязь однородной и канонической форм записи
- •Следующие примеры дают представление о реализации указанных преобразований. Задача планирования производства в канонической форме
- •Задача о смесях в канонической форме
- •Графический метод решения злп
- •Симплексный метод линейного программирования Преобразование канонической модели в симплексную. Основная идея симплекс-метода
- •Алгоритм симплекс-метода
- •Теория двойственности в линейном программировании Построение двойственной злп
- •Исследование пары двойственных задач
- •Определение двойственных оценок злп
- •Экономическая интерпретация двойственных оценок
- •Устойчивость двойственных оценок
- •Транспортная задача Постановка транспортной задачи
- •Основные свойства тз
- •Методы построения первоначального плана
- •Метод северо-западного угла
- •Метод минимальной стоимости
- •Метод двойного предпочтения
- •Метод потенциалов получения оптимального плана тз Теорема о потенциалах
- •Алгоритм метода потенциалов
- •Другие типы транспортных задач Открытые мадели тз
- •В пунктах отправления имеются избыточные запасы тавара
- •Открытая модель тз с дефицитом ресурсов.
- •Тз с дополнительными требованиями
- •Тз с блокированием перевозок.
- •Ограничения типа .
- •Ограничения типа .
- •Транспортная задача по критерию времени
Алгоритм симплекс-метода
Этот алгоритм целесообразно рассмотреть на конкретном примере.
Пример. Решить симплекс-методом следующую ЗЛП:
|
(1) |
|
(2) |
|
(3) |
Эта задача относится к задаче об использовании ресурсов. Здесь в качестве свободных членов в правой части нетривиальных ограничений стоят запасы сырья трех видов. Такая задача удобна тем, что каноническая форма совпадает с симплексной, и не нужно прибегать к специальным приемам для её получения. Исходная задача в каноническом виде выглядит так:
|
(4) |
|
(5) |
|
(6) |
Систему отграничений-равенств можно записать в векторной форме
![]() +
+![]() +
+![]() +
+![]() +
+![]() =
=
![]() ,
,
где
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=
![]() ;
;
![]() =
=
![]() ;
;
![]() =
=
![]() ;
;
![]() =
=![]() .
.
Здесь векторы , и имеют предпочтительный вид, т.е. являются единичными в одном из компонентов и нулевыми во всех остальных компонентах. Вектор называется столбцом свободных членов системы ограничений.
Для решения задачи (4)-(6) симплекс - методом необходимо иметь опорный план, т.е. допустимое базисное решение системы (5). Для этого все векторы надо разделить на две группы – базисные и свободные. Сначала выбираем базисные. Поскольку нетривиальных ограничений всего три, то и базисных векторов будет тоже три. В качестве базисных выбирают вектора, имеющие предпочтительный вид, т.е. в данном случае , и . Им соответствуют базисные переменные х3, х4, х5 системы (5). Остальные переменные (х1 и х2 ) будут свободными. При получении базисного решения все свободные переменные приравниваются к нулю. Подставив в (5) х1= х2=0, легко получаем остальные компоненты опорного плана:
х3 = 400; х4 = 900; х5 = 600.
В векторном виде этот опорный план выглядит так:
![]() =
( 0 ; 0 ; 400 ; 900 ; 600 ).
=
( 0 ; 0 ; 400 ; 900 ; 600 ).
Подставив компоненты в целевую функцию (4), получим значение целевой функции для этого плана:
Z ( )=0.
Теперь составим первоначальную симплексную таблицу:
Сб |
Б |
0 |
60 |
40 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
||||
|
|
400 |
2 |
1 |
1 |
0 |
0 |
|
|
0 |
|
900 |
3 |
4 |
0 |
1 |
0 |
|
|
0 |
|
600 |
1 |
3 |
0 |
0 |
1 |
|
|
zj - cj |
0 |
- 60 |
- 40 |
0 |
0 |
0 |
|
||
В
верхней строке, над обозначениями
векторов, стоят коэффициенты целевой
функции при соответствующих переменных.
Нулевое значение над
![]() говорит о том, что свободный член в
целевой функции отсутствует. Нижняя
строка таблицы, которая называется
индексной
строкой,
содержит взятые с обратным знаком
значения коэффициентов из верхней
строки.
говорит о том, что свободный член в
целевой функции отсутствует. Нижняя
строка таблицы, которая называется
индексной
строкой,
содержит взятые с обратным знаком
значения коэффициентов из верхней
строки.
Второй столбец таблицы состоит из обозначений базисных векторов. Порядок, в котором они записаны, не случаен. Каждый вектор поставлен в той строке, где в столбце коэффициентов этого вектора находится единица. Слева от базисных векторов, в первом столбце таблицы, поставлены соответствующие коэффициенты целевой функции (из верхней строки).
Последний столбец рассмотрим позже.
Теперь, когда начальная таблица построена, известен соответствующий опорный план и значения целевой функции, нужно сделать вывод о том, можно ли улучшить целевую функцию. Ответ на этот вопрос дает содержимое индексной строки: в случае отсутствия там отрицательных чисел делается вывод о том, что достигнутый опорный план является оптимальным и целевую функцию нельзя увеличить, т.е. сделать больше. В противном случае целевую функцию можно улучшить. Поскольку в данном случае в индексной строке есть отрицательные числа, план не является оптимальным, и его можно улучшить.
Переход к новому, лучшему опорному плану называется итерацией симплекс-метода. Она представляет собой преобразование однократного замещения, поскольку при этом происходит переход к новому базису: один из базисных векторов становится свободным, а в базис, наоборот, входит один из бывших свободных векторов.
Найдем
эту пару векторов. Сначала определим
вектор, который войдет в базис. Это
должен быть один из свободных векторов,
т.е.
![]() или
или
![]() .
Выбираем тот вектор, которому в индексной
строке соответствует самое отрицательное
число (-60, обведено пунктиром). Значит,
вектор
.
Выбираем тот вектор, которому в индексной
строке соответствует самое отрицательное
число (-60, обведено пунктиром). Значит,
вектор
![]() становится базисным.
становится базисным.
Теперь
определим вектор, “покидающий” базис.
Это делается с помощью симплексных
отношений,
обозначенных в последнем столбце
симплекс–таблицы. Как видно из заголовка
столбца, числителем симплексного
отношения является свободный член
ограничения, а знаменателем –
положительные
коэффициенты ведущего
столбца,
т.е. столбца
(вектора, который теперь войдет в базис).
Строка, в которой находится минимальное
симплексное отношение, называется
ведущей
строкой.
В той же строке находится вектор
![]() ,
покидающий наш первоначальный базис.
Только при этом условии гарантируется
неотрицательность свободных членов
при пересчете таблицы. Отметим также,
что при
,
покидающий наш первоначальный базис.
Только при этом условии гарантируется
неотрицательность свободных членов
при пересчете таблицы. Отметим также,
что при
![]() симплексные отношения являются
недопустимыми или не существуют; их не
следует рассматривать при определении
минимального отношения.
симплексные отношения являются
недопустимыми или не существуют; их не
следует рассматривать при определении
минимального отношения.
Элемент таблицы, находящийся на пересечении ведущего столбца и ведущей строки, называется ведущим элементом таблицы (он обозначен сплошным квадратом).
Теперь приступим к пересчету таблицы. Это делается в три этапа. Сначала ведущая строка делится на ведущий элемент:
Сб |
Б |
0 |
60 |
40 |
0 |
0 |
0 |
|
|
|
|
|
|
||
60 |
|
200 |
1 |
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
zj - cj |
|
|
|
|
|
|
|
Обратите внимание, что во втором столбце вместо уже стоит новый базисный вектор с коэффициентом 60 в столбце Сб.
Далее
впишем в эту таблицу столбцы новых
базисных векторов. При этом, поскольку
![]() и
и
![]() остались в базисе, их столбцы остаются
без изменений, а столбец
становится точно таким же, каким до
этого был
:
остались в базисе, их столбцы остаются
без изменений, а столбец
становится точно таким же, каким до
этого был
:
Сб |
Б |
0 |
60 |
40 |
0 |
0 |
0 |
|
|
|
|
|
|
||
60 |
|
200 |
1 |
|
|
0 |
0 |
0 |
|
|
0 |
|
|
1 |
0 |
0 |
|
|
0 |
|
|
0 |
1 |
zj - cj |
|
0 |
|
|
0 |
0 |
|
Наконец, на третьем этапе определим значения в оставшихся девяти клетках таблицы. Их нужно пересчитать по правилу прямоугольника.
Чтобы сформулировать это правило, снова посмотрим на первоначальную симплекс-таблицу. Обратите внимание, что оставшиеся неизвестными элементы новой таблицы в первоначальной таблице соответствуют элементам, стоящим наискосок к ведущему элементу (поскольку ведущая строка и ведущий столбец уже построены).
Для любого элемента первоначальной таблицы можно определить прямоугольник




 а*
В
а*
В
А а
Здесь
![]() -
ведущий элемент, а
- искомый
элемент, А, В – элементы, находящиеся с
ними на пересечении строк и столбцов.
-
ведущий элемент, а
- искомый
элемент, А, В – элементы, находящиеся с
ними на пересечении строк и столбцов.
Н овое
значение элемента а
получается из формулы:
овое
значение элемента а
получается из формулы:
![]()
Это и есть правило прямоугольника.
Например, для прямоугольника, обозначенного в первоначальной таблице, в новой таблице получаем значение:
0
-
![]() = -
= -
Все остальные значения пересчитываются аналогично. Получаем таблицу первой итерации симплекс-метода:
Сб |
Б |
0 |
60 |
40 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|||
60 |
|
200 |
1 |
|
|
0 |
0 |
|
|
|
300 |
0 |
|
- 1,5 |
1 |
0 |
|
0 |
|
400 |
0 |
|
- |
0 |
1 |
|
|
12000 |
0 |
- 10 |
30 |
0 |
0 |
|
|
Произошел
переход к новому базису:
![]() ,
,![]() ,
,![]() .
При этом переменные х2,
х3 являются
свободными, и в опорном плане их значения
равны нулю. Значения остальных переменных
получаем из нового столбца свободных
членов:
.
При этом переменные х2,
х3 являются
свободными, и в опорном плане их значения
равны нулю. Значения остальных переменных
получаем из нового столбца свободных
членов:
х1 = 200; х4 = 300; х5 = 400.
Запишем опорный план в векторной форме:
![]() =
( 200 ; 0 ; 0 ; 300 ; 400 ).
=
( 200 ; 0 ; 0 ; 300 ; 400 ).
Этому плану соответствует значение целевой функции, равное 12000 (проверьте подстановкой компонент в выражение (4)). В новой таблице это значение зафиксировано в индексной строке в столбце свободных членов.
Как
видим, в индексной строке остался один
отрицательный элемент, поэтому полученный
план не является оптимальным. Значение
-10 находится в столбце
![]() ,
поэтому
войдет в новый базис. Минимальное
симплексное отношение достигается в
строке базисного вектора
,
который выходит из базиса.
,
поэтому
войдет в новый базис. Минимальное
симплексное отношение достигается в
строке базисного вектора
,
который выходит из базиса.
Теперь пересчитываем таблицу первой итерации и получаем таблицу второй итерации:
Сб |
Б |
0 |
60 |
40 |
0 |
0 |
0 |
|
|
|
|
|
|
||
60 |
|
140 |
1 |
0 |
4/5 |
- 1/5 |
0 |
40 |
|
120 |
0 |
1 |
- 3/5 |
2/5 |
0 |
0 |
|
100 |
0 |
0 |
1 |
- 1 |
1 |
zj - cj |
13200 |
0 |
0 |
24 |
4 |
0 |
|
Аналогично определяем новый опорный план:
![]() =
( 140 ; 120 ; 0 ; 0 ; 100 ).
=
( 140 ; 120 ; 0 ; 0 ; 100 ).
Ему соответствует значение целевой функции, равное 13200. Поскольку в индексной строке уже нет отрицательных элементов, план является оптимальным:
![]() ;
;
![]() =13200.
=13200.
Итак, задача линейного программирования решена.

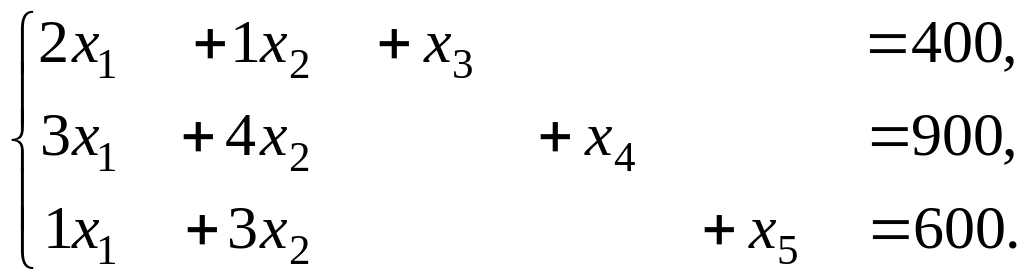
 0
0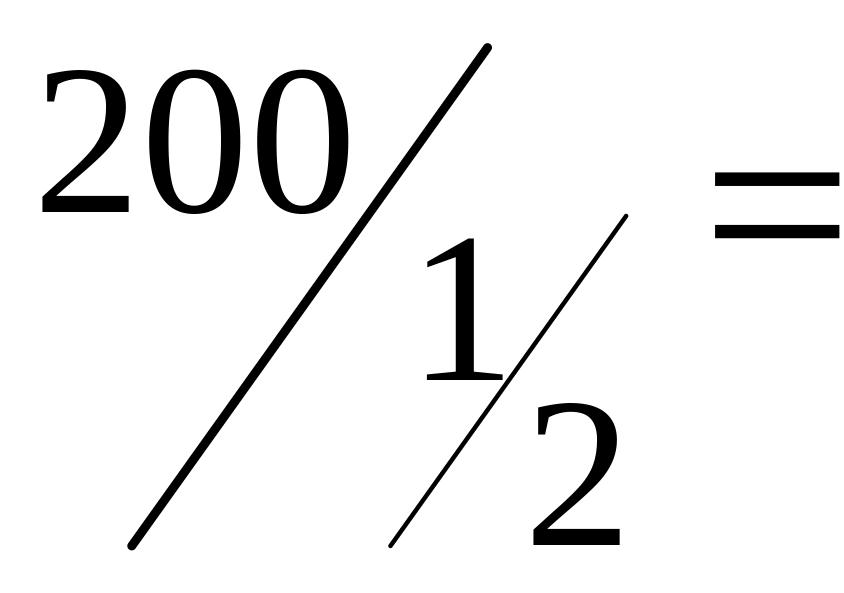 400
400 0
0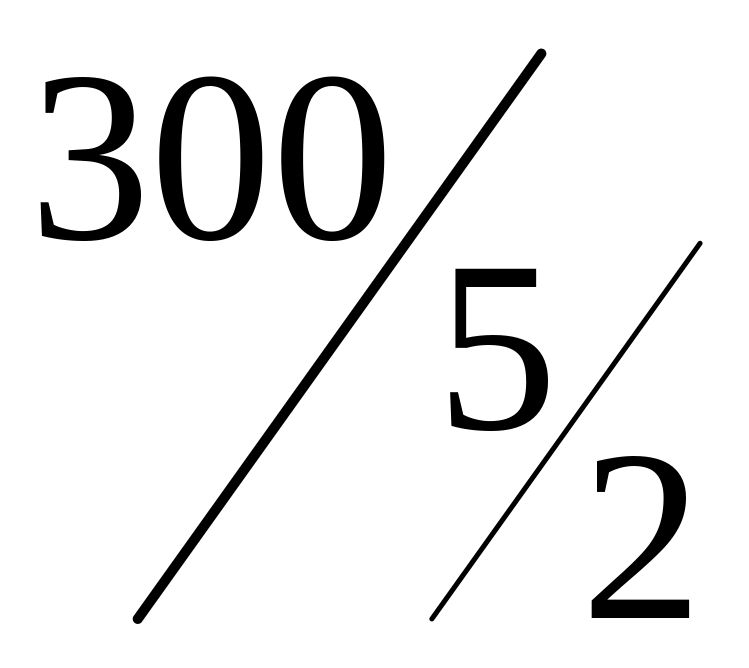 =120
=120 160
160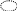 zj
- cj
zj
- cj