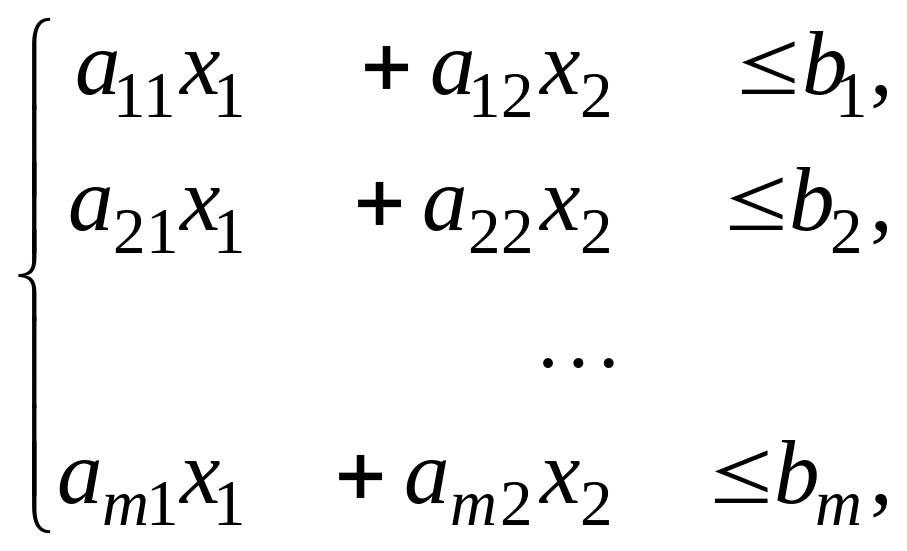Взаимосвязь однородной и канонической форм записи

Общая ЗЛП может быть с помощью эквивалентных преобразований приведена сначала к однородной, а затем к канонической форме. Рассмотрим этот процесс более подробно.

Перевод общей ЗЛП в однородную форму. Основным отличием общей формы от однородной является наличие в составе ограничений некоторого количества уравнений вида (7); каждое такое уравнение

эквивалентно системе из двух нестрогих неравенств

Эквивалентные преобразования однородной модели в каноническую.

1. Каждое исходное неравенство типа «меньше или равно» приводится к эквивалентной системе из уравнения и тривиального неравенства добавлением своей балансовой переменной:

(x_n+1 – балансовая переменная)

2. Каждое исходное неравенство типа «больше или равно» приводится к эквивалентной системе из уравнения и тривиального неравенства вычитанием своей балансовой переменной:

, (x_n+2 – балансовая переменная)

Поскольку новые переменные вводятся от каждого неравенства, размерность задачи возрастает.

3. Если на какую-нибудь переменную не наложено условие неотрицательности, её можно представить как разность двух неотрицательных переменных:

4. Если , то это требование эквивалентно требованию 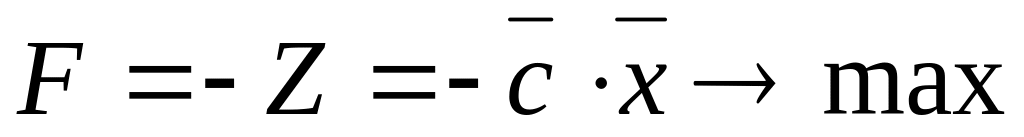, то есть при необходимости задачу минимизации можно заменить задачей максимизации и наоборот.

5. Дополнительные балансовые переменные вводятся в целевую функцию с коэффициентами, равными нулю:

Следующие примеры дают представление о реализации указанных преобразований. Задача планирования производства в канонической форме

Задача о смесях в канонической форме

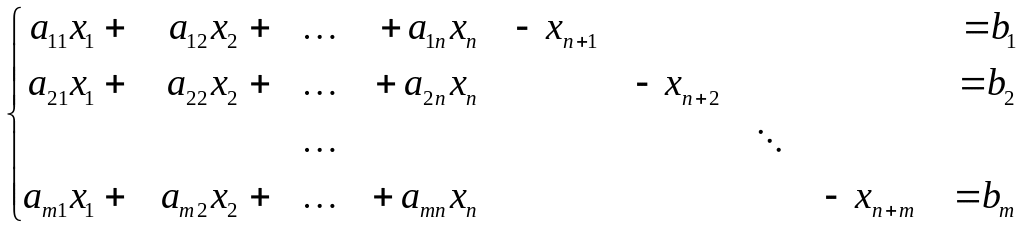
Пример. Привести ЗЛП к канонической форме:

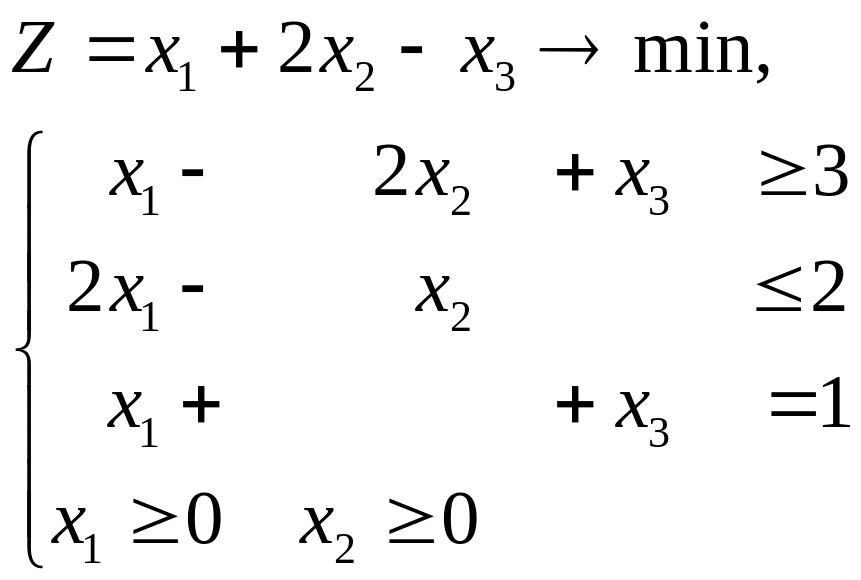
Обратите внимание, что переменная x₃ может принимать произвольные значения.

Решение. Поскольку на переменную x₃ не наложено условие неотрицательности, заменим её разностью двух неотрицательных переменных . Для удобства, чтобы не было штрихов, переобозначим эти переменные соответственно . Введём балансовые переменные Подставим новые переменные в выражение для целевой функции и в нетривиальные ограничения задачи, дополнив при этом тривиальные ограничения новыми переменными, получим:

Графический метод решения злп

Графический метод используется, с одной стороны, для обобщения на алгебраический метод с произвольным количеством переменных, с другой стороны, для наглядного представления решения ЗЛП с двумя переменными. При наличии только двух переменных область допустимых решений (ОДР) может быть легко изображена на плоскости .

Рассмотрим ЗЛП с двумя переменными в однородной форме записи:

	(1)
	(2)
	(3)

Рассмотрим вектор , который называется градиентом функции Z. Его компонентами являются частные производные целевой функции по соответствующим координатам, которые по своему смыслу представляют собой скорости возрастания функции Z вдоль осей Ox₁ и Ox₂ соответственно. Этот вектор показывает направление наискорейшего возрастания целевой функции. Вектор называется антиградиентом целевой функции, он показывает направление наискорейшего убывания целевой функции. Выберем произвольное значение целевой функции Z=Z₀. Получим уравнение прямой Z₀=c₁x₁+c₂x₂ в системе координат . Эту прямую также называют линией уровня целевой функции, то есть линией постоянного значения. Положим Z₀=0, получаем линию уровня, проходящую через начало координат. При Z>Z₀ линия уровня будет лежать параллельно первоначальной дальше от начала координат в направлении вектора . Очевидно, что все линии уровня параллельны между собой и, соответственно, перпендикулярны векторам - планам задачи.

При этом оптимальному решению задачи будет отвечать такой допустимый план задачи, который лежит на линии уровня, находящейся как можно дальше от начала координат.

Рассмотрим вектор роста целевой функции на плоскости

Т еперь рассмотрим нетривиальные ограничения (2) и запишем их в виде:

(4)

Множество решений (4) представляет собой полуплоскость, расположенную по одну из сторон прямой, уравнение которой:

(5)

Другими словами, эта прямая представляет собой границу полуплоскости. Если построить на плоскости все полуплоскости из системы (4), а затем учесть все тривиальные неравенства (3), которые локализуют допустимые решения ЗЛП в первом квадранте системы координат, то получим область, которая называется областью допустимых решений (ОДР) ЗЛП. Эта область на плоскости, если она является ограниченной, имеет вид выпуклого многоугольника. В общей теории линейного программирования доказывается, что ОДР представляет собой выпуклую область, то есть область, в которой любые две точки соединяются отрезком прямой, полностью лежащим в этой области. Важным следствием этого положения является тот факт, что оптимальное решение ЗЛП, если оно существует, обязательно будет находиться в угловой точке ОДР (в одной или в нескольких). Теперь, подводя итог всему сказанному, можно утверждать, что оптимальное решение ЗЛП находится в той угловой точке, из которой на направление вектора роста целевой функции опускается самый дальний от начала координат перпендикуляр. После нахождения оптимальной угловой точки надо найти её координаты как пересечение соответствующих границ, это будет оптимальный план. Далее определяем значение целевой функции в оптимальной точке, подставляя в эту функцию найденные координаты.

Пример. Решить графически следующую ЗЛП:

Построим, например, полуплоскость, отвечающую первому неравенству системы (1):

2x₁ + 1x₂ ≤ 400.

Эта полуплоскость делит координатную плоскость граничной линией, заданной уравнением:

2x₁ + 1x₂ = 400.

Линию, если она не проходит через начало координат, проще всего построить по двум точкам на осях координат. При х₁= 0 получаем х₂ = 400, а при х₂ = 0 получаем х₁ = 200. Соединяем эти две точки прямой линией, получаем две полуплоскости, выше и ниже этой прямой. Исходному неравенству отвечает только одна из этих полуплоскостей. Она определяется подстановкой в неравенство пробной точки, не лежащей на граничной прямой. Например, такой точкой может быть начало координат х₁ = х₂ = 0, т.е. 0  400.

Это неравенство является истинным, значит, начало координат принадлежит указанной полуплоскости. В противном случае пробная точка лежит в полуплоскости, не отвечающей исходному неравенству.

Аналогично построим и две другие полуплоскости, получим ОДР:

Теперь надо найти угловую точку ОДР, в которой целевая функция достигает максимума. Для этого построим вектор роста целевой функции = ( 60 ; 40 ), который состоит из коэффициентов целевой функции при соответствующих переменных. Вектор роста указывает направление наискорейшего возрастания целевой функции. Надо найти в ОДР точку, наиболее удаленную от начала координат в этом направлении. Для этого на направление вектора из всех угловых точек ОДР опускаем перпендикуляры. Оптимальному плану соответствует угловая точка, порождающая самый дальний от начала координат перпендикуляр. В нашем случае такая угловая точка образована пересечением границ 1-го и 2-го неравенств, поэтому эти неравенства запишутся как уравнения:

Решение этой системы даёт оптимальный план первоначальной задачи:

= 140; = 120.

Этот план дает значение целевой функции, равное 13200:

Таким образом, решение исходной задачи получено.

Теперь рассмотрим другие частные случаи ОДР на плоскости.

1. О ДР представляет собой не ограниченную в направлении вектора роста целевой функции многоугольную область. В этом случае оптимального решения не существует, целевая функция стремится к бесконечности:

2. ОДР состоит из единственной точки. Этот случай встречается крайне редко, и тогда задача имеет единственное допустимое решение, которое является одновременно оптимальным

3. О ДР- пустое множество. В этом случае система ограничений задачи противоречива, и задача вообще не имеет допустимых, а следовательно, и оптимальных решений.

4. З адача имеет бесконечное множество оптимальных решений. Это происходит, когда две угловые точки ОДР являются оптимальными; следовательно, оптимальными являются и все точки, лежащие на участке границы между этими угловыми точками.

Замечание. Графическим методом можно решить ЗЛП и с большим числом неизвестных, если в её канонической записи число неизвестных n и число линейно независимых уравнений m связаны соотношением:

так как в этом случае методом исключения Жордана - Гаусса можно перейти к двум переменным. Решая эту задачу графически, находят две компоненты оптимального плана. Подставляя их в ограничения задачи, определяют и остальные компоненты.