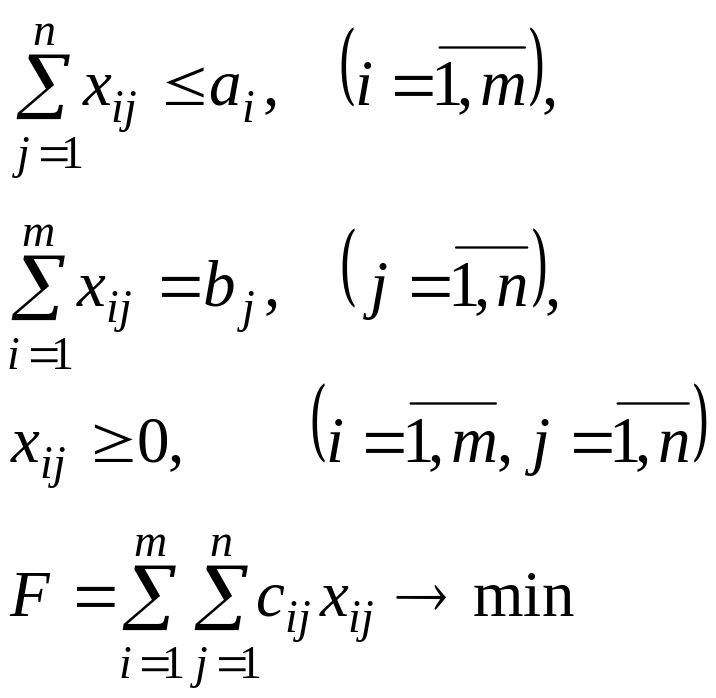- •Лекция по линейному программированию Введение. Предмет математического программирования
- •Запись задачи математического программирования
- •Классификация методов математического программирования
- •Линейное программирование Основная задача линейного программирования (злп)
- •Экономико-математические модели задач лп эмм планирования производства (задача о наилучшем использовании ресурсов)
- •Задача о смесях (выбор диеты, составление кормового рациона, приготовление различных смесей)
- •Формы записи злп
- •Взаимосвязь однородной и канонической форм записи
- •Следующие примеры дают представление о реализации указанных преобразований. Задача планирования производства в канонической форме
- •Задача о смесях в канонической форме
- •Графический метод решения злп
- •Симплексный метод линейного программирования Преобразование канонической модели в симплексную. Основная идея симплекс-метода
- •Алгоритм симплекс-метода
- •Теория двойственности в линейном программировании Построение двойственной злп
- •Исследование пары двойственных задач
- •Определение двойственных оценок злп
- •Экономическая интерпретация двойственных оценок
- •Устойчивость двойственных оценок
- •Транспортная задача Постановка транспортной задачи
- •Основные свойства тз
- •Методы построения первоначального плана
- •Метод северо-западного угла
- •Метод минимальной стоимости
- •Метод двойного предпочтения
- •Метод потенциалов получения оптимального плана тз Теорема о потенциалах
- •Алгоритм метода потенциалов
- •Другие типы транспортных задач Открытые мадели тз
- •В пунктах отправления имеются избыточные запасы тавара
- •Открытая модель тз с дефицитом ресурсов.
- •Тз с дополнительными требованиями
- •Тз с блокированием перевозок.
- •Ограничения типа .
- •Ограничения типа .
- •Транспортная задача по критерию времени
Другие типы транспортных задач Открытые мадели тз
В пунктах отправления имеются избыточные запасы тавара
В
этом случае
![]() .
.
Экономико-математическая модель такой ТЗ также является ЗЛП:
|
(8) |
Обратите внимание, что вместо уравнений (1) в модели (8) появились неравенства, означающие, что не все товары будут вывезены с баз.
Введение дополнительных (балансовых) переменных в эти неравенства для получения каконического вида модели эквивалентно введению (n+1)-го заказчика (фиктивного заказчика) с заявкой:
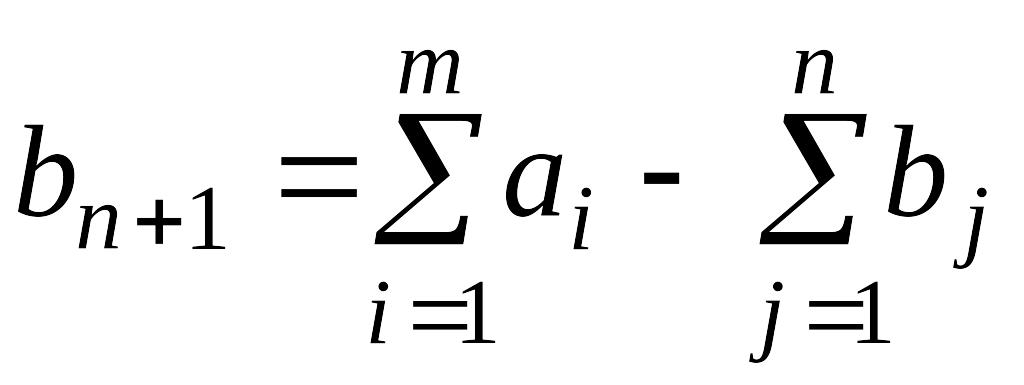
и
нулевыми тарифами перевозок к нему от
каждого поставщика
![]() .
В транспортной таблице модифицированной
задачи появляется дополнительный
столбец, в каждой клетке которого
вписываются нулевые тарифы. Таким
образом, получаем закрытую модель ТЗ.
Эта задача решается обычными методами,
рассмотренными выше. Смысл полученных
в решении значений балансовых переменных
здесь-остатки грузов на базах. Другими
словами, в некоторых клетках дополнительного
столбца после оптимального решения
остаются ненулевые значения перевозок
(фиктивные значения); значит, с
соответствующих баз не вывезены остатки
товаров.
.
В транспортной таблице модифицированной
задачи появляется дополнительный
столбец, в каждой клетке которого
вписываются нулевые тарифы. Таким
образом, получаем закрытую модель ТЗ.
Эта задача решается обычными методами,
рассмотренными выше. Смысл полученных
в решении значений балансовых переменных
здесь-остатки грузов на базах. Другими
словами, в некоторых клетках дополнительного
столбца после оптимального решения
остаются ненулевые значения перевозок
(фиктивные значения); значит, с
соответствующих баз не вывезены остатки
товаров.
Открытая модель тз с дефицитом ресурсов.
В
этом случае
![]() .
ЭММ имеет вид:
.
ЭММ имеет вид:
 (9)
(9)
Обратите внимание на то, что вместо системы уравнений (2) записана система неравенств. Вводим фиктивного поставщика с номером (n+1) и запасом груза в нем, равным:
![]()
В
транспортной таблице появится
дополнительная строка с номером (m+1),
в каждую клетку которой ставим нулевой
тариф:
![]() .
Перевозки в этих клетках являются
балансовыми переменными. В результате
получаем закрытую модель ТЗ и решаем
её обычными методами. При этом в
оптимальном решении некоторые из
дополнительных клеток обязательно
будут заполнены ненулевыми значениями
перевозок. Смысл этих значений-недополученный
груз соответствующими заказчиками.
.
Перевозки в этих клетках являются
балансовыми переменными. В результате
получаем закрытую модель ТЗ и решаем
её обычными методами. При этом в
оптимальном решении некоторые из
дополнительных клеток обязательно
будут заполнены ненулевыми значениями
перевозок. Смысл этих значений-недополученный
груз соответствующими заказчиками.
Тз с дополнительными требованиями
Тз с блокированием перевозок.
В некоторых случаях реальных перевозок
отдельные маршруты отсутствуют. В этом
случае в соответствующие клетки таблицы
ставят очень большие тарифы, которые
обозначают М:
некоторых случаях реальных перевозок
отдельные маршруты отсутствуют. В этом
случае в соответствующие клетки таблицы
ставят очень большие тарифы, которые
обозначают М:
Тогда в результате решения ТЗ все клетки без перевозок в оптимальное решение не попадут.
Ограничения типа .
В этом случае на отдельных маршрутах
предписываются конкретные объёмы
перевозок. Исходная транспортная задача
модифицируется так: в клетках, где
зафиксированы объёмы перевозок,
пересекаются некоторые базы и заказчики;
из заявок этих заказчиков и из запасов
на этих базах вычитаются величины
этом случае на отдельных маршрутах
предписываются конкретные объёмы
перевозок. Исходная транспортная задача
модифицируется так: в клетках, где
зафиксированы объёмы перевозок,
пересекаются некоторые базы и заказчики;
из заявок этих заказчиков и из запасов
на этих базах вычитаются величины
![]() ,
а вклетки ставят очень большие тарифы
М. Далее решается обычная транспортная
задача. В результате решения в нужных
клетках будут нулевые перевозки.
Окончательный план образуется вписыванием
заданных величин в исключенные клетки.
,
а вклетки ставят очень большие тарифы
М. Далее решается обычная транспортная
задача. В результате решения в нужных
клетках будут нулевые перевозки.
Окончательный план образуется вписыванием
заданных величин в исключенные клетки.
Ограничения типа .
На отдельных маршрутах объёмы перевозок должны быть не меньше некоторого минимального уровня. Модификация задачи и её решения в общем виде можно представить на следующей схеме:

Дополнительное требование типа
 ,
то есть
от iго
поставщика к j-му
потребителю можно вывести не более ij
единиц груза (более сложная схема
изменения ТЗ).
,
то есть
от iго
поставщика к j-му
потребителю можно вывести не более ij
единиц груза (более сложная схема
изменения ТЗ).
Задача
модифицируется так: заявка некоего
фиктивного потребителя фиксируется на
уровне ij,
а остальная часть заявки j-го
потребителя
![]() помещается
в дополнительный
столбец.
В этот же дополнительный столбец вносятся
те же тарифы, что и в j-й
столбец, кроме клетки в i-й
строке, куда записывают бесконечно
большой тариф М.
Таким образом, вместо одного столбца
для соответствующего потребителя
появляются два, отвечающие за неких
фиктивных потребителей, суммарная
заявка которых равна заявке прежнего
заказчика. В результате при решении
модифицированной задачи в одном из
дополнительных столбцов ни в одной
клетке перевозка не превысит величину
ij,
поскольку вся заявка этого столбца и
равна этой величине, а в другом столбце
в соответствующей клетке вообще не
будет перевозок, так как клетка имеет
тариф М. В результате при пересчете
суммарные перевозки двух фиктивных
поставщиков в соседних клетках равны
их суммам, а в нужной клетке общая
перевозка не превысит предельную
величину (ведь вторым слагаемым здесь
будет нулевое значение перевозки!).
помещается
в дополнительный
столбец.
В этот же дополнительный столбец вносятся
те же тарифы, что и в j-й
столбец, кроме клетки в i-й
строке, куда записывают бесконечно
большой тариф М.
Таким образом, вместо одного столбца
для соответствующего потребителя
появляются два, отвечающие за неких
фиктивных потребителей, суммарная
заявка которых равна заявке прежнего
заказчика. В результате при решении
модифицированной задачи в одном из
дополнительных столбцов ни в одной
клетке перевозка не превысит величину
ij,
поскольку вся заявка этого столбца и
равна этой величине, а в другом столбце
в соответствующей клетке вообще не
будет перевозок, так как клетка имеет
тариф М. В результате при пересчете
суммарные перевозки двух фиктивных
поставщиков в соседних клетках равны
их суммам, а в нужной клетке общая
перевозка не превысит предельную
величину (ведь вторым слагаемым здесь
будет нулевое значение перевозки!).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cij xij |
|
|
|
Cij xij |
M 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bj |
|
|
|
|
|
|