3.6. Особенности движения автомобиля по криволинейному продольному профилю

На современных автомобильных дорогах участки, имеющие различные продольные уклоны, сопрягают вставкой вертикальных кривых больших радиусов. В условиях пересеченного рельефа местности протяженность вертикальных кривых иногда превышает 50% общей длины дорог высших категорий.

При движении автомобиля по криволинейному продольному профилю преодолеваемый продольный угол непрерывно изменяется, в связи с чем меняется и скорость автомобиля. Это делает условными выводы, вытекающие из рассмотренных выше формул движения с «равновесными скоростями». Поэтому в уравнении движения автомобиля для случая криволинейного продольного профиля сопротивление движению на подъем должно быть принято переменным (рис. 3.15).

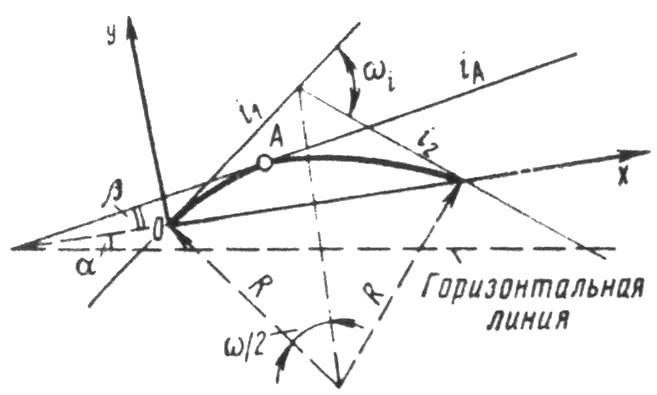
Рис. 3.15. Схема к выводу уравнения движения автомобиля по вертикальным кривым

Решения для движения автомобиля по криволинейному продольному профилю были предложены А. Е. Вельским и К. А. Хавкиным. Вертикальные кривые на автомобильных дорогах обычно разбивают по квадратичной параболе

, (3.24)

аппроксимирующей круговую кривую. Знак «–» относится к выпуклым кривым, знак «+» – к вогнутым.

Если расположить начало координат в начале выпуклой вертикальной кривой в точке О таким образом, чтобы ось х совпадала с хордой вертикальной кривой, то уравнение вертикальной кривой будет иметь вид

. (3.25)

Уклон в некоторой точке А на кривой

, (3.26)

где a – угол наклона к горизонту хорды, стягивающей вертикальную кривую и являющейся одной из осей координат; – угол наклона касательной к вертикальной кривой по отношению к хорде (оси х), меняющийся по длине кривой.

Согласно рис. 3.15 внешний угол перелома проектной линии w=i₁+i₂, угол наклона хорды к горизонтали

. (3.27)

Углы a, b и w должны быть выражены в радианах.

Подставляя найденное значение a в уравнение (3.26), получаем, что уклон в точке А

. (3.28)

При выводе этой формулы в связи с малыми значениями продольных уклонов, допускаемых на автомобильных дорогах, пренебрегали разностью в длинах, измеряемых для одной и той же точки по хорде и ее горизонтальной проекции.

Правые части кривых на графиках динамических характеристик за точкой максимума могут быть выражены уравнением вида

, (3.29)

где G – вес автомобиля, Н; V – скорость автомобиля, м/с; а, b – параметры, характеризующие зависимость силы тяги от скорости движения на разных передачах и при разной степени открытия дроссельной заслонки.

Параметры а и b определяют подбором по графикам кривых динамических характеристик. Их можно получить и расчетом исходя из уравнения внешней характеристики двигателя. Значения параметров а, b и m для случая движения некоторых автомобилей на прямой передаче при полном открытии дроссельной заслонки и при полной нагрузке автомобиля приведены в табл. 3.6.

Таблица 3.6. Значения параметров а, b и m

Автомобиль	а, Н	b, Н×с2/м2	m, 1/м
ЗИЛ-114	2590	1,94	4,9×10-4
ГАЗ-24 «Волга»	2130	0,8	4,1×10-4
ВАЗ-2101	1330	0,45	3,1×10-4
«Москвич-412»	3120	1,9	3,2×10-4
ЗИЛ-130	4370	4,5	3,0×10-4
КамАЗ-5320	4400	3,1	4,0×10-4

Подставляя в основное уравнение динамического фактора автомобиля (3.18) значения переменного продольного уклона и уравнение динамической характеристики (3.29), получаем исходное дифференциальное уравнение для определения скоростей движения по выпуклому криволинейному продольному профилю

. (3.30)

Решение дифференциального уравнения с учетом того, что , а также с учетом начального условия, что при x=0 скорость V_x равна начальной скорости V_н (в м/с), развитой в конце предшествующего участка, приводит к выражению

, (3.31)

где (см. табл. 3.4); е – основание натурального логарифма; k₁ и k₂ – коэффициенты, определяемые по формулам , .

Для выпуклых кривых в формуле (3.31) следует принимать верхние знаки, для вогнутых кривых – нижние. Начальный продольный уклон i принимают для подъемов со знаком «+», для спусков – со знаком «–».

Поскольку в выражения (3.29), (3.30) и (3.31) входит вес автомобиля G, уравнение (3.31) может быть использовано для расчетов скоростей движения автопоездов и автомобилей при разной степени загрузки.