Xlabel('Відносна частота збудження'), ylabel('Амплітуда (градуси)')
а) б)
в) г)
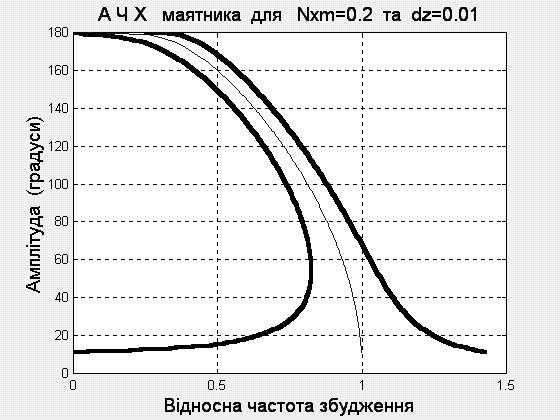
д) e)
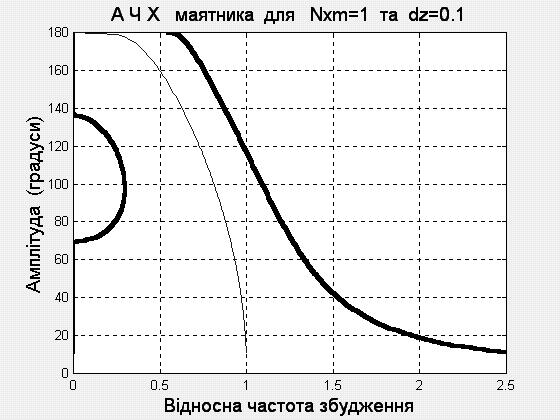
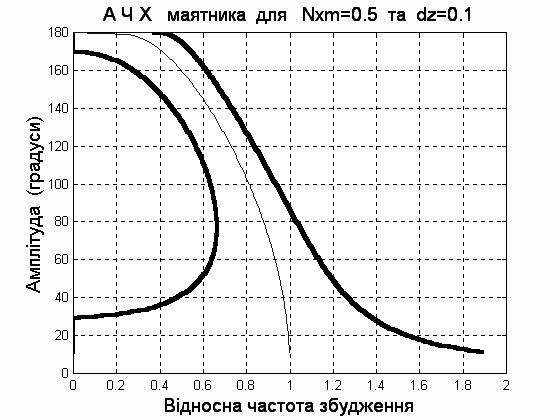
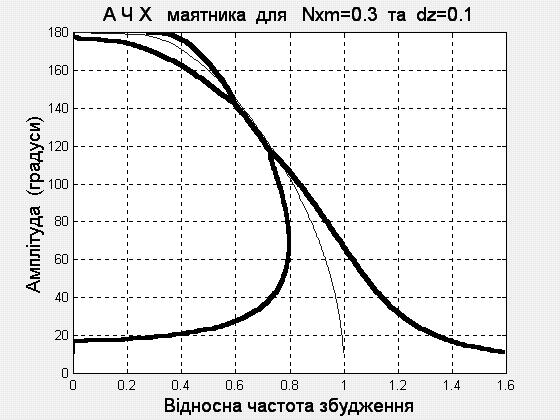
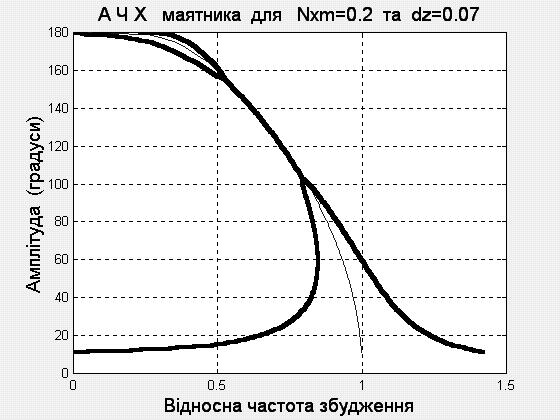
Рис. 1. 3. АЧХ маятника за різних умов
На рис.
1.3 відображені отримані графіки. Рис.
1.3, а...1..3, г презентують АЧХ при значенні
відносного коефіцієнта згасання
0,1
і різних значеннях амплітуди вібрації
точки підвісу (
1;
0,5; 0,3 і 0,2 відповідно). На рис. 1.3, д
і 1.3, е подано АЧХ при
0,2
і
0,07
і 0,01.
1.2.4. Завдання
Амплітуду перевантаження і відносний коефіцієнт загасання обрати з таблиці 1.1 згідно свого варіанту.
Таблиця 1.1
-
Варіант
1
1
0.01
2
0.3
0.01
3
0.5
0.01
4
0.8
0.1
5
0.8
0.05
6
1
0.05
7
0.5
0.05
8
0.8
0.01
9
1
0.1
10
0.3
0.1
11
0.5
0.1
12
0.3
0.05
1.2.5. Методичні вказівки до виконання
Коли коливання маятника з часом не встановлюються, цю обставину слід фіксувати, а при побудові графіка, відмічати у середині відповідної зони частот характер руху маятника (обертання, зростання амплітуди коливань, загасання коливань).
1.2.6. Контрольні запитання
Які коливання нелінійної системи називають вимушеними?
Які особливості мають АЧХ нелінійних систем у порівнянні з АЧХ лінійної стаціонарної системи?
Які особливості мають АЧХ маятника?
Яку роль у графіку АЧХ відіграє скелетна крива?
За яких умов АЧХ нелінійної системи наближається до скелетної кривої?
По яких формулах і за яким алгоритмом обчислені побудовані на рис. 1.3 теоретичні АЧХ вимушених коливань маятника? Яку при цьому обрано залежність частоти власних коливань від їхньої амплітуди?
У чому полягає сутність метода лінеаризації відшукування розв’язків нелінійних диференціальних рівнянь?