3.1.2.1. Вільний рух дгк

Вільний рух двоступеневий гірокомпас здійснює у випадку, коли основа рухається по поверхні Землі з постійною швидкістю ( , ), а вдовж вимірювальній осі не діють моменти сил. Тоді і , і рівняння (3.9) набуває вигляду:

. (3.11)

Положення рівноваги можна визначити, якщо у рівнянні (3.11) покласти прискорення рівним нулю (рис. 3.3):

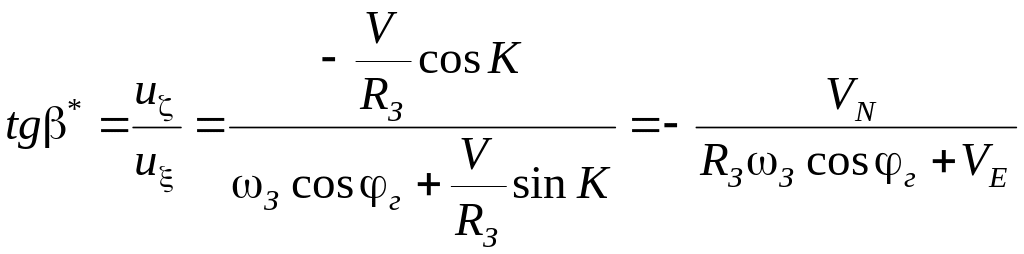. (3.12)

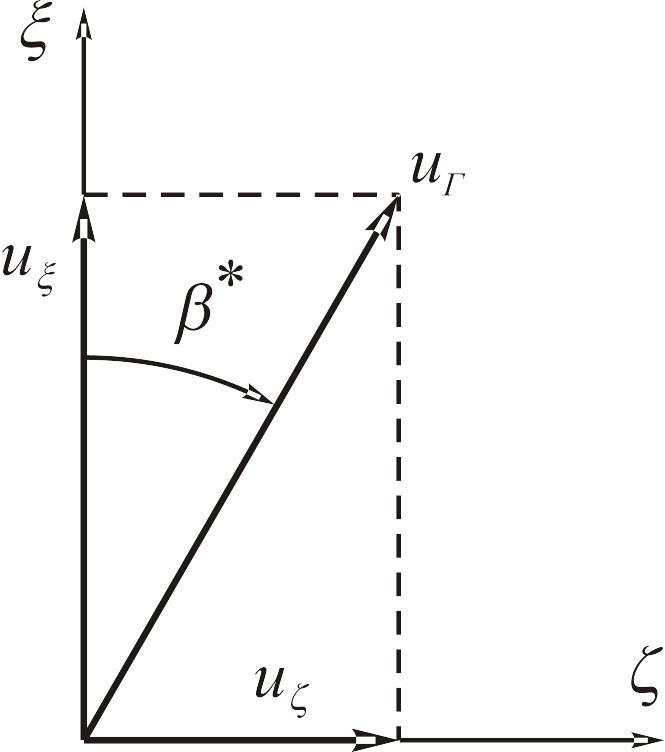
Рис. 3.3. До визначення швидкісної похибки гірокомпаса

Це положення рівноваги характеризує так звану швидкісну похибку гірокомпаса.

Якщо основа не переміщується по поверхні Землі ( ), то швидкісна похибка відсутня, а рівняння (3.11) при малих відхиленнях від меридіану ( ) набуває вигляду

. (3.13)

Розв’язок цього рівняння є таким

, (3.14)

де

(3.15)

– частота власних коливань ДГК, а і – сталі інтегрування, які визначаються початковими умовами. Наприклад, якщо початкова швидкість ( ) дорівнює нулю, а початкове положення головної осі ДГК відхилене на кут від площини меридіану, то (3.14) набуває вигляду

.

Якщо по вимірювальній осі ДГК діє момент в’язкого тертя , то власні коливання ДГК стають загасаючими і визначаються виразом

,

де .

За наявності постійного моменту сил ( ) вздовж вимірювальної осі ДГК його положення рівноваги дещо зміщується від площини меридіану на кут:

(3.16)

3.1.2.2. Рух дгк при кутовій вібрації

Рівняння руху (3.9) ДГК за умови відсутності моментів сил вздовж вимірювальної осі можна подати у формі

, (3.17)

де не враховується рух основи навколо вимірювальної осі. Якщо припустити, що основа не переміщується по поверхні Землі ( ), проекції і матимуть вигляд (див. рис. 3.1):

;

. (3.18)

Припустимо, що північна ( ) і східна ( ) складові відносної кутової швидкості основи змінюються за гармонічним законом з частотою :

; . (3.19)

Покладемо кут відхилення від меридіана малим ( ) і будемо розв’язувати задачу методом послідовних наближень. Вважаючи всі кутові швидкості малими, утворимо рівняння першого наближення зі членів не вище першого порядку мализни:

, (3.20)

а у рівнянні другого наближення удержимо члени до другого порядку мализни, причому величину кута , що входить у члени другого порядку, замінимо на розв’язок рівняння (1.20):

.

Після перетворень і відкидання величин більше другого порядку мализни одержимо

. (3.21)

Розв’язуючи спочатку рівняння (3.20) у формі

,

а далі підставляючи цей розв’язок у праву частину рівняння (3.21) і розв’язуючи його, можна дійти уточненого розв’язку другого наближення.

Частковий розв’язок неоднорідного рівняння (3.20) із врахуванням (3.19) має вигляд:

, (3.22)

де використане позначення

, (3.23)

відношення частоти коливань основи до частоти власних коливань гірокомпаса.

У кінцевому підсумку нас буде цікавити не повний розв’язок рівнянь другого наближення, а лише його стала складова за період вібрації (хитавиці), тому що саме вона визначає сталу складову зміщення положення рівноваги гірокомпаса від меридіана:

.

Застосуємо операцію усереднення до обох частин рівняння (3.21). Одержуємо

.

Постійна складова відхилення положення рівноваги гірокомпаса від меридіана має вигляд:

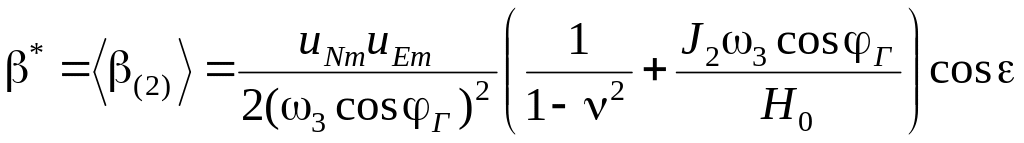. (3.24)

З отриманої формули випливає, що практично завжди у виразі сталої складової (3.22) можна нехтувати другим доданком у дужках правої частини, тому вібраційну похибку двоступеневого гірокомпаса можна оцінювати за формулою:

. (3.25)

Через те, що частота власних коливань двоступеневого гірокомпасу є доволі малою величиною (нагадаємо, що період цих коливань складає величину порядку півхвилини), то майже усі реальні кутові коливання основи слід віднести до високочастотних, бо їхня частота набагато перевищує частоту коливань гірокомпасу ( ). З врахуванням цього формулу (3.25) можна замінити на таку наближену

. (3.26)

Тут величини і мають сенс амплітуд кутів хитавиці (вібрації) основи відповідно навколо осей "північ-південь" і "схід-захід".