Момент силы относительно точки и оси.

Как известно из практики, приложение силы к телу, закрепленному в одной точке, вызывает его поворот вокруг этой точки. Эффективность вращательного воздействия силы будет определяться моментом силы относительно данной точки - взятым со знаком плюс или минус произведением модуля силы на длину перпендикуляра, опущенного из этой точки на линию действия силы (плечо силы).

Момент силы будем считать положительным, если сила стремится повернуть тело против хода часовой стрелки, если по ходу часовой стрелки- отрицательным.

Момент силы имеет направление и, следовательно, является величиной векторной. Моментом силы F относительно точки О называется приложенный в центре О вектор , модуль которого равен произведению модуля силы на плечо и который направлен перпендикулярно плоскости, проходящей через центр О и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки.

Если линия действия силы проходит через центр момента, то плечо, а, следовательно, и момент силы относительно этой точки будут равна нулю. Обозначается момент (H*м).

Кроме рассмотренного понятия, важную роль играет и понятие момента силы относительно оси.

Разложим силу F на две составляющие: одна N - параллельна оси Z, вторая Q - лежит в плоскости перпендикулярной оси Z. Очевидно, что составляющая N будет пытаться сдвинуть плоскость вдоль оси Z, не поворачивая её. Составляющая Q вызывает вращательный эффект, равный моменту силы Q относительно точки О. Отсюда приходим к заключению, что момент силы F относительно оси Z равен моменту силы Q относительно точки на оси Z.

Или: Момент силы F относительно оси Z равен алгебраическому моменту проекций этой силы на плоскость, перпендикулярную оси Z , взятому относительно точки пересечения оси с этой плоскостью.

Момент положительный, если с положительного конца оси поворот от силы виден против часовой стрелки, а отрицательный, если по часовой стрелке. Возможны частные случаи:

1.Если сила параллельна оси, момент равен нулю.

2.Если сила пересекает ось, момент равен нулю.

3.Если сила перпендикулярна оси, то её момент максимален.

Момент пары сил.

Парой сил называется система двух равных по модулю и противоположно направленных, параллельных сил. Пара сил не имеет равнодействующей: её нельзя заменить одной эквивалентной силой. d - плечо пары сил (перпендикуляр). Момент пары сил- произведение модуля одной из сил на плечо этой пары: , вектор которого m, направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки . Но в отличии от момента силы, момент пары может быть приложен в любой точке: .

по ,

а получим

или в векторной форме

.

Рассмотрим основные свойства пар, устанавливающие условия эквивалентности двух пар.

1 . Две пары лежащие в плоскости и имеющие численно равные моменты и одинаковое направление вращения, эквивалентны.(рис.6) В точках А и В приложена пара сил F иF'. Через эти точки проведём две параллельные линии АС и ВД и разложим силы F F' на эти линии и на АВ. Поскольку параллелограммы подобны и их диагонали равны, то иQ= -Q' (эти силы уравновесятся) иP= -P'.

ЗаменаF иF' новой системой сил привела к тому, что момент(F,F') был заменен моментом пары(P,P'). Поскольку точки Д и С, а также направления линий АС и ВД выбирались произвольно, то новая пара может оказаться в плоскости где угодно.

Из условия эквивалентности получается ряд важных следствий:

1)Данную пару сил, не изменяя её действия на тело можно как угодно переносить в её плоскости. Действие пары не зависит от её положения в плоскости.

2) Не изменяя действия данной пары на тело, можно изменять модуль силы и плечо этой пары, но при условии, чтобы её момент и направление оставались неизменными.

2. Две данные пары всегда можно привести к одному плечу.

3. Данную пару, не изменяя её действия на тело, можно переносить в любую плоскость, параллельную плоскости этой пары.

Таким образом, две пары сил, имеющих одинаковые моменты, эквивалентны друг другу. Они могут быть преобразованы одна в другую.

Сложение пар сил.

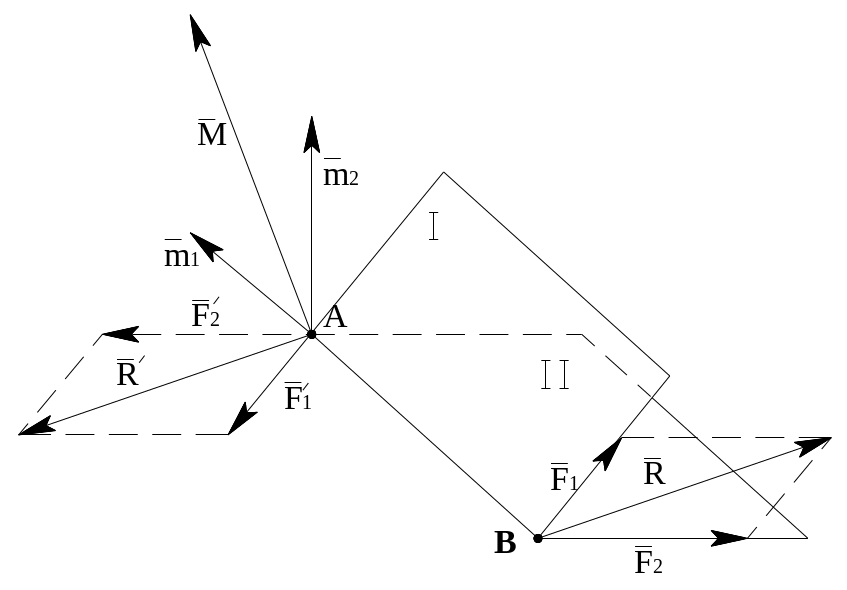Теорема: Система пар сил, действующая на тело, эквивалентна одной паре с моментом, равным геометрической сумме моментов слагаемых пар. Рассмотрим две пары и , лежащие в плоскостях I и II соответственно. Представим их в виде пар сил F₁; F₁' и F₂;F₂', приложенных в точках A и B на расстоянии d на линии пересечения плоскостей ( ). Сложив силы в точках А и В получаем R₁ и R₂ c моментом пары М. Поскольку , то . Если на тело действует несколько пар, то . Условие равновесия тела под действием пар сил: .

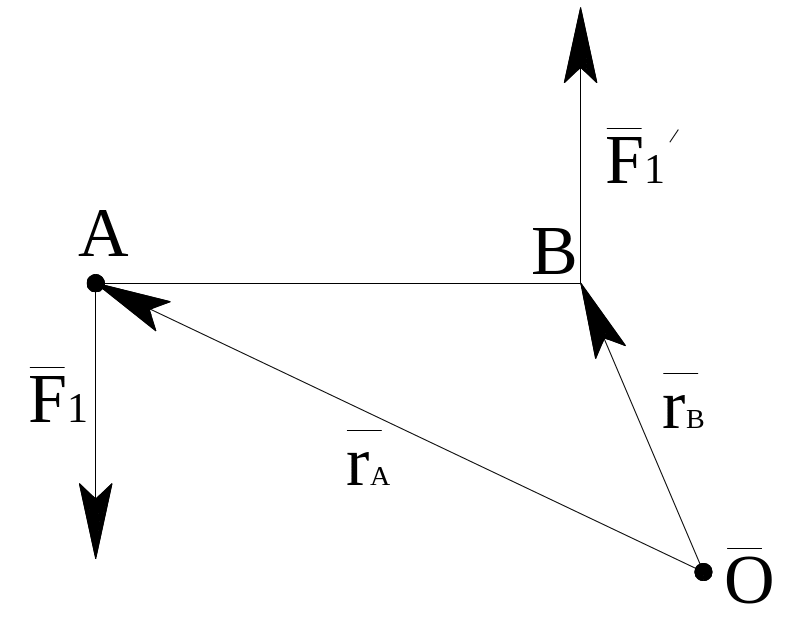
Параллельный перенос силы.

Теорема: Силу, приложенную к телу можно не изменяя оказываемого ею действия, переносить из данной точки в любую другую точку тела, прибавляя к нему пару сил с моментом, равным моменту переносимой силы относительно точки переноса. Пусть действует в точке А. Приложим в т. В две уравновешивающиеся силы , равные по модулю. Но две силы представляют собой пару сил с моментом , а равна , но приложена в т.В. Таким образом рассматриваемая система эквивалентна первоначальной.

Приведение системы сил к заданному центру.

Приведение системы сил к центру выполняется с целью упрощения расчетной схемы, которая в результате приведения будет состоять из одной результирующей силы и одной пары сил.

На основе теоремы о параллельном переносе, перенесем точки приложения всех приложенных к телу сил в т.О. Сложив векторы сходящихся сил в т. О по правилу параллелограмма, получим результирующий вектор силы .

Однако, при переносе сил, были получены моменты ; ; . Сложив векторы моментов этих пар, получим .

- главный вектор системы сил,

- главный момент системы сил относительно центра О

Фермы.

Ферма - конструкция, состоящая из стержней, соединенных между собой по концам шарнирами и образующих геометрически неизменяемую систему (мосты, подъёмные краны, опорные конструкции и т.д.).

Узел -шарнирное соединение стержней фермы.

Зависимость между числом стержней m и числом узлов n фермы без лишних стержней (при исключении которых ферма не теряет геометрической неизменяемости).

m = 2n-3,

где 3 - число узлов основного треугольника. Если m<2n-3, число стержней недостаточно для неизменяемости – это механизм. Если m>2n-3, - то ферма с лишними стержнями статически неопределима.

Основные допущения при расчётах ферм:

1. Все стержни прямолинейные.

2. Трение в шарнирах отсутствует.

3. Все нагрузки лежат в плоскости фермы и приложены в её узлах.

4. Собственным весом стержней фермы пренебрегаем.

При этих условиях, стержни, испытывают только сжатие или растяжение.

Для расчета усилий в стержнях существует несколько способов:

1 . Способ вырезания узлов - последовательное рассмотрение равновесия сил, сходящихся в каждом из узлов (реакции стержней и связей). Составляется система уравнений равновесия (или замкнутый силовой многоугольник). Решение задачи всегда начинают с определения опорных реакций - ферма

с читается твердым телом.  R_А и R_В.

Вырезаем узел, в котором сходятся два стержня - т. А.

Силы N₁ и N₂ направляем произвольно, составляем уравнения равновесия для него: , и находим N₁ и N₂. Затем вырезаем следующий узел, и т.д.

Графически решение еще более простое: Масштабный коэффициент  = N/l, .где: l – длина вектора N на плане сил. Для определения направления сил необходимо обойти многоугольники в направлении известной силы. Характер нагрузки в стержне оценивается направлением силы: если реакция данного стержня, приложенного к вырезанному узлу, направлена к этому узлу, то стержень сжат, если эта реакция направлена от узла - стержень растянут.

1. Способ Риттера (способ разрезов фермы)- аналитический способ. Как и в предыдущем случае (рис.1), сначала определяются опорные реакции. Для определения усилий в стержнях разрежем ферму на две части так, чтобы рассеченными оказались не более трех стержней (но не узлы). Рассматривая равновесие отсеченной части, находим усилия в стержнях.

, ,  N₄, N₅, N₆.

Характер силы в стержне определяется аналогично предыдущему способу: к узлу - сжатие, от узла - растяжение. Сила получена с минусом - значит направление, выбранное произвольно, необходимо изменить на обратное. Делая ряд последовательных разрезов фермы по различным стержням, определяют остальные усилия.

Пространственная система сил.

Метод приведения плоской системы сил к произвольно выбранному центру, применим к любой системе. Следовательно: Систему сил, линии действия которых как угодно расположены в пространстве, можно привести в общем случае к одной силе, приложенной в произвольно выбранной точке тела и паре сил.

,

Эти векторные суммы называются главным вектором системы сил и главным моментом системы соответственно.

Аналитические формулы, определяющие модули и направления главного вектора и главного момента сил имеют вид:

, , ,

Н аправляющие косинусы: , , .

Для моментов относительно координатных осей, в соответствии с теоремой Вариньона, имеем: . Но оси х следовательно , тогда .

Окончательно запишем:

, , .

Это проекции вектора на координатные оси.

Модуль вектора момента найдем по формуле:

,

направляющие косинусы: , ,

Приведение пространственной системы сил к простейшему виду.

Система приводится к главному вектору и главному моменту.

1. , - система приводится к паре, с моментом, не зависящим от выбора центра О.

2. , - приводится к равнодействующей, линия действия которой, проходит через центр О.

3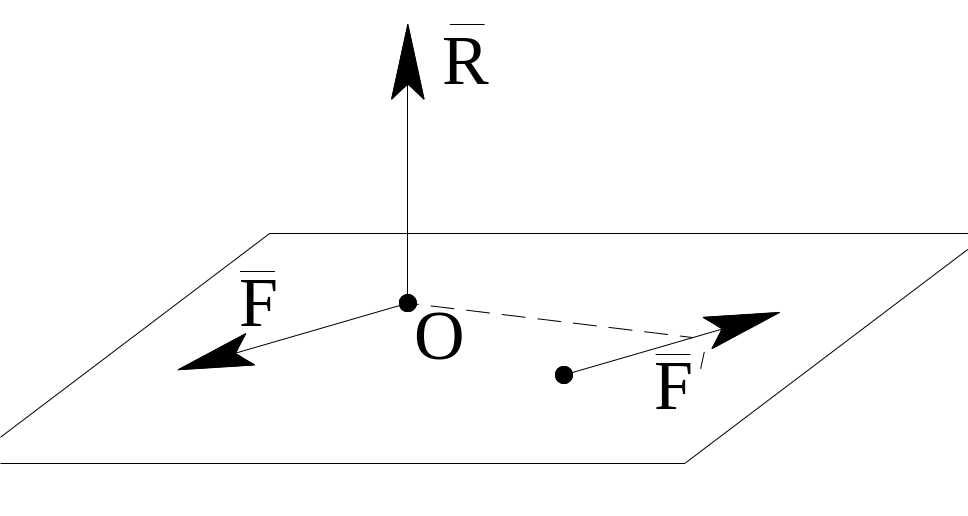 . Если , , но , то система приводится к равнодействующей, не проходящей через центр О.

4. , , но  - такая совокупность называется динамическим винтом, с прямой, по которой направлен - осью винта. Она проходит через точку О. (Дальнейшее упрощение невозможно!) .

5. , - общий случай. Приводится к динамическому винту, но ось не будет проходить через центр О.

Равновесие пространственной системы сил.

Необходимое и достаточное условие равновесия: , . Это имеет место когда:

, , , , , .

Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю.

Частные случаи:

1. Системы сходящихся сил. Все силы сходятся в одной точке. Примем её за начало координат: так как все силы пересекают координатные оси, то последние три условия удовлетворяются тождественно. Достаточно: , .

2. Система параллельных сил. Действуют параллельные сил, не лежащие в одной плоскости. Направим одну из координатных осей параллельно силам, тогда остаются три условия : , , .

Равновесие несвободного твердого тела.

1 . Тело с одной неподвижной точкой (с тремя степенями свободы). При равновесии твердого тела с одной неподвижной точкой сумма моментов всех действующих на тело заданных сил относительно каждой из трех координатных осей, начало которых находится в неподвижной точке, равна нулю (равнодействующая проходит через точку О ).

, , , , , .

2. Тело с двумя неподвижными точками (с одной степенью свободы). Считая, что результирующая проходит через точку О:

, , .

О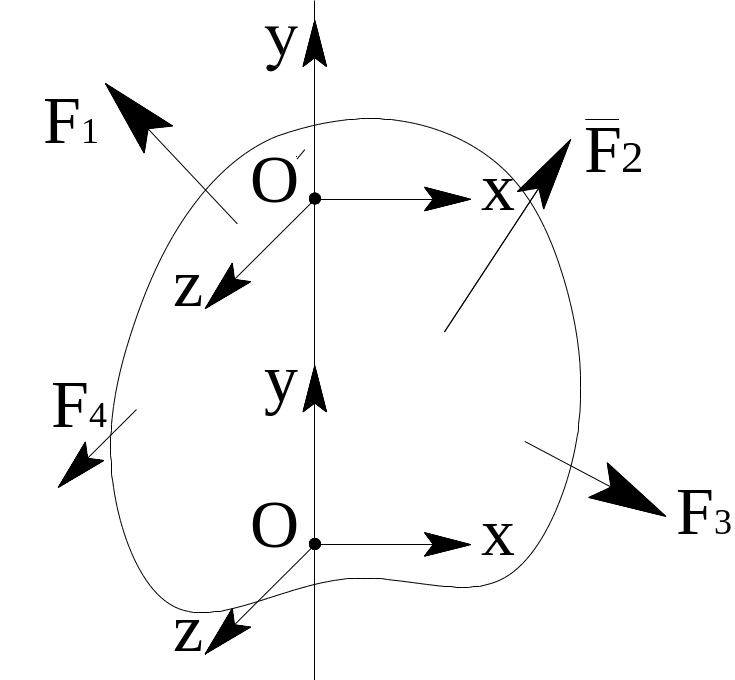 кончательно:

, , ,

, , .

П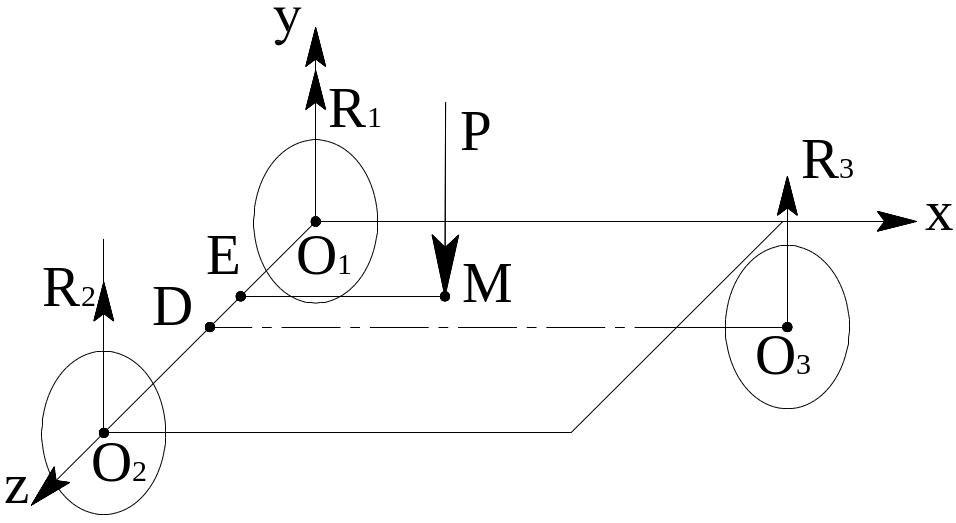 ри равновесии твердого тела с двумя неподвижными точками ( с неподвижной осью) сумма моментов всех действующих на него заданных сил относительно неподвижной оси равно нулю. Задача статически неопределимая: можно определить только суммарную силу вдоль оси .

Рассмотрим пример пространственной системы сил. Вес груза равен Р = 1000 Н О₁О₂ = 1 м, О₃ Д = 1.6 м, О₁Е = 0.4 м, ЕН = 0.6 м.,

R₁, R₂, R ₃ - ?

Составим систему уравнений равновесия:

,

,

где: ; ;

; ,

.

Отсюда получим:

, окончательно: Н

, -- Н

, -- Н

Центр тяжести.

Ц ентр тяжести системы параллельных сил. Наиболее характерная задача: исследование объектов под действием гравитационных сил.

Равнодействующая системы равна ,представляет собой вес тела и проходит через т. С - центр тяжести системы.

Координаты центра параллельных сил т. С можно найти на основе теоремы Вариньона:

, то есть ; то же относительно других осей. Окончательно:

; ; .

Центр тяжести – геометрическая точка, которая может лежать вне пределов тела.

Координаты центров тяжести однородных тел.

Вес тела , где V – объем тела,  - удельный вес. То же для любой его части. Подставив эти произведения в полученные выше выражения и сократив на , получим: ; ; . Координаты ЦТ от плотности вещества не зависят – это ЦТ объема тела.

Если тело представляет собой тонкую однородную пластину, то:

; ,

где: S - площадь пластины.

Полученные координаты - положение центра тяжести площади.

Если тело - материальная линия (проволока):

; ; .

где: L - длина линии; l_i - длина частей.

Положение центра тяжести симметричного тела.

1. Если точки приложения всех данных параллельных сил лежат в одной и той же плоскости, или на одной и той же прямой, то центр этой системы параллельных сил лежит соответственно в той же плоскости или на той же прямой. ( , но все x_i=0, следовательно, x_c=0).

2. Если однородное тело имеет плоскость, или ось симметрии, то центр тяжести такого тела лежит соответственно в этой плоскости, на этой оси или в этом центре симметрии. (При наличии плоскости симметрии, все тело можно разбить на симметричные элементарные частицы. Поскольку веса этих частиц будут одинаковы, то их результирующие всегда будут лежать в плоскости симметрии, следовательно, и центр тяжести лежит в этой плоскости).