Методы сжатия без потерь

Практически все методы сжатия без потерь основаны на одной из двух довольно простых идей.

Одна из них впервые появилась в методе сжатия текстовой информации, предложенном в 1952 году Хафманом. Вы знаете, что стандартно каждый символ текста кодируется одним байтом. Но дело в том, что одни буквы встречаются чаще, а другие реже. Например, в тексте, написанном на русском языке, в каждой тысяче символов в среднем будет 90 букв "о", 72 – "е" и только 2 – "ф". Больше же всего окажется пробелов: сто семьдесят четыре. Если для наиболее распространенных символов использовать более короткие коды (меньше 8 бит), а для менее распространенных – длинные (больше 8 бит), текст в целом займет меньше памяти, чем при стандартной кодировке.

Другие методы основаны на том, что если некоторая последовательность байт встречается в файле многократно, ее можно записать один раз в особую таблицу, а потом просто указывать: "взять столько-то байт из такого-то места таблицы".

Код Шеннона-Фано (статистическое кодирование)

Кодирование Шеннона-Фано является одним из самых первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон (Shannon) и Фано (Fano). Данный метод сжатия имеет большое сходство с кодированием Хаффмана, которое появилось на несколько лет позже. Главная идея этого метода - заменить часто встречающиеся символы более короткими кодами, а редко встречающиеся последовательности более длинными кодами. Таким образом, алгоритм основывается на кодах переменной длины. Для того, чтобы декомпрессор впоследствии смог раскодировать сжатую последовательность, коды Шеннона-Фано должны обладать уникальностью, то есть, несмотря на их переменную длину, каждый код уникально определяет один закодированный символ и не является префиксом любого другого кода.

Рассмотрим алгоритм вычисления кодов Шеннона-Фано (для наглядности возьмём в качестве примера последовательность 'aa bbb cccc ddddd'). Для вычисления кодов, необходимо создать таблицу уникальных символов сообщения c_i и их вероятностей p(c_i), и отсортировать её в порядке убывания вероятности символов.

ci	p(ci)
d	5 / 17
c	4 / 17
space	3 / 17
b	3 / 17
a	2 / 17

Далее, таблица символов делится на две группы таким образом, чтобы каждая из групп имела приблизительно одинаковую частоту по сумме символов. Первой группе устанавливается начало кода в '0', второй в '1'. Для вычисления следующих бит кодов символов, данная процедура повторяется рекурсивно для каждой группы, в которой больше одного символа. Таким образом, для нашего случая получаем следующие коды символов:

символ	код
d	00
c	01
space	10
b	110
a	111

Длина кода s_i в полученной таблице равна int(-lg p(c_i)), если символы удалость разделить на группы с одинаковой частотой, в противном случае, длина кода равна int(-lg p(c_i)) + 1.

int(-lg p(c_i)) <= s_i <= int(-lg p(c_i)) + 1

Используя полученную таблицу кодов, кодируем входной поток - заменяем каждый символ соответствующим кодом. Естественно для расжатия полученной последовательности, данную таблицу необходимо сохранять вместе со сжатым потоком, что является одним из недостатков данного метода. В сжатом виде, наша последовательность принимает вид:

111111101101101101001010101100000000000

длиной в 39 бит. Учитывая, что оригинал имел длину равную 136 бит, получаем коэффициент сжатия ~28% - не так уж и плохо.

Глядя на полученную последовательность, возникает вопрос: "А как же теперь это расжать ?". Мы не можем, как в случае кодирования, заменять каждые 8 бит входного потока кодом переменной длины. При расжатии нам необходимо всё сделать наоборот - заменить код переменной длины символом длиной 8 бит. В данном случае, лучше всего будет использовать бинарное дерево, листьями которого будут являться символы.

Процесс создания кода Код Шеннона — Фано можно представить с помощью дерева. Построение этого дерева начинается от корня. Всё множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмана.

Пример кодового дерева

Исходные символы:

A (частота встречаемости 50)

B (частота встречаемости 39)

C (частота встречаемости 18)

D (частота встречаемости 49)

E (частота встречаемости 35)

F (частота встречаемости 24)

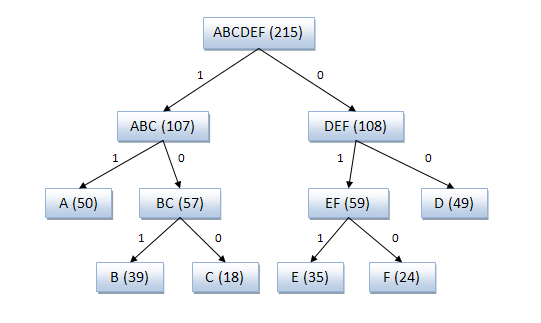
Полученный код: A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.

Кодирование Шеннона – Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев, длина последовательности, сжатой по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях могут сформироваться неоптимальные коды Шеннона – Фано, поэтому более эффективным считается сжатие методом Хаффмана.

Но и код Шеннона – Фано, и код Хаффмана имеют один существенный недостаток - они никак не учитывают взаимосвязей между символами, которые присутствуют практически в любом тексте. Например, если в тексте на английском языке нам встречается буква q, то мы с уверенностью сможем сказать, что после нее будет идти буква u.

Примеров взаимных связей, или, говоря техническим языком, корреляций, можно привести множество. Для кодирования данных с корреляционными зависимостями предназначен код LZW.