Регулярность отчетов с.130

Равномерная дискретизация

В результате дискретизации сигнал заменяется дискретными отсчетными значениями, взятыми через определенные моменты времени. Очень важен правильный выбор интервала времени.

а) По частотному критерию. с.135

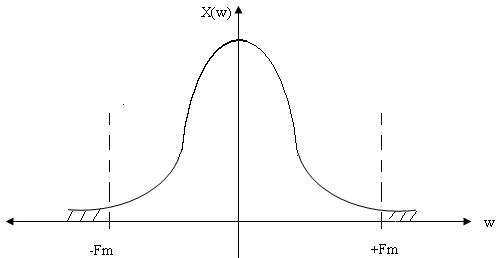
Задача о выборе интервала дискретизации наиболее просо решается для сигнала с ограниченным спектром на основании теоремы Котельникова, или теоремы отсчетов.

Теорема

Если наивысшая частота в спектре ограничена частотой , то функция x(t) полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более чем на секунд.

Другими словами исходная непрерывная функция x(t) может быть полностью восстановлена по ее отсчетам при скорости дискретизации .

Физическая основа теоремы выявляется при рассмотрении связи между формой функции и шириной ее спектра только в том случае, когда спектр функции безграничен, ее значения в сколь угодно близкие моменты времени могут изменяться произвольно, то есть между ними отсутствует корреляционная связь. Сокращение высокочастотной части спектра до граничной частоты равнозначно устранению из временной функции выбросов, которые могли быть сформированы этими высокочастотными составляющими. При меньших граничных частотах и имеет более сглаженные функции времени.

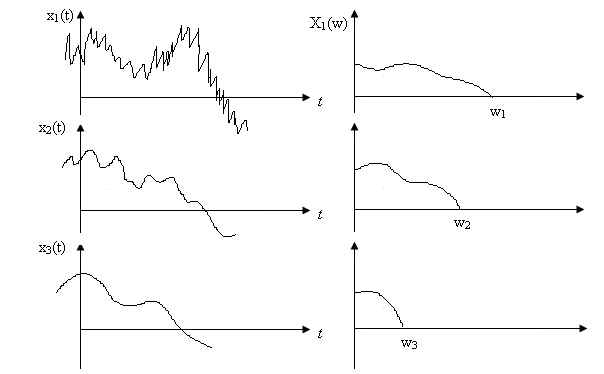
Функция x(t), допускающая преобразование функции и имеющая неограниченный спектр, ограниченный полюсами частот от 0 до , полностью определяется дискретным рядом своих мгновенных значений, отсчитанных через интервалы времени

.

верхняя, граничная частота.

Теорему Котельникова можно применить также к функциям, частотный спектр которых не начинается от 0, а занимает полосу частот . В этом случае .

Пример:

Теорема Котельникова относится к сигналам с ограниченным спектром, но ограниченному (финитному) спектру соответствует сигнал бесконечной длительности. Реальные сигналы имеют конечную длительность, и, следовательно, их спектр безграничен. Для практических целей необходимо восстановление сигнала с заданной точностью, поэтому теорему Котельникова можно рассматривать как приближенную для функций с ограниченным спектром. Однако практически всегда можно так определить верхнюю частоту Fm, чтобы «хвосты» функции времени, обусловленные отсеканием частот, содержали бы малую долю энергии по сравнению с энергией самого сигнала x(t). Ограничение спектра финитного сигнала (имеющего бесконечный спектр) приводит к СКП дискретизации.

В действительности величина СКП в силу многих причин больше величины, определяемой данным выражением.

Для принятых допущений для сигнала длительностью Тс общее число независимых значений x(nT), которое необходимо для полного задания сигнала, будет равно

Число N называют числом степеней свободы сигнала x(t) или базой сигнала.

Поскольку все реально существующие непрерывные сигналы связи представляют собой случайные процессы с бесконечно широким спектром, причем основная энергия сосредоточена в относительно узкой полосе частот, перед дискретизацией необходимо с помощью фильтра нижних частот ограничить спектр сигнала некоторой частотой F_В. Для телефонных сигналов необходимо использовать ФНЧ с частотой среза F_В=3,4 кГц. Частота дискретизации для телефонных сигналов выбрана равной 8 кГц.

Характер возникающих искажений во временной области при нарушении условия (7.2.5) можно наглядно видеть на рис. 7.2.5. На рисунке показаны три возможных варианта соотношения частот гармонических сигналов с постоянной частотой их дискретизации.

 График А – частота гармонического сигнала меньше частоты Найквиста. Дискретным отсчетам может соответствовать только исходная гармоника, амплитуда, частота и фаза которой могут быть однозначно определены по любым трем последовательным точкам (три уравнения, три неизвестных).

 График В – частота гармонического сигнала равна частоте Найквиста. Это означает периодическое повторение каждой пары последовательных отсчетов, а, следовательно, для решения имеется только два уравнения с тремя неизвестными с возможностью определения только частоты, и то при условии, что начальная фаза сигнала не совпадает с начальной фазой частоты дискретизации (в этом случае все отсчеты нулевые). Амплитуда и фаза сигнала определяются однозначно только при условии совпадения отсчетов с экстремумами гармоники.

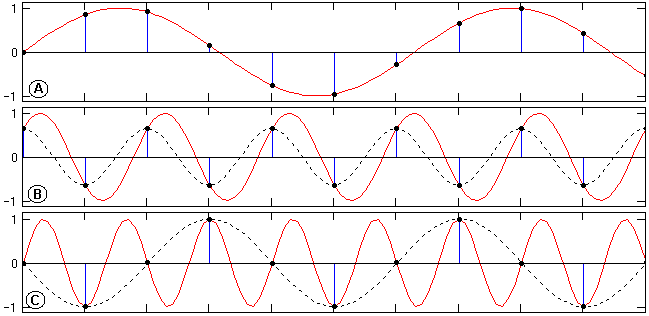
Рис. 7.2.5. Дискретизация гармоник с разной частотой.

 График С – частота гармонического сигнала больше частоты Найквиста. Решение трех уравнений по трем последовательным точкам позволяет определить амплитуду гармоники, но дает искаженные значения частоты и фазы колебания (показано пунктиром). Это так называемый эффект появления ложных (кажущихся) частот (aliasing). Частоты гармонических колебаний выше частоты Найквиста как бы зеркально "отражаются" в главный частотный диапазон от его границ (на частоте Найквиста), что можно видеть на рис. 7.2.4 для действительного спектра сигнала S₁(), показанного точками. Этот эффект аналогичен всем известному эффекту обратного вращения колес автомобиля (и любых других быстро вращающихся объектов) на экранах кино и телевизоров, когда скорость их вращения начинает превышать частоту смены кадров.

б) По критерию наибольшего отклонения

В процессе дискретизации непрерывная функция x(t), имеющая (n+1) ограниченных производных, аппроксимируется многочленом n-ой степени. В зависимости от выбранного способа восстановления он может быть интерполирующим или экстраполирующим.

Интерполирование – точное или приближенное восстановление функции определенного класса на заданном интервале по известным ее значениям, и, может быть по значениям ее производных в конечном множестве точек, принадлежащих этому интервалу.

Экстраполирование – распространение результатов, полученных из наблюдений над одной частью явления, на другую ее часть, то есть если известны значения функции на отрезке [a, b], то экстраполированием можно определить значения функции в точках, лежащих вне этого отрезка.

Для обработки сигналов более эффективны интерполяционные методы приближения (аппроксимации), обеспечивающие меньшую избыточность отсчетов по сравнению с экстраполяционными методами. Однако использование ИМ связано с задержкой сигнала на интервал интерполяции.

Экстраполяционные методы (ЭМ) не требуют задержки сигнала при проведении дискретизации. Еще, они могут использоваться в управляющих системах, работающих в реальном времени.

Погрешность восстановления функции x(t) многочленом v(t) на каждом участке аппроксимации определяются остаточным членом

Задача обеспечения минимальной погрешности при восстановлении сигнала на практике не ставится. Обычно указывается ее допустимое значение .

Следовательно, шаг дискретизации должен быть выбран из условия

.