Упорядочение Уолша-Пэли

Рассмотрим в качестве примера функции Уолша, упорядоченные по Пэли.

Она образуется таким образом, что каждая функция Уолша с номером α представлена произведением функций R с номерами, совпадающими с номерами разрядов двоичного представления α, содержащих 1.

Построим систему Пэли, для N=8 и :

W₀(θ) = R₀(θ)

W₁(θ) = W₀₀₁(θ) = R₁(θ)

W₂(θ) = W₀₁₀(θ) = R₂(θ)

W₃(θ) = W₀₁₁(θ) = R₁(θ) R₂(θ)

W₄(θ) = W₁₀₀(θ) = R₃(θ)

W₅(θ) = W₁₀₁(θ) = R₁(θ) R₃(θ)

W₆(θ) = W₁₁₀(θ) = R₂(θ) R₃(θ)

W₇(θ) = W₁₁₁(θ) = R₁(θ) R₂(θ) R₃(θ)

Это диадическое упорядочение.

Упорядочение Адамара

Систему Адамара можно получить из системы Пэли двоичной инверсией номеров функций, то есть записью разрядов и двоичного представления номера функции Уолша в обратном порядке. То есть, при N=8 третья функция в системе Адамара (α=3=011) совпадает с шестой функцией в системе Пэли (α=3=011). Поучила широкое распространение.

Это естественное упорядочение.

Упорядочение Уолша-Уолша

Функции Уолша, упорядоченные по Уолшу, представляют собой систему, в которой четные функции чередуются с нечетными. В этом смысле, она подобна тригонометрической системе, и ее иногда по аналогии обозначают как .

При этом

Все функции упорядочены по числу пересечений нулевого уровня. Это упорядочение по частоте.

Функции Уолша, упорядоченные по Уолшу (упорядочение по частости или по системе Хармута) располагаются в порядке увеличения числа знакоперемен на интервале определения.

Эту систему также можно получить из системы Пэли. При этом номер соответствующей функции Уолша-Пэли равен коду Грея двоичного разложения заданного номера функции Уолша-Уолша.

Пример:

Пусть в разложении Уолша-Пэли N=16. Тогда восьмая функция в разложении Уолша-Уолша будет двенадцатая в разложении Уолша – Пэли, так как

1000 -8

+ 100

1100 -12 Код Грея

или четвертая будет шестая:

0100 -4

+ 0010

0110 -6 Код Грея и так далее.

Система Уолша-Уолша представляет собой систему, в которой четные функции (относительно середины интервала, то есть 0,5) чередуются с нечетными. В этом смысле она подобна тригонометрической системе и ее иногда по аналогии обозначают как

При этом

где m – частость.

Как мы видим, все системы взаимосвязаны друг с другом. Поэтому их можно построить, используя одну систему (например, Пэли) в качестве базовой.

Вывод. Так как все рассмотренные системы используют одни и те же функции Уолша, но в различной последовательности, то с общей точки зрения для представления сигналов они равноправны. Различие этих систем может проявляться при формировании отдельных свойств разложения конкретных сигналов. Так, например, для широкого класса непрерывных сигналов спектр по функциям Уолша-Пэли сходится быстрее, чем по функциям других систем, то есть коэффициенты разложения сигналов по функциям Уолша-Пэли с возрастанием их номеров убывают по абсолютному значению.

Цифровое представление аналоговых сигналов

Сообщения могут быть функциями времени (когда информация представлена в виде первичных сигналов: речь, музыка) и не является ими (когда информация представлена в виде совокупности знаков).

Сигнал всегда является функцией времени. В зависимости от того, какие значения могут принимать аргумент (время t) и уровни сигналов их делят на 4 типа.

1. Непрерывный или аналоговый сигналы (случайные сигналы этого типа называются непрерывными случайными процессами). Они определены для всех моментов времени и могут принимать все значения из заданного диапазона. Чаще всего физические процессы, порождающие сигналы являются непрерывными. Этим и объясняется второе название сигналов данного типа аналоговый т.е. аналогичные порождающим процессам.

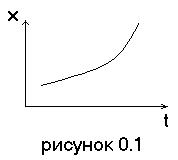
2. Дискретизированный или дискретно непрерывные сигналы (случайные сигналы этого типа называют процессами с дискретным временем или непрерывными случайными последовательностями). Они определены лишь в отдельные моменты времени и могут принимать любые значения уровня. Временной интервал Dt между соседними отсчетами называется шагом дискретизации. Часто такие сигналы называют дискретными по времени.

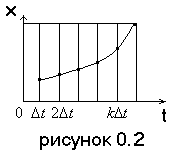
3. Дискретные по уровню или квантованные сигналы (случайные сигналы этого типа называют дискретными случайными процессами). Они определены для всех моментов времени и принимают лишь разрешенные значения уровней отделенные от друг друга на величину шага квантования Dx=xk+1+xk

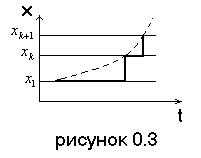
4. Дискретные по уровню и по времени сигналы (случайные сигналы этого типа называют дискретными случайными последовательностями). Они определены лишь в отдельные разрешенные моменты времени и могут принимать лишь разрешенные значения уровней.