Двоично – ортогональные сбф

Под этим названием объединяются СБФ меандрового типа Радемахера, Уолша и Хаара.

Эти системы принимают только значение ± (функции Радемахера и Уолша) либо ±1 и 0 (функция Хаара). Все эти системы взаимосвязаны между собой и каждую из них можно получить из другой, образуя соответствующую линейную комбинацию.

Функции Радемахера

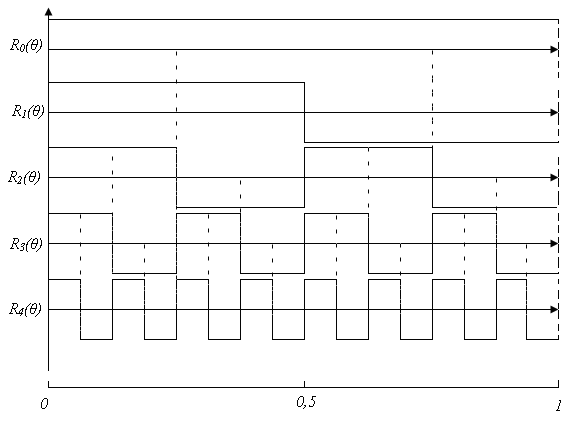
, где =t/T

Функции R ортогональны и нормированы, но не образуют полную систему, поскольку существуют и другие функции, ортогональные функции R, то есть . Для полных же систем нельзя подобрать ни одну функцию, которая была бы ортогональна одновременно ко всем функциям системы, так как функции R образуют неполный набор функций, это препятствует аппроксимации с их помощью четных функций x(t) (это и понятно, функции R – нечетны).

Функции Уолша (Walsh)

Этого недостатка лишен широко применяемый набор функций Уолша, являющийся полным.

На рассмотренном ниже графике представлены функций Уолша, упорядоченные по Пэли. Можно изменить их нумерацию и перестроить графики так, чтобы они были расположены в другом порядке, это иногда оказывается более целесообразным.

Любую интегрируемую на интервале функцию можно представить рядом Фурье по системе функций Уолша

с коэффициентами

Функции Уолша и Радемахера известны с 1922 года.

Функции Уолша, упорядоченные по Уолшу, при N=8 (или частости)

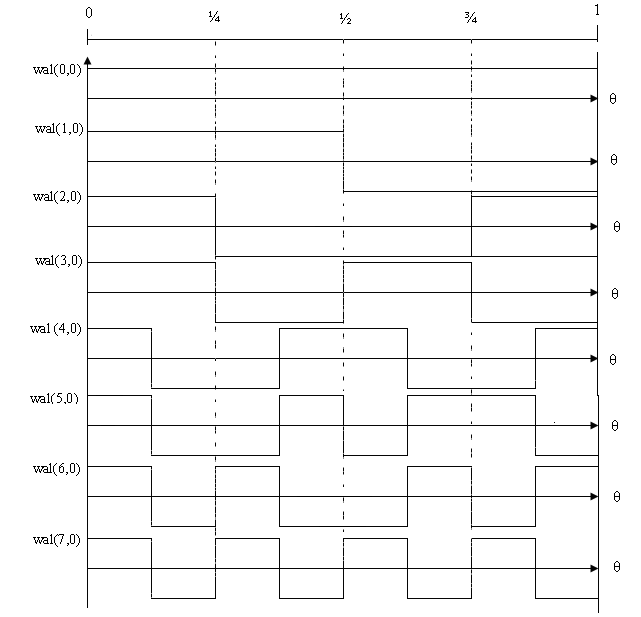
Частость – понятие, используемое для описания (различения) функций, точки пересечения нулевого уровня которых распределены неравномерно по интервалу, и которые не обязательно являются периодическими.

Частость функции равна половине числа пересечений нулевого уровня в секунду. Пусть η – число пересечений в открытом интервале (0, 1). Тогда частость S

Подобно тому, как частость измеряется числом периодов в секунду (герцах), частость определяется числом пересечений нулевого уровня в секунду.

Для нее можно использовать сокращение «zps» (zero – crossing per second)

s0 = 0 μ = 0 s1 = 1 μ = 1 s2 = 1 μ = 2 s3 = 2 μ = 3 s4 = 2 μ = 4 s5 = 3 μ = 5 s6 = 3 μ = 6 s7 = 4 μ = 7

wal (w, 0)	had (h, 0)	pal (p, 0)
0	0	0
1	4	1
2	6	3
3	2	2
4	3	6
5	7	7
6	5	5
7	1	4

Инверсия: запись в обратном порядке. Полуоткрытый интервал [0, N).

Системы Уолша образуются как дополнение системы Радемахера за счет функций, образованных всевозможными произведениями функций R. В зависимости от того, в какой последовательности были расположены эти функции, различают упорядочение по Уолшу (Walsh), Пэли (Paley), Адамару (Hadamar).