
- •Введение Архитектура систем передачи и распределения информации
- •Эталонная модель взаимодействия открытых систем (osi – Open System Interconnection)
- •Эталонная модель internet (tcp/ip)
- •Перечень сетевых протоколов
- •Протоколы
- •Способы установления соединений
- •Режимы передачи данных
- •Типы соединений
- •Сообщения и сигналы
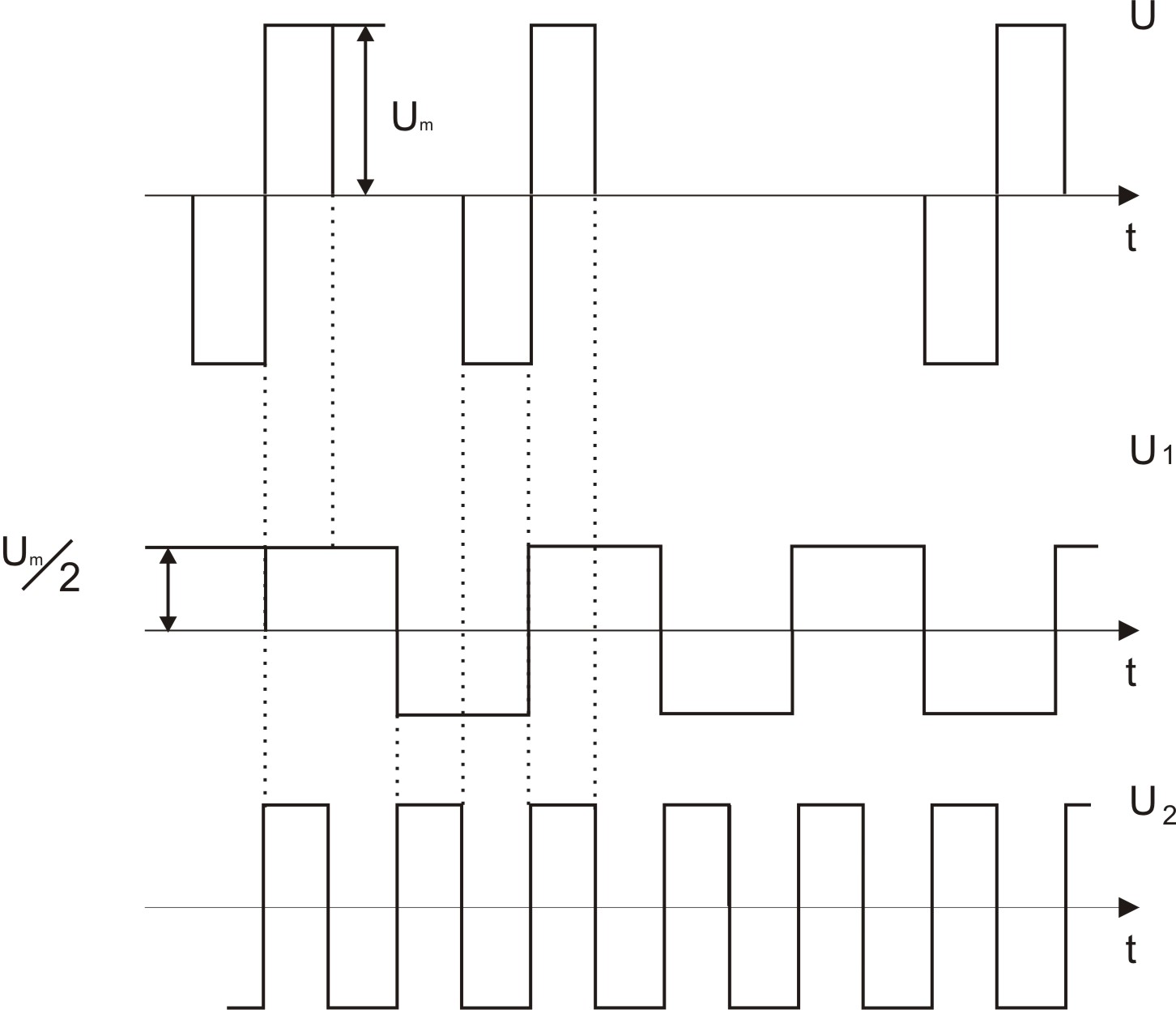
- •Модель стандартной одноканальная системы передачи информации
- •Аналоговые системы
- •Энтропия источника дискретных сообщений
- •Энтропия источника независимых сообщений
- •Энтропия источника зависимых сообщений
- •Избыточность источника сообщений
- •Математическая модель сообщения
- •Пропускная способность каналов
- •Дискретный канал без помех
- •Дискретный канал с помехами
- •Пропускная способность бинарного симметричного канала с помехами
- •Теоремы Шеннона для канала с шумами
- •Непрерывный канал с помехами
- •Теория сигналов Классификация сигналов
- •Геометрическое представление сигналов Множества сигналов
- •Пространство сигналов
- •Спектральное представление
- •Реальность спектра
- •Спектр дискретных сигналов
- •Системы единичных функций
- •Системы тригонометрических базисных функций
- •Двоично – ортогональные сбф
- •Упорядочение Уолша-Пэли
- •Упорядочение Адамара
- •Упорядочение Уолша-Уолша
- •Цифровое представление аналоговых сигналов
- •Общая постановка задачи дискретизации
- •Дискретизация сигналов Дискретные и цифровые сигналы
- •Спектры дискретизированных сигналов
- •Регулярность отчетов с.130
- •Восстановление сигналов
- •Квантование сигналов
- •Кодирование и декодирование сигналов
- •Аналого-цифровое преобразование Кодирование информации
- •М етоды сжатия информации
- •Методы сжатия без потерь
- •Код Шеннона-Фано (статистическое кодирование)
- •Блочное кодирование
- •Непомехоустойчивые коды
- •Принципы обнаружения и исправления ошибок
- •Переносчики информации
- •Преобразование сообщений в видеоимпульсный сигнал при передаче в основной полосе (видеоимпульсная передача)
- •Формирование линейного сигнала
- •Кодирование информации в локальных сетях
- •Аналоговая модуляция
- •Импульсная модуляция
- •Цифровая модуляция
- •Связь полосы пропускания со скоростью передачи (видеоимпульсов и радиоимпульсов)
- •Системы передачи с линейным разделением каналов Линейно-разделимые сигналы
- •Формирование канальных сигналов
- •Разделение по форме канальных сигналов
- •Временное разделение
- •Частотное разделение
- •Корреляционное разделение
- •Кодово – адресное разделение
- •Комбинированные методы линейного разделения
- •Нелинейное и комбинационное разделение каналов
- •Нелинейное разделение каналов Разделение сомножителей
- •Разделение по уровню
- •Комбинационные системы передачи
- •Обеспечение дальности связи
- •Общий принцип частотного уплотнения
Спектральное представление
Для повышения скорости выполнения операций по обработке информации в сочетании с высокой точностью и надежностью часто применяют переход от временного представления функций к их спектральному представлению.
Процессы в электрических цепях получаются тем сложнее, чем более сложной является форма сигналов. Иногда эта сложность затрудняет не только расчеты, но и понимание характера протекающих процессов. В этих случаях часто оказывается полезным использование понятие спектра сигнала.
Понятие спектра сигнала. Любой
сигнал может быть представлен в виде
суммы каких-либо сигналов другой формы,
которые являются составляющими заданного
сигнала. Например, последовательных
биполярных импульсов может быть
представлена как сумма двух составляющих
– прямоугольных колебаний
![]() и
и
![]()
Совокупность составляющих заданной формы, образующих в сумме некоторый сигнал, называют спектром этого сигнала, а составляющая сигнала – его спектральными составляющими.
Обобщенный ряд Фурье. В теории
и технике передачи аналоговых
сообщений широко используется разложение
непрерывных функций на интервале
определения
![]() в ряд
в ряд
![]() (1)
(1)
При этом система функций
![]() называется
базисной, а представление сигнала
в виде (1) – его разложением по системе
базисных функций или обобщенным
рядом. Если сигнал
называется
базисной, а представление сигнала
в виде (1) – его разложением по системе
базисных функций или обобщенным
рядом. Если сигнал
![]() является
комплексным, то и коэффициенты
является
комплексным, то и коэффициенты
![]() также
будут являться комплексными.
также
будут являться комплексными.
В общем случае ряд (1) для непрерывных
сигналов содержит бесконечное число
членов. Для практических расчетов такой
ряд обычно усекают до N-го
члена ряда, и имеет место аппроксимация
сигнала
конечным
рядом (1). Поэтому возникают задачи по
выбору системы функций
![]() позволяющих технически просто получить
набор коэффициентов
позволяющих технически просто получить
набор коэффициентов
![]() и минимизирующих погрешность
и минимизирующих погрешность
![]()
при заданном N по какому-либо определенному критерию. Обычно в качестве критерия приближения используют среднеквадратическую погрешность
![]() .
.
С этой точки зрения интерес представляют системы ортогональных функций Котельникова и Карунена-Лоева-Пугачёва (КЛП).
Для того, чтобы разложение сигнала в форме (1) было возможным, системы базисных функций (СБФ) должна удовлетворять ряду требований:
Быть упорядоченной системой линейно-независимых функций.
Быть полной для ортогональных функций, т.е. представлять в заданном базисе любой сигнал из заданного множества, любую реализацию случайного процесса
 удовлетворяющего условию
удовлетворяющего условию
 (условие
конечности энергии на интервале
определения
.
(условие
конечности энергии на интервале
определения
.Число линейно-независимых функций в полной система должна быть равно размерности рассматриваемого множества сигналов, т.е. количеству чисел, с помощью которых можно выбрать любой сигнал из этого множества. Когда рассматривается множество непрерывных сигналов произвольной формы, то их размерность бесконечно велика и в этом случае СБФ должна содержать также бесконечно большое число линейно независимых функций.
Наиболее удобно производить разложение
сигналов, если базисная система
![]() является
ортогональной на интервале определения
сигнала
:
является
ортогональной на интервале определения
сигнала
:
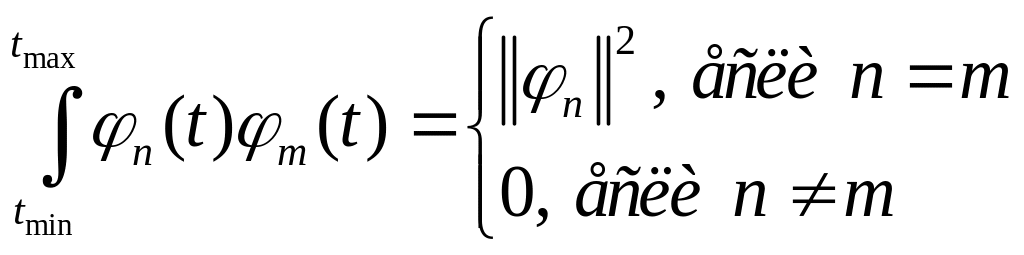
Величина
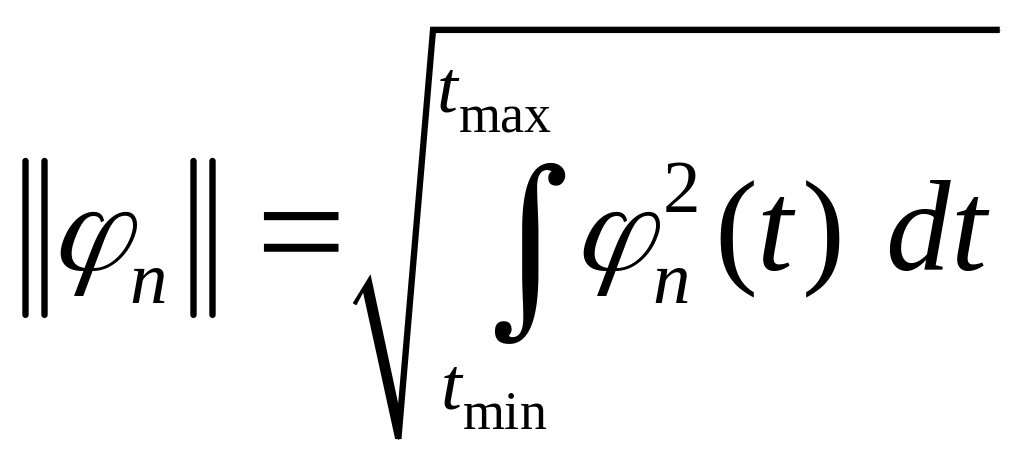
называется нормой функции
![]() .
.
Норма функции имеет геометрический и физический смысл:
геометрический – это длина вектора в пространстве сигналов
физический – квадрат нормы функции равен энергии сигналов.
Интервал определения ортогональных БФ называется также интервалом ортогональности.
Представление сигналов с помощью
ортогональных СБФ обладает тем важным
свойством, что повышение порядка
аппроксимируемого многочлена (![]() )
всегда улучшает аппроксимацию по
сравнению с представлением сигналов
неортогональных СБФ.
)
всегда улучшает аппроксимацию по
сравнению с представлением сигналов
неортогональных СБФ.
Система ортогональных функций называется также нормированной, если энергии всех базисных функций равны единице:
![]()
В этом случае СБФ называется ортонормированной. Любую систему линейно-независимых функций можно ортогонализировать и нормировать.
Примечание.
Если
-
случайный процесс, то
![]() -
случайные величины. В общем случае они
статистически зависимы, и эта связь
задается матрицей коэффициентов
корреляции
-
случайные величины. В общем случае они
статистически зависимы, и эта связь
задается матрицей коэффициентов
корреляции
![]() .
Математические ожидания коэффициентов
разложения
.
Математические ожидания коэффициентов
разложения
![]() равны нулю.
равны нулю.
Если выбраны также базисы функции, которые обеспечивают некоррелированность случайных величин , то разложение называют каноническим.
При представлении сигналов в форме (1)
необходимо решить вопрос о способе
вычисления спектральных коэффициентов.
Он во многом будет зависеть от принятого
критерия сходимости (приближения). Для
среднеквадратичного критерия коэффициенты
Сn выбирают
таким образом, чтобы СКП была минимальной.
Умножив обе части уравнения (1) на
![]() ,
проинтегрировав в пределах
,
проинтегрировав в пределах
![]() и учтя ортогональность функций
и учтя ортогональность функций
![]() и
и
![]() ,
получим важное соотношение
,
получим важное соотношение
 (2)
(2)
Ряд (1), в котором коэффициенты Сn
определены по данной формуле называются
обобщенным рядом Фурье по данной
системе
![]() .
Совокупность коэффициентов
.
Совокупность коэффициентов
![]() называется спектром
сигнала x(t)
в ортогональной системе
и полностью определяет этот сигнал.
называется спектром
сигнала x(t)
в ортогональной системе
и полностью определяет этот сигнал.
Ответьте на вопросы:
1) Что означает “вычислить спектр функции x(t)”?
2) В каких координатах строится спектр?
Итак, представление непрерывных функций
в форме (1) дает возможность представить
x(t)
в виде бесконечного, но счетного
массива чисел
![]() .
Кроме того, когда система
,
является полной, такое представление
возможно в виде конечного множества
чисел
.
Кроме того, когда система
,
является полной, такое представление
возможно в виде конечного множества
чисел
![]() :
:
![]()
Как мы уже знаем, ортогональная система называется полной, если увеличением числа членов в ряде среднеквадратическую ошибку
![]()
можно сделать сколь угодно малой.
Условие полноты можно записать в виде соотношения
![]()
Но
![]() ,
где Э – это энергия сигнала. Тогда
,
где Э – это энергия сигнала. Тогда
![]()
