Энтропия источника зависимых сообщений

В большинстве реальных случаев появление в последовательности элемента x_i зависит от того, какой элемент x_j был предшествующим.

Между различными состояниями системы существует статистическая связь, которая может быть связана графом вероятности перехода. Тогда взаимосвязь элементов сообщений или состояний системы характеризуется матрицей условных вероятностей:

Для зависимых элементов энтропия источника H(x) получается усреднением условной энтропии H(x|x_j) по вероятностям появления элементов.

Пример

Найти энтропию источника, описываемую графом вероятности перехода. Вероятности состояний P(x₁), P(x₂), P(x₃) равны.

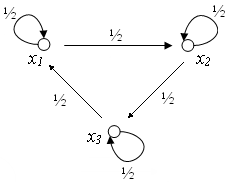
Решение

Нетрудно заметить, что

Тогда

Ответ: энтропия источника H(x)=1.

Избыточность источника сообщений

Если бы сообщения передавались бы с помощью равновероятных букв алфавита и между собой статистически независимых, то энтропия таких сообщений была бы максимальной. На самом деле реальные сообщения строятся из неравновероятных букв алфавита с наличием статистических связей между буквами. Поэтому энтропия реальных сообщений - H_р, оказывается много меньше оптимальных сообщений - H_о. Допустим, нужно передать сообщение, содержащее количество информации, равное I. Источнику, обладающему энтропией на букву, равной H_р, придется затратить некоторое число символов (сообщений) n_р, то есть I=n_pH_p . Если энтропия источника была бы Н₀, то пришлось бы затратить меньше символов на передачу этого же количества информации I= n₀H₀

.

Таким образом, часть символов n_р - n_о являются как бы лишними, избыточными. Таким образом, мера удлинения реальных сообщений по сравнению с оптимально закодированными и представляет собой избыточность D.

Но наличие избыточности нельзя рассматривать как признак несовершенства источника сообщений. Наличие избыточности способствует повышению помехоустойчивости сообщений. Высокая избыточность естественных языков обеспечивает надежное общение между людьми.

Математическая модель сообщения

Алфавит сообщения z={z₁,z₂,…,z_n)

Сигнальный алфавит x={x₁,x₂,…,x_m)

Пропускная способность каналов

Для организации эффективной передачи информации по каналу требуется решение следующих задач:

1. Определение максимально возможной скорости передачи данных по каналу;

2. Разработка кодов, позволяющих увеличить скорость передачи информации

3. Согласование канала с источником с целью передачи информации с минимальными потерями

Введение понятий энтропии, количества информации, скорости выдачи информации источником, избыточности позволяют характеризовать свойства информационных систем. Однако для сравнения информационных систем только такого описания недостаточно. Обычно нас интересует не только передача данного количества информации, но передача его в возможно более короткий срок; не только хранение определенного количества информации, но хранение с помощью минимальной по объему аппаратуры и т.п.

Важнейшей характеристикой канала является пропускная способность канала C, которая определяется как наибольшая возможная скорость передачи по данному каналу

C=v_xmax{I(Y,X } бит/сек ,

где v_x – предельная скорость передачи по каналу элементарных сигналов x₁, x₂,…, x_n.

Эту скорость можно выразить через среднюю продолжительность символов (импульсов) _ср передаваемого сигнала

v_x = 1/ _ср

Рассмотрим расчет пропускной способности для трех видов каналов:

1. дискретный канал без помех

2. дискретный канал с помехами

3. непрерывный канал с помехами