Інші типи псевдовипадкових послідовностей та їх порівняння
Сегментні ПВП. Сегментними називають ансамблі ПВП, які утворені із відрізків М-послідовностей великої довжини. Застосування таких ПВП було здійснено в роботі [5]. Тут М – послідовність довжини N=131071 символів розбивалась на сегменти довжиною N0=63 символи кожний. Було отримано L=2080 сегментів. Із них методом простого перебору були відібрані приблизно 1000 сегментів, нормовані бокові піки АКФ і ВКФ яких не перевищували 0,25. При великих значеннях N, L і N0 вибір сегментів методом простого перебору навіть при використанні комп’ютера є досить трудоємким, а в багатьох випадках безперспективним. Представляє інтерес визначити метод, який дозволяє найти аналітичні оцінки рівня максимальних бокових піків. Для знаходження такої оцінки можна використати циклічні властивості М-послідовності: сума по модулю 2 будь-якої М-послідовності S(k) з її зсувом S(k+j) також є М-послідовністю. Із цієї властивості видно, що і сума по модулю 2 двох сегментів є сегментом тієї ж М-послідовності, але з іншим зсувом. ВКФ сегментів sp(t) і sq(t) в дискретних точках τ=m τ0 має наступний вид:
(7.35)
Використовуючи сформульовану вище властивість сегментів М-послідовності, із (7.35) отримуємо:
(7.36)
-l-й
сегмент вихідної М-послідовності довжини
N0-m.
Таким чином, оцінка рівня максимальних бокових піків АКФ і ВКФ сегментів еквівалентна знаходженню значення максимального бокового піку серед всіх неперіодичних АКФ, які відповідають вихідній М-послідовності і всіх її циклічних зсувів. Позначимо через Rj(m) АКФ m-послідовноті S(k) довжиною N із зсувом j:
(7.37)
При зміні j від 0 до N-1 індекс l в (4.5) пробігає всі ті значення що і j, але в іншому порядку. Тому при такій зміні j сума в правій частині (7.37) дає значення всіх бокових піків неперіодичних АКФ сегментів довжини N-m. В свою чергу, зміна m від 0 до N-1 визначає всі сегменти із довжиною, яка змінюється від 1 до N. Ця властивість АКФ m-послідовностей і було використано для розрахунку максимуму суми:
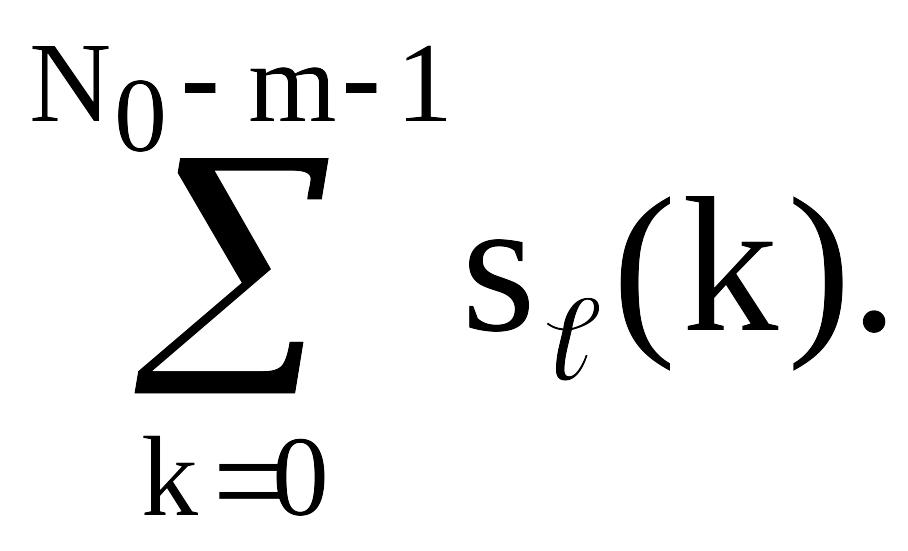(7.38)
Для N>15 великий об’єм розрахунків показав, що:
(7.39)
де а=1,26.
Таким чином, отримаємо верхню оцінку рівня максимальних бокових піків неперіодичних АКФ і ВКФ сегментів m-послідовностей:
(7.40)
Однак оцінка (7.40) при розрахунках практично не зустрічалась. Для більшості розглянутих М-послідовностей мала місце оцінка
(7.41)
Наведемо
приклади розрахунку АКФ і ВКФ двох
ансамблів послідовностей, які являються
сегментами М-послідовностей довжини
N=255 і N=511. Попередньо були визначені всі
значення сум
для
всіх можливих сегментів. В результаті
були уточнені коефіцієнти α. Виявилось,
що для вибраної m-послідовності
з N=255 коефіцієнт α=0,81, а для N=511 α=1,06.
Задавши значення Rpq(m)=0,4
N=255 для
α=0,81 і Rpq(m)=0,3
N=511
α=1,06, можна знайти довжини сегментів
N0,
які задовільняють цим значеннями і
кількість сегментів L. В результаті для
N=255 отримаємо N0=33;
L=12, для N=511- N0=80; L=9.
Ансамблі Камалетдинова відомі як інші бінарні ансамблі, що відрізняються від розглянутих лише структурою послідовностей, але не значеннями довжини L, об’єм К і максимуму кореляції ρmax. Тому особливий інтерес представляють ансамблі, які існують для довжин відмінних від довжин ансамблів Голда і Касамі.
В табл.7.3 приведено результати порівняння основних параметрів деяких ПВП: Голда, Касамі, Камалетдинова.
Таблиця 7.3.
Порівняння параметрів ПВП
Ансамбль |
Довжина |
Об’єм |
Квадрат максимуму кореляції ρmax |
Голд |
2n-1, n≠0 mod 4 7,31,63,127,511,1023 |
L+2=2n+1 |
|
Касамі |
2n-1, n-парне 15,63,255,1023 |
|
|
Камалетдинов 1 |
p(p-1), p- просте 42, 110, 342, 506, 930 |
|
|
Камалетдинов 2 |
p(p+1),p- просте 12,56,132, 380, 552, 992 |
|
|
,
.
.
.
.
.
.