6. Псевдовипадкові послідовності

Кореляційний аналіз та його застосування при дослідженні псевдовипадкових послідовностей полягає в кількісному вимірюванні ступеня подібності різних сигналів. Для цього використовуються кореляційні функції (КФ; англійський термін – correlation function, CF). Кореляційна функція детермінованого сигналу являє собою інтеграл від добутку двох копій сигналу, зсунутих одна відносно іншої на час τ [ 15]:

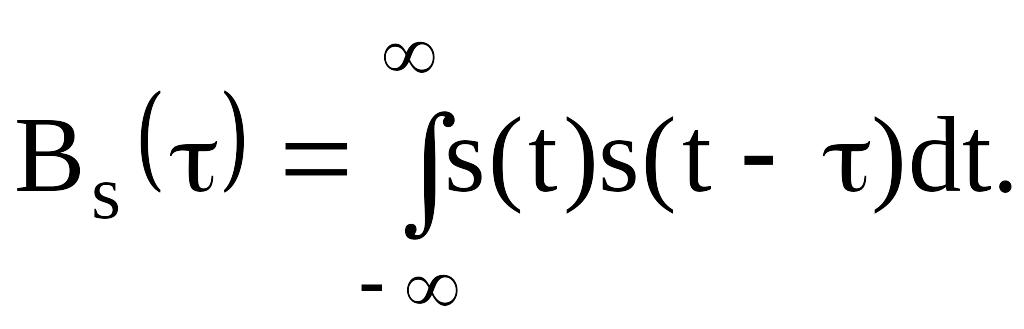(7.16)

Деякі властивості кореляційної функції приведені в табл. 7.2.

Якщо кореляційна функція вказує на ступінь подібності між зсунутими копіями одного і того ж сигналу, то вона являється автокореляційною функцією (АКФ), а випадку аналогічного порівняння двох різних сигналів – взаємною кореляційною функцією (ВКФ, cross-correlation function, CCF).

Однією з властивостей довільної двійкової періодичної послідовності, яка може бути використана в якості перевірки на випадковість (крім збалансованості та циклічності) являється кореляція. Якщо частина послідовності та її циклічно зсунута копія порівнюються поелементно, то бажано, щоб кількість співпадінь та неспівпадінь відрізнялись не більше ніж на одиницю:

|a-b| ≤1, ( 7.17)

де a,b – відповідно кількість співпадінь та неспівпадінь при зсуві копії відносно сигналу на час τ (значення τ не рівне періоду досліджуваної послідовності)

Таблиця 7.2.

Властивості кореляційної функції

№ п.п	Властивості	Формула
1	Значення КФ при τ = 0 дорівнює енергії сигналу
2	КФ є парною функцією свого аргументу τ
3	Значення КФ при τ = 0 є максимально можливим значенням
4	З ростом абсолютного значення τ КФ сигналу з кінцевою енергією загасає

Примітка:

1. Якщо сигнал s(t) не містить особливостей у вигляді дельта-функцій, його КФ являється неперервною функцією.

2. Якщо сигнал визначається у виді напруги, то розмірність його КФ становить В²с.

Для дискретної R_x(m) послідовності х(n), де n=0,1,…,N-1, періодична АКФ, яка дозволяє оцінити залежність між відліками х(n) в різні моменти часу, визначається за формулою:

_(7.18)

де

Функція R_x(m) являється парною, центрованою відносно значення R_x(0), яке, відповідно (7.18), дорівнює середній потужності з точністю до множника N:

_(7.19)

_{Для періодичного імпульсного сигналу, який представляє псевдовипадковий код, кожен з елементарних імпульсів такого сигналу називають кодовим символом (code symbol) або елементарним сигналом (ship). Нормована автокореляційна функція псевдовипадкового сигналу з одиничною тривалістю елементарного сигналу та періодом р елементарних сигналів може практично визначатись наступним чином:}

_{Rx( τ)=1/p*A ( 7.20)}

_{де А – різниця між кількістю відповідностей (співпадінь) та невідповідностей при порівнянні одного повного періоду послідовності з її модифікацією, отриманою шляхом циклічного зсуву на τ позицій}

_{Розглянемо приклад визначення періодичної АКФ наступної послідовності з метою перевірки її на випадковість}

1

1

1

0

0

1

0

_(7.21)

_{Нижче приведено залежність періодичної АКФ від зсуву між первинною послідовністю (3.21) та її копіями}

1	1	1	0	0	1	0
1	1	1	0	0	1	0
а	a	a	а	a	а	а

τ=0

S=7a (7.22)

1	1	1	0	0	1	0
0	1	1	1	0	0	1	0
b	a	a	b	a	b	b

τ=1

S =3a-4b=-1

1	1	1	0	0	1	0
1	0	1	1	1	0	0	1	0
a	b	a	b	b	b	a

τ=2

S=3a-4b=-1

Провівши аналогічні визначення для τ=3, 4, 5, 6, 7 отримаємо повні результати для даного прикладу, приведені в табл. 7.3

Таблиця 7.3

τ	0	1	2	3	4	5	6	7
S	7	-1	-1	-1	-1	-1	-1	7

З приведених результатів видно, що дана послідовність являється псевдовипадковою, тому що різниця кількості співпадінь та неспівпадінь (табл. 7.3) не перевищує одиницю при зсуві на час не рівний періоду досліджуваної послідовності.

В даному прикладі визначаласть періодична АКФ. При її визначенні ті значення зсунутої копії, які виходили за межі (4.7) первинної послідовності переносились (позначено стрілками) на початок зсунутої послідовності. Якщо ж таке перенесення не виконувати отримаємо аперіодичну АКФ. Нижче приведено визначення аперіодичної АКФ тієї ж послідовності (7.21 )

1	1	1	0	0	1	0
1	1	1	0	0	1	0
а	a	a	а	a	а	а

τ=0

S=7a

1	1	1	0	0	1	0
	1	1	1	0	0	1	0
	a	a	b	a	b	b

τ=1

S=3a-3b=0 (7.23)

1	1	1	0	0	1	0
		1	1	1	0	0	1	0
		a	b	b	b	a

τ=2

S=2a-3b=-1

Провівши аналогічні визначення для τ=3, 4, 5, 6 отримаємо повні результати для даного прикладу, приведені в табл. 7.4

Таблиця 7.4

τ	0	1	2	3	4	5	6
S	7	0	-1	0	-1	0	-1

Видно, що неперіодичній АКФ властивий коливальний характер зміни.

Більш зручно визначати кореляційні функції, зокрема АКФ, за допомогою формалізованих методів, наприклад, системи MATLAB. Але в системі MATLAB індекси можуть бути тільки додатні, тобто нижня границя в сумі (4.3) становить 1, тому автокореляційна функція розраховується за модифікованою формулою:

_(7.24)

де

Нижче приведено приклад визначення періодичної АКФ послідовності:

a=[1 1 1 -1 -1 1 -1 1 -1 1 1 1 -1 1 -1 1 -1 -1 -1 -1 …

1 -1 -1 1 -1 1 1 -1 -1] (7.25)

за допомогою наступного файлу системи MATLAB

% визначення періодичної АКФ

a=[1 1 1 1 1 -1 -1 -1 1 1 -1 1 1 1 -1 1 -1 1 -1 -1 -1 ...

-1 1 -1 -1 1 -1 1 1 -1 -1];a1=[ a a a]

b=[-1 -1 1 1 -1 1 -1 -1 1 -1 -1 -1 -1 1 -1 1 -1 1 1 1 -1 ...

1 1 -1 -1 -1 1 1 1 1 1 ] ;b1=[ b b b]; a2= fft( a1);

b2= fft( b1);c1=a2.*b2; c2=ifft(c1); s=1:93; plot(s,c2/93);grid on;

Аналогічно, за допомогою наступного файлу можна визначити значення аперіодичної АКФ для послідовності (7.25)

% визначення аперіодичної АКФ

x=[1 1 1 -1 -1 1 -1]

R=xcorr(x)./7

plot(R)

grid on

В результаті застосування даних файлів отримано (рис.7.17) нормовану періодичну та аперіодичну АКФ

Рис.7.17. Нормовані АКФ: (а) – періодична; (б) - аперіодична для псевдовипадкової послідовності при М=31

З приведеного графіка видно, що послідовність (7.25) являється псевдовипадковою, тому що значення періодичної АКФ задовільняють умові (4.2), тобто нормовані значення не перевищують величини 1/M= 1/31. Також

видно, що на відміну від періодичної АКФ для аперіодичної АКФ рівень бокових пелюстків носить коливальний характер.

Періодична та аперіодична ВКФ визначається аналогічно, як і АКФ, лише з тією різницею, що зсуву піддається не копія первинної послідовності, а інша послідовність з таким же періодом повторення:

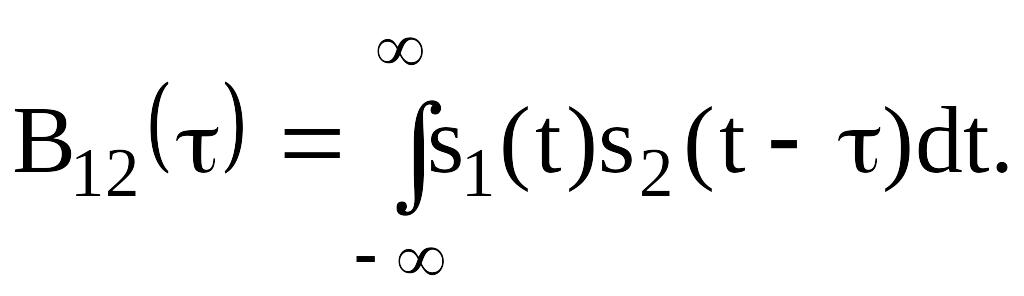(7.26)

Нижче при ведені деякі основні властивості ВКФ та їх відмінності від властивостей АКФ

1. , де Е₁, Е₂ – енергії сигналів s₁(t) i s₂ (t).

2. , тобто зміна знаку τ рівносильна взаємній перестановці сигналів.

3. Значення ВКФ при τ=0 нічим не виділяється; максимум може бути розміщений у будь – якому місці осі τ.

Для дискретної R_xу(m) послідовності х(n) і у(n), де n=0,1,…,N-1, періодична ВКФ, яка дозволяє оцінити залежність між відліками х(n) та у(n), в різні моменти часу, визначається за формулою:

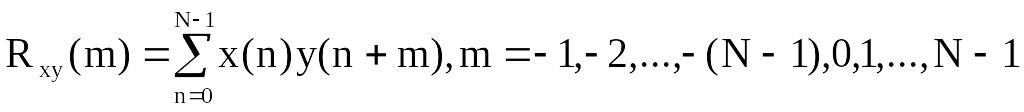_(7.27)

Нижче приведено приклад для визначення періодичної ВКФ послідовності

a=[1 1 1 1 1 -1 -1 -1 1 1 -1 1 1 1 -1 1 -1 1 -1 -1 -1 -1 1 -1 -1 1 -1 1 1 -1 -1]

почергово з кожною з двох псевдовипадкових послідовностей

b=[-1 -1 -1 1 1 1 1 -1 -1 1 -1 -1 1 1 -1 1 1 1 1 -1 ...

1 1 -1 -1 1 -1 -1 1 1 1 1] (7.28,а)

b=[-1 -1 -1 1 -1 -1 1 -1 1 -1 1 1 -1 -1 -1 -1 1 1 1 -1 ...

-1 1 1 -1 1 1 1 1 1 -1 1] (7.28,б)

на основі наступних файлів системи MATLAB

% визначення ВКФ двох послідовностей

a=[1 1 1 1 1 -1 -1 -1 1 1 -1 1 1 1 -1 1 -1 1 -1 -1 -1 ...

-1 1 -1 -1 1 -1 1 1 -1 -1];a1=[ a a ]

b=[-1 -1 -1 1 1 1 1 -1 -1 1 -1 -1 1 1 -1 1 1 1 1 -1 ...

1 1 -1 -1 1 -1 -1 1 1 1 1] ;b1=[ b b ]; a2= fft( a1);

b2= fft( b1);c1=a2.*b2; c2=ifft(c1); s=1:62; plot(s,c2/2);grid on;

% визначення ВКФ двох послідовностей

a=[1 1 1 1 1 -1 -1 -1 1 1 -1 1 1 1 -1 1 -1 1 -1 -1 -1 ...

-1 1 -1 -1 1 -1 1 1 -1 -1];a1=[ a a]

b=[-1 -1 -1 1 -1 -1 1 -1 1 -1 1 1 -1 -1 -1 -1 1 1 1 -1 ...

-1 1 1 -1 1 1 1 1 1 -1 1] ;b1=[ b b ]; a2= fft( a1);

b2= fft( b1);c1=a2.*b2; c2=ifft(c1); s=1:62; plot(s,c2/62);grid on;

В результаті застосування даних файлів отримано (рис.7.18) нормовані значення періодичної ВКФ приведених послідовностей

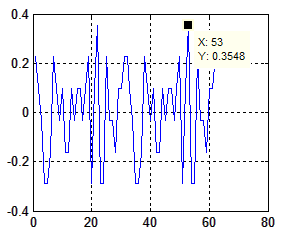
а) б)

Рис. 7.18. Приклад нормованої періодичної ВКФ послідовності (3.27) з послідовностями (3.28,а,б), відповідно

Порівнюючи дані, приведені на рис.7.18 бачимо, що для однієї і тієї ж послідовності періодичні ВКФ з різними псевдовипадковими послідовностями суттєво відрізняються. Якщо врахувати, що дані послідовності являються псевдовипадковими, то звідси видно, як багато залежить від правильного вибору псевдовипадкових послідовностей.

Показник розпізнавання вказує на вплив значень функції автокореляції та взаємної кореляції на функціонування системи зв'язку. Даний показник визначається як різниця значень основного піку періодичної АКФ та максимального бокового значення періодичної АКФ або ВКФ:

k_r = A_mo-A_mb або 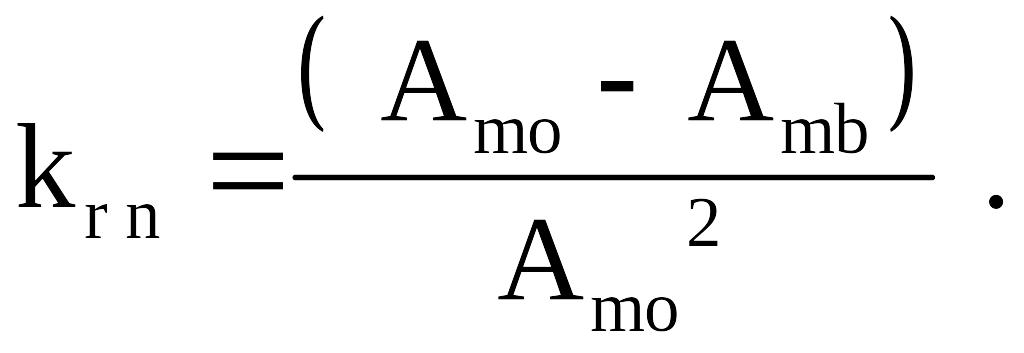( 7.29 )

де A_mo - значення основного піку періодичної АКФ; A_mb - значення максимального бокового значення періодичної АКФ або ВКФ; k_{r n} – нормоване значення показника розпізнавання.

Очевидно, чим більше значення показника розпізнавання, тим кращою являється кодова послідовність. Як показано на рис.7.17 максимальне нормоване значення, наприклад, для періодичної АКФ псевдовипадкової послідовності становить одиницю, а мінімальне - близьке до нуля, тобто показник розпізнавання незначно перевищує одиницю, що являється добрим показником. Навпаки, для отриманих значень ВКФ (рис.7.18) показник розпізнавання становить, орієнтовно, (1-0.35)=0.65 та (1-0.23)=0.77, що суттєво менше від його максимального можливого значення, яке близьке до одиниці.