Значення для формуючих поліномів

k=5	k=9	k=10
3;2 432; 321 431; 421	752; 742 76542; 75432 76543; 65432 764; 532 865; 431 854; 541 87653; 64321 87643; 65321 87543; 65421 872; 721 842; 751 87642; 75321 87542; 75421 87632; 76321 86532; 76431 851; 841 87651; 84321 86541; 85431 87631; 86321 86531; 86431 8765431; 8654321 87621; 87321	973; 731 843; 762 98643; 76421 98543; 76521 96543; 76541 9876543; 7654321 872; 832 952; 851 87652; 85432 942; 861 98642; 86421 97542; 86531 98732; 87321 98632; 87421 98432; 87621 9865432; 8765421 9765432; 8765431 961; 941 98651; 95421 98741; 96321 97641; 96431 9876541; 9654321 9876431; 9764321 98621; 98421
k=6
5; 1 532;431 541; 521
k=7
6; 1 4; 3 432; 543 631; 641 531; 642 521; 652 321;654 65321;65421 54321; 65432
k=8
654; 432 753; 531 653; 532 652; 632 76542; 64321 723; 651 761; 721 76521; 76321
	k=10
	7; 3 976; 431 985; 521 875; 532 854; 652 98754; 65321
k=9
5; 4 653; 643

Аналогічно, структури регістрів зсуву, які сформовані дзеркальними парами поліномів (рис.7.15,а,б), (рис.7.15,в,г), (рис.7.15,д,е), також являються дзеркальними. Як буде показано далі, також дзеркальними являються m-послідовності, отримані на основі дзеркальних регістрів зсуву.

а) б)

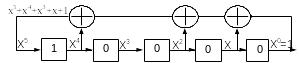
в) г)

д) е)

Рис. 7.15. Варіанти генераторів m-послідовностей, утворених на базі 5-ти бітового регістру зсуву

Найбільш складною проблемою являється генерація m-послідовностей. Отримати m-послідовність на виході регістру зсуву при заданому виді примітивного полінома та заданому початковому стані (значеннях символів 0 або 1 на виході кожного окремого регістра ) можна в принципі вручну. Але враховуючи великі масиви досліджуваних послідовностей доцільно застосовувати обчислювальну техніку. Наприклад, при використанні 5-ти бітового регістру зсуву отримаємо 31 варіант (далі вони будуть періодично повторюватись) початкових станів для кожного формуючого поліному, причому в даному випадку наявні 6 формуючих поліномів.

Спростити отримання m-послідовностей можна також за допомогою системи МATLAB. Наприклад, при використанні формуючого поліному х⁵+х³+1 його форму запису необхідно дещо змінити (в порядку збільшення степені х та з вказанням всіх кофіцієнтів), в результаті чого отримаємо формуючий поліном в наступному виді: 1*х⁰+0*х¹ +0*х²+1*х³+0*х⁴+1*х⁵. Тоді для одного з початкових станів (наприклад нульового стану) можна отримати один з варіантів m-послідовності за допомогою системи МATLAB наступним чином:

h = commsrc.pn('GenPoly', [1 0 0 1 0 1] , 'Shift', 0); set(h, 'NumBitsOut', 31)

m0=[generate(h)]'

В результаті при використанні генератора m-послідовностей, який містить k=5 регістрів зсуву, отримаємо псевдовипадкову послідовність довжиною М=31, що відповідає залежності (3.13)

m0=1 0 0 0 0 1 0 0 1 0 1 1 0 0 1 1 1 1 1 0 0 0 1 1 0 1 1 1 0 1 0

Псевдовипадковим послідовностям Голда властиві кращі кореляційні характеристики порівняно з m-послідовностями. Вони також формуються на основі пари m-послідовностей. Приклад формування послідовностей Голда на основі генераторів m-послідовностей (рис.7.15,а,г) приведено на рис. 7.16

Рис.7.16. Генератор кодів Голда на основі генераторів m-послідовностей

Генерація кодів полягає в наступному:

1. Необхідно вибрати пари m-послідовностей, необхідної довжини М, які властиво і формують ці послідовності

2. Шляхом додавання по модулю 2 двох m-послідовностей однакової довжини отримуємо перший код Голда тієї ж довжини

3. Наступні коди генеруються шляхом додавання по модулю 2 двох m-послідовностей одна з яких зсунута на один символ.

Між двома регістрами А і Б підтримуються однакові фазові співвідношення, а формуючі кодові послідовності мають таку ж довжину що і дві вихідні кодові послідовності, проте отримані послідовності Голда не являються максимальними. Код Голда може формуватись із будь-якого, відмінного від 0, стану регістрів, причому комбінація з всіх нулів являється недоцільною.