Технология транспорта нефти и газа

Лекция № 9 Гидравлический уклон.

Машиностроительный факультет гр.НР-31

К.т.н.Воробьёв В.В

Оглавление

1. Гидравлический уклон 2

2. Гидравлический уклон трубопровода с лупингом и вставкой 3

3. Всасывающий участок 5

4. Перевальная точка и расчетная длина трубопровода 6

5. Характеристика трубопровода 8

1. Гидравлический уклон

Отложим от начальной и конечной точек профиля трассы напоры (рис. 1):

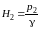и .

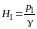Предполагается, что диаметр трубопровода – одинаковый по всей длине, местных сопротивлений нет, расход по длине не изменяется. Концы полученных отрезков H₁ и H₂ соединим прямой. Эта прямая называется линией падения напора или линией гидравлического уклона. Она показывает распределение напора по длине трубопровода. Тангенс угла наклона этой прямой называется гидравлическим уклоном i.

Р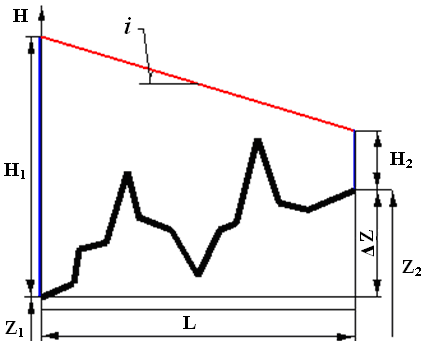 ис. 1. Определение гидравлического уклона

Из чертежа видно, что

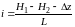. (3.33)

Но в соответствии с (3.14): H₁ – H₂ – Δz = h, следовательно, физический смысл гидравлического уклона – потеря напора на трение, приходящаяся на единицу длины трубопровода:

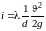; (3.34)

или по Лейбензону:

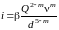. (3.35)

Удобно пользоваться следующей компактной формулой:

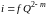. (3.36)

где 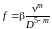– гидравлический уклон при Q = 1.

Прямая, соединяющая концы отрезков H₁ и H₂, называется линией гидравлического уклона. Она показывает распределение напоров (а, следовательно, и давлений) по длине трубопровода.

2. Гидравлический уклон трубопровода с лупингом и вставкой

Если на каком-либо участке трассы проложен параллельный трубопровод (лупинг) или трубопровод другого диаметра (вставка), гидравлический уклон на нем будет отличаться от гидравлического уклона магистрали.

Найдем соотношения между гидравлическими уклонами лупинга, вставки и магистрали. Будет считать, что режимы движения нефти в них одинаковы (рис. 2).

Р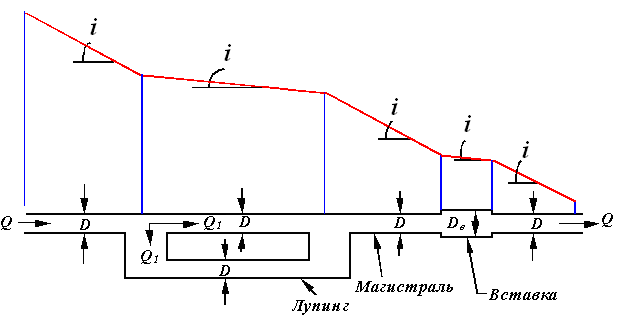 ис. 2. Гидравлический уклон на различных участках трубопровода

Пользуясь обозначениями, указанными на рис. 2, рассчитываем:

гидравлический уклон магистрали

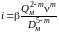; (3.37)

гидравлический уклон лупинга

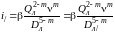; (3.38)

Учитывая, что Q₁ + Q₂ = Q, получим:

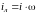, (3.39)

где ; ; .

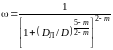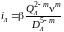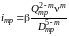Приведём более подробный вывод значения ω. Так как величина гидравлического уклона на основной трубе и на лупинге одинакова (параллельные трубопроводы), то i₁ = i_л. Запишем формулу Лейбензона для трубы и лупинга и выразим расходы в трубе и в лупинге:

, ,

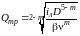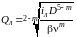или

, .

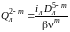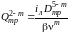Исходя из баланса расходов:

.

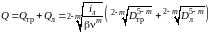Возведём Q в степень 2 – m:

,

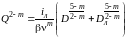и выразим отсюда i_л:

,

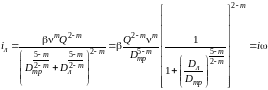где .

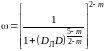Если , то .

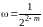В этом случае при ламинарном режиме 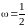, при турбулентном режиме в зоне Блазиуса ω = 0,297, для квадратичной области ω = 0,25.

Аналогично можно вывести для вставки

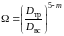; (3.40)

. (3.41)

Потеря напора на трение для трубопровода с лупингом будет складываться из потерь напора на участках одиночного и сдвоенного лупингов:

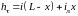, (3.42)

где x – длина лупинга.

Учитывая (8), можно также написать, что

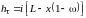. (3.43)

Полная потеря напора для трубопровода с лупингом

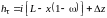. (3.44)

Для трубопровода со вставкой выражение для потери напора имеет аналогичный вид.

Далее для краткости будет писать

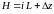, (3.45)

имея в виду, что при необходимости всегда L можно заменить на L – x(1 – ω) или на L – x(1 – Ω).

Если надо потерю напора выразить в зависимости от Q, то будем пользоваться формулой

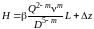(3.46)

или

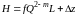. (3.47)