2.1. Розробка математичних моделей визначення місця розташування повітряних об'єктів

Однієї з основних задач РЛС є виявлення об'єкта в заданому просторі. Ця задача зводиться, по суті, до задачі виявлення відбитого від об'єкта радіолокаційного сигналу, спостережуваного на тлі шумів. Обробка сигналів у тієї або іншій формі містить у собі розв'язок задачі виявлення.

Радіолокаційне й радіонавігаційне спостереження завжди супроводжується цілим рядом випадкових перешкод. На корисні сигнали впливають шуми, які ухвалюються антеною з навколишнього простору, а також утворюються в приймачі. Крім того, самі прийняті радіолокаційні й радіонавігаційні сигнали, як правило, флуктуируют. Так, флуктуації відбитих сигналів обумовлені флуктуаціями мети. При відбитті радіохвиль від суши або від моря флуктуації прийнятих сигналів викликані зміною властивостей поверхні, що відбиває (наприклад, через хвилювання моря) і рухом випромінювача. Проходження радіохвиль через турбулентну атмосферу, коефіцієнти переломлення й поглинання якої неконтрольовано міняються, також приводить до флуктуацій сигналу. У силу цих причин при обробці радіолокаційної й радіонавігаційної інформації широко використовують методи теорії ймовірностей, теорії випадкових процесів і математичної статистики, а саме приймання сигналів, у тому числі і їх виявлення, розглядається як деяка статистична задача.

Проблема визначення місця розташування об'єкта або проблема містовизначення, зводиться до визначення (виміру) деяких геометричних величин, що однозначно характеризують місце об'єкта в просторі. До них ставляться, насамперед, довжина траєкторії поширення радіохвиль, або дальність, і напрямок на випромінювач радіохвиль. Визначення цих величин, називане радіодальнометрією і радіопеленгацією відповідно, здійснюється за допомогою радіопристроїв — радіодалекомірів і радіопеленгаторів. Кут між початковим напрямком і шуканим називається пеленгом. При пеленгації в горизонтальній площині в якості початкового ухвалюють північний напрямок географічного меридіана [5 - 8]. За позитивний напрямок відліку пеленга вибирають напрямок обертання годинної стрілки (рис. 2.1).

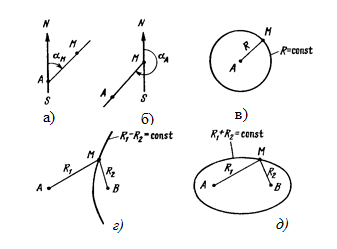
Рис. 2.1. Діаграми визначення геометричних величин і ліній положення

За допомогою радіопристроїв можна визначити наступні геометричні величини:

• пеленг х_м шуканої точки М з фіксованої точки А (рис. 2.1,а);

• пеленг фіксованої точки А із шуканої точки М (рис. 2.1,б);

• відстань R від шуканої точки М до фіксованої точки А (рис. 2.1, в);

• різниця відстаней від шуканої точки М до двох фіксованих точок А и В (рис. 2.1, г);

• суму відстаней від шуканої точки М до двох фіксованих точок А и В (рис. 2.1, д).

Кожному обмірюваному значенню якої-небудь із перерахованих величин відповідає лінія положення — геометричне місце точок, для яких геометрична величина, що визначає місце розташування об'єкта, постійна. При постійному пеленгу шуканої точки з фіксованої (рис. 2.1, а), як і при постійному пеленгу фіксованої точки із шуканої (рис. 2.1, б), лінії положення є прямими. При постійній відстані від шуканої точки до фіксованої лінія положення являє собою окружність із центром у точці А и минаючу через точку М. При постійній різниці відстаней від шуканої точки до двох фіксованих точок лінія положення є гіперболою, що проходить через точку М. Фіксовані точки А и Б — фокуси гіперболи. При постійній сумі відстаней від шуканої точки до двох фіксованих точок лінія положення є еліпсом, що проходять через точку М. Точки А и Б — фокуси еліпса.

При містовизначенні об'єкта в просторі постійному значенню кожної з перерахованих геометричних величин відповідає поверхня можливих місць розташування об'єкта, яка називається поверхнею положення. Постійному значенню відстані від фіксованої точки до шуканої відповідає поверхня положення у вигляді сфери. При постійнім значенні суми відстаней від шуканої точки до фіксованих точок поверхнею положення є еліпсоїд. При постійнім значенні пеленга в горизонтальній площині шуканої точки з фіксованої точки поверхнею положення буде вертикальна площина, що проходить через ці точки.

Перетинання двох поверхонь положення дає лінію положення в просторі. Точка перетинання лінії положення й третьої поверхні положення визначає місце розташування об'єкта в просторі. Якщо, наприклад, використовувати дальномерно-пеленгаційний метод, то місце розташування об'єкта дає точка перетинання прямій зі сферою. У цьому випадку для однозначного визначення напрямку на об'єкт необхідно здійснити пеленгацію у двох пересічних площинах, як правило — горизонтальної й вертикальної. Кут - між північним напрямком географічного меридіана й проекцією напрямку на об'єкт на горизонтальну площину називається азимутом. Кут - між напрямком на об'єкт і горизонтальною площиною називається кутом місця. Відстань R від радіолокатора до об'єкта називається похилою дальністю. Задача містовизначення об'єкта в просторі дальномерно-пеленгаційним методом зводиться до виміру трьох координат: похилої дальності, азимута й кута місця.

Чим більше зроблене отсчетов, тем менше дисперсія помилки, обумовленої дією шумів. Однак процес виміру вимагає часу, а за цей час може змінитися сама вимірювана величина. Останнє може привести до додаткової помилки, яку звичайно називають динамічною. Щоб зменшити цю помилку, при обробці відліків слід використовувати певні припущення про закон зміни в часі випадкової величини, що підлягає виміру, тобто ввести модель руху мети. Оптимізація обробки полягає в забезпеченні мінімуму середнього квадрата результуючої помилки стосовно до обраної моделі руху. Вибір моделі має велике значення при оптимізації обробки. Модель повинна хоча б грубо враховувати маневр мети й, не ускладнюючи розрахунків, приводити до практично реалізованих схемних розв'язків. Такій вимозі задовольняють моделі руху з випадковими незалежними приростами, на базі яких будується подальший аналіз. Уведемо поняття приростів вимірюваної величини за час між відліками [22 - 25]. Під відліком тут розуміється оцінка, обумовлена за час, протягом якого параметр ( можна вважати незмінним. При цьому вважаємо, що відліки проводяться не обов'язково по одному, але можуть проводитися по групі імпульсів.

Першим приростом вимірюваної величини за час між відліками будемо називати різниця її дійсних значень для m-го й (m-1)-го відліків (2.1):

(2.1)

другим приростом — відповідна зміна першого приросту

(2.2)

Модель слушна при досить різноманітних законах руху стрибкоподібного характеру. Прийняте, що дисперсія першого приросту у всіх точках Dw = 1. Початкова координата рівна ₀, початкова швидкість дорівнює нулю. Збільшення дисперсії Dw із часом характеризує нестаціонарність а_т - стационарни лише перші прирости _m.

Друга модель руху, на відміну від першої, дозволяє врахувати поступовий характер зміни координати, пов'язаний з більш плавною зміною перших приростів ₁ швидкості. Недоліком розглянутої моделі є те, що вона не враховує обмеження максимальної швидкості руху, характерного для реальних цілей.

Користуючись цими міркуваннями й уводячи результати відліків, можна послідовно визначати відповідні оптимальні оцінки й дисперсії. Кожна наступна оцінка складається із прогнозованої по попереднім відлікам оцінки _ін і сигналу помилки Dm, помноженого на ваговий множник (2.3)

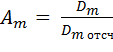. (2.3)

Оскільки відліки вводяться послідовно, до моменту одержання i-й оцінки немає необхідності зберігати в пам'яті обчислювального обладнання результати попередніх відліків, досить зберегти попередню оптимальну оцінку _m-1 і її дисперсію Dm-1.

Описана послідовна обробка не є єдино можливою. Зберігши в пам'яті обчислювального обладнання t відліків, можна, наприклад, одержати відразу t оцінок: а_1, а₂, ... ...,at, у тому числі оцінки параметрів від а₀ до а_x більш точні, чому отримані по меншій сукупності відліків. Однак оцінка а_т виявиться такий же, як і при послідовній обробці. Оскільки уточнення попередніх оцінок найчастіше не представляє самостійного інтересу, доцільно використовувати послідовну обробку.

Реальну атмосферу (тропосферу й іоносферу) не завжди можна ототожнювати з вільним простором, тому що ефекти поширення радіохвиль у ній можуть суттєво впливати на одержання радіолокаційної інформації. Крім того, у радіолокаційних станціях використовуються обладнання з розподіленими параметрами (фідери, лінії затримки й т.п.), у яких мають місце ефекти, аналогічні ефектам поширення хвиль в атмосфері.

Найпростішим з ефектів поширення радіохвиль є відмінність фазової швидкості в реальнім середовищі _ф від відповідної швидкості у вільному просторі. Нагадаємо, що фазова швидкість є швидкість переміщення геометричного місця точок з постійною фазою (хвильового фронту) при поширенні монохроматичної хвилі. Відмінність фазових швидкостей у реальнім середовищі й вільному просторі часто характеризують коефіцієнтом переломлення середовища (2.4)

. (2.4)

Якщо фазова швидкість залежить від частоти, то це вносить істотні додаткові ефекти при поширенні радіолокаційних сигналів.

Явище залежності фазової швидкості від частоти називається дисперсією хвиль. Середовища, у яких спостерігається дисперсія хвиль, називаються діспергірующіми. Вплив дисперсії хвиль проявляється при одночаснім поширенні декількох монохроматичних хвиль різних частот, що практично завжди має місце, тому що всякий радіосигнал може бути переданий тільки сукупністю (групою) монохроматичних хвиль.

У недіспергіруючей середовищу поширення сигналу не має ніяких особливостей у порівнянні з монохроматичною хвилею. Зокрема, швидкість поширення модуляції узкополосного сигналу, інакше групова швидкість _гр, дорівнює фазової швидкості кожної зі складових його монохроматичних хвиль.

У діспергіруючей середовищу монохроматичні хвилі групи поширюються з різними фазовими швидкостями. Це є причиною того, що фазові співвідношення між спектральними компонентами сигналу міняються. З'ясуємо, до чого приводить ця особливість поширення сигналу в диспергіруючей середовищу (рис. 2.2) [15, 17].

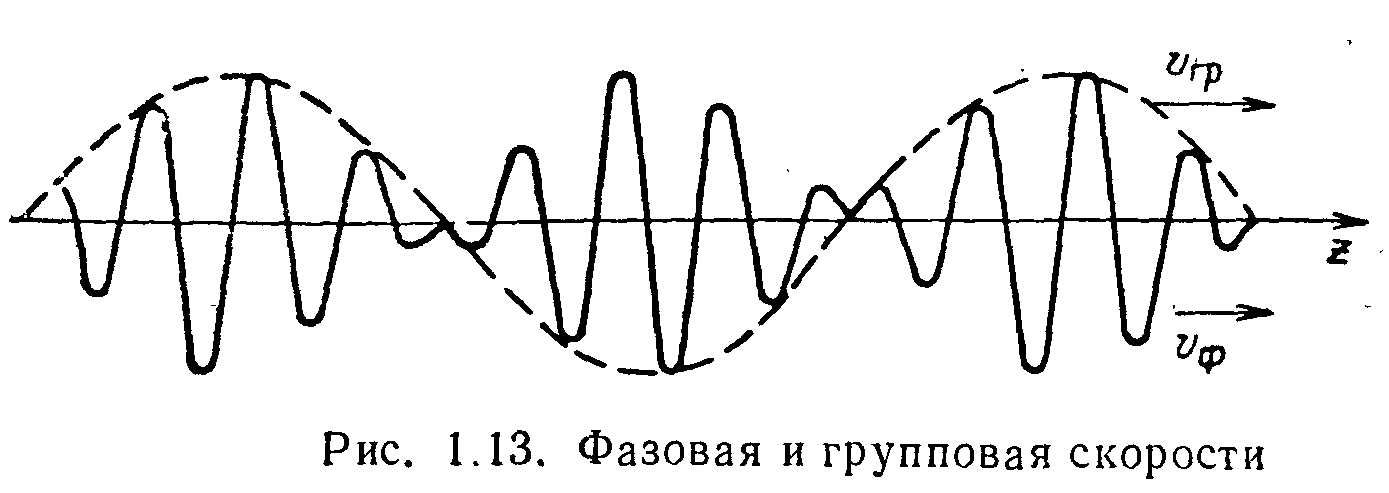
Рис. 2.2. Ілюстрація фазової й групової швидкості

Для простоти розглянемо випадок, коли група полягає всього із двох хвиль однакової амплітуди із близькими частотами коливань, що поширюються з фазовими швидкостями _ф1 і _ф2 у напрямку зростання координати. Сумарне коливання

(2.5)

де ; можна представити у вигляді (2.6)

(2.6)

З останнього зоотношения видне, що функція, що обгинає амплітуди

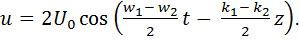(2.7)

переміщається уздовж осі Z зі швидкістю

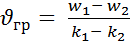(2.8)

А миттєві значення визначаються так

.

Фазова швидкість визначається співвідношенням 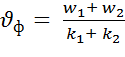(2.9)

(2.9)

Враховуючи близькість частот, одержимо

(2.10)

Таким чином, у діспергірующей середовищу фаза, що обгинає сигналу й, коливань поширюються з різною швидкістю. Відмінність швидкостей поширення фази, що обгинає й, коливань у діспергірующему середовищу було розглянуто щодо монохроматичної хвилі у два послідовні моменти часу [17, 22]. У просторі точок коливання складаються у фазі. У наступні моменти часу взаємне розташування хвиль зміниться. Через час ti максимуми обох хвиль зійдуться в точці А', вилученої від точки А на відстань λ₁ убік, протилежну напрямку руху хвиль. Розглянуті математичні моделі дозволяють надалі побудувати структурні, інформаційні й програмні моделі моніторингу радіолокаційної обстановки.