3.2. Розробка основних алгоритмів розрахунків просторових характеристик об'єктів у радіолокаційних комплексах

Алгоритми розрахунків просторових характеристик в області навігації й радіолокації ґрунтуються на визначенні геометричних характеристик фігур у гіперпросторі факторів [5, 13, 27]. До таких фігур ставляться куб, куля, піраміда й інші.

Побудова куба не викликає особливих утруднень, якщо є функція для побудови в просторі трикутника по трьом заданим точкам. Кожна квадратна грань куба може бути представлено у вигляді двох трикутників, що доповнюють. Таким чином, для побудови куба знадобиться відобразити в просторі 12 трикутників.

Побудова сфери й піраміди вимагає додаткових зусиль. Сферу будемо спрощено відображати у вигляді набору чотирикутників, кожний з яких будується так само, як і грані куба – із двох взаємодоповнюючих трикутників. Чотирикутники утворюються, якщо розбити поверхня сфери паралелями й меридіанами. Простір між паралелями назвемо шаром, а простір між меридіанами – часток (рис. 3.3).

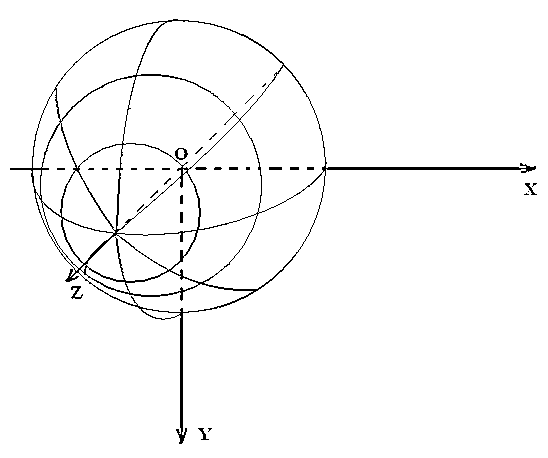
Рис. 3.3. Методи побудови сфери чотирикутниками

Кількість паралелей і меридіанів буде визначати якість відображення сферичної поверхні – чому їх більше, тем вище якість. Однак, при цьому потрібно більше часу на відображення сфери. Тому для цього класу можна передбачити можливість обчислювати координати вершин і нормалей заздалегідь, а потім багаторазово використовувати ці координати в процесі рис.вання. Нижче наведена блок-схема алгоритму обчислення координат вершин сфери (рис. 3.4). Для зберігання координат вершин використовується двовимірний масив Vert[i][j], а для зберігання нормалей – Norm[i][j].

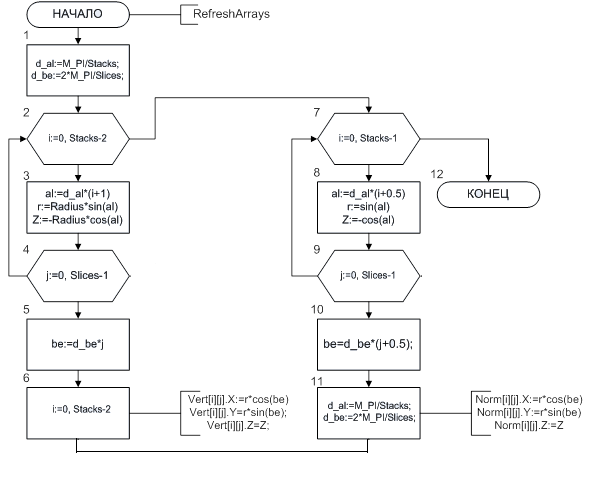
Рис. 3.4. Обчислення вершин і нормалей сфери

Піраміда будується аналогічно, але масиви Vert і Norm одномірні, тому що в правильній піраміді вісь обертання одна (рис. 3.5).

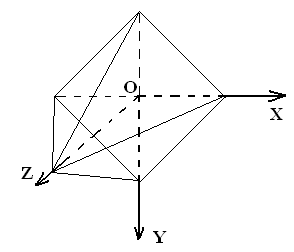
Рис. 3.5. Побудова радіолокаційної піраміди

На рис. 3.6. показана блок-схема алгоритму розрахунків координат вершин основи (Vert) і нормалей бічних поверхонь (Norm) піраміди.

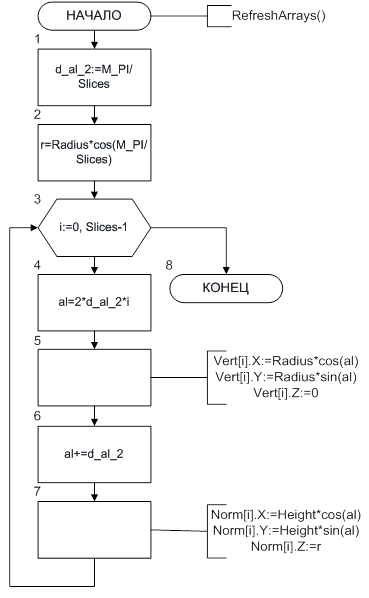
Рис. 3.6. Обчислення вершин і нормалей правильної піраміди

Тепер розглянемо аналітичні засоби обчислення й перетворення гіперфігур, що характеризують положення об'ємного об'єкта в просторі при його виявленні засобами радіолокації.

Н ехай – матриця виду до перетворення, а – матриця виду після переміщення. Тоді для перетворення системи координат необхідно зробити добуток матриці переміщення на матрицю :

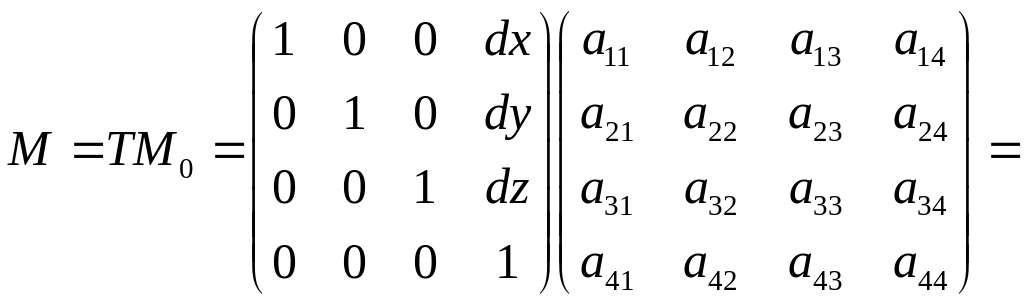_(3.4)

Н ехай – матриця виду до масштабування, а – матриця виду після масштабування. Тоді для масштабування системи координат необхідно зробити добуток матриці масштабування на матрицю :

_(3.5)

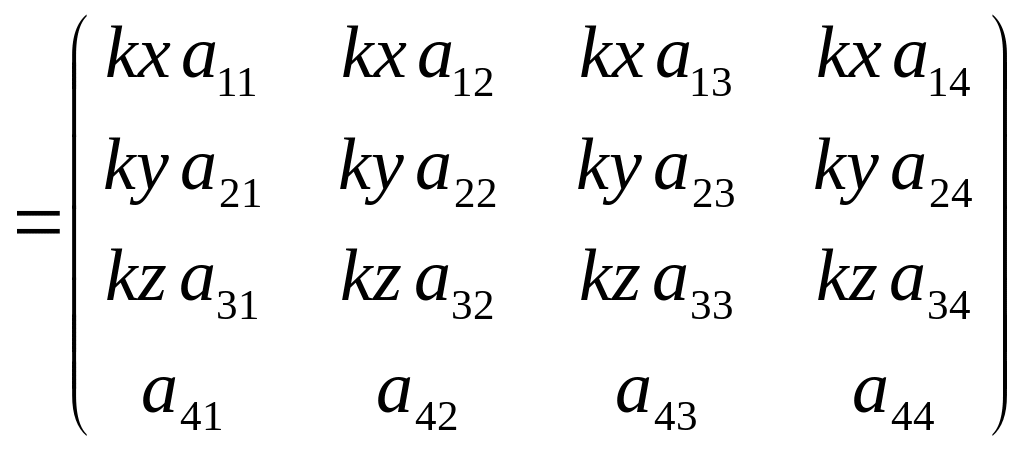
Р озглянемо поворот навколо довільної осі. Нехай вектор  це вектор, що задає вісь, навколо якої потрібно зробити поворот. Нехай – проекція вектора на площину yoz (рис. 3.7).

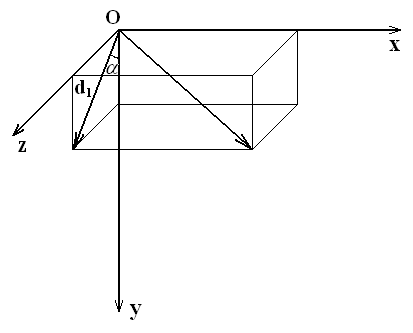
Рис. 3.7. Перший етап повороту навколо довільної осі

Якщо , то вектор практично належить осі Ox і поворот щодо вектора збігається з поворотом щодо осі Ox. А якщо ні, то виконується така послідовність дій:

• поворот навколо осі Ox на деякий кут 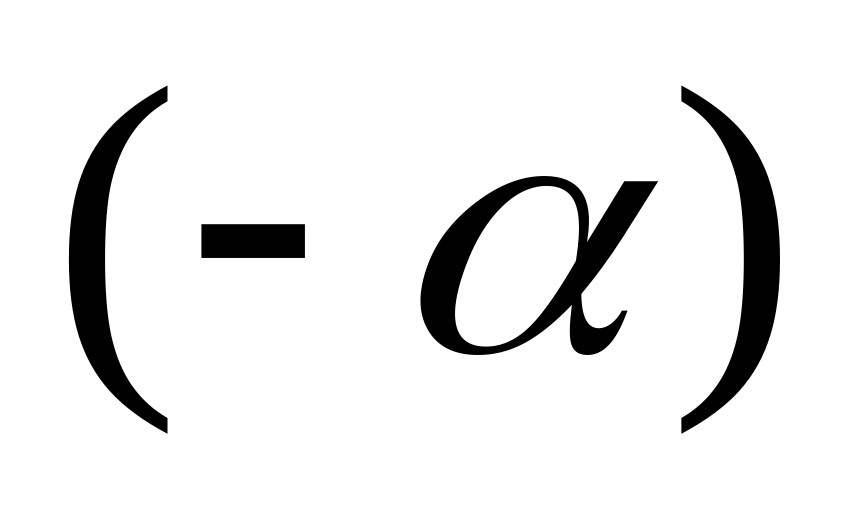- матриця повороту 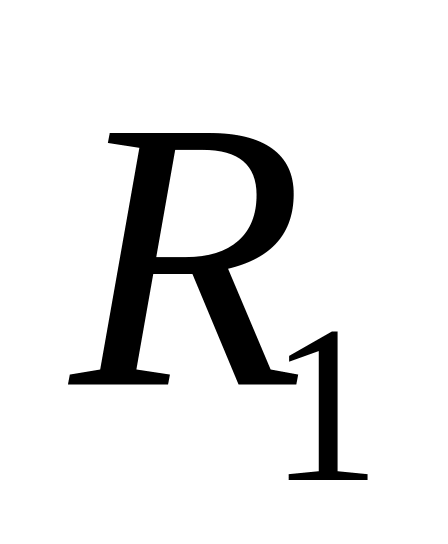_,- після якого вектор буде належати площині xoy;

• поворот навколо осі Oz на деякий кут , після чого вектор буде належати осі Ox (матриця повороту );

• поворот навколо осі Ox на заданий кут 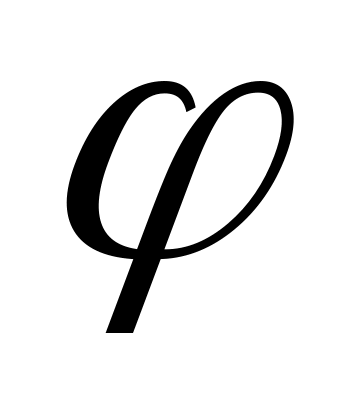(матриця повороту );

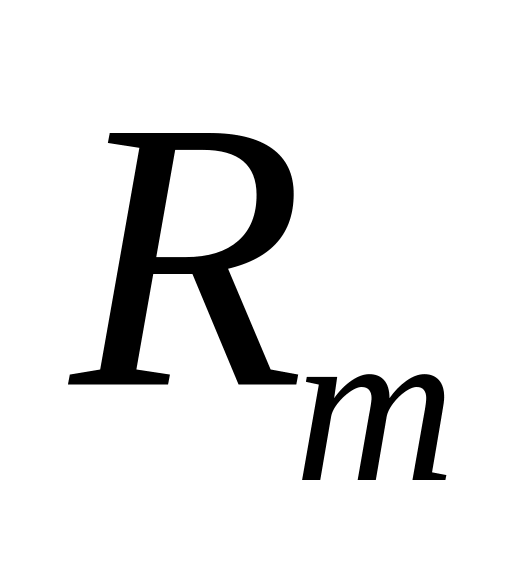• поворот навколо осі Oz на кут (матриця повороту );

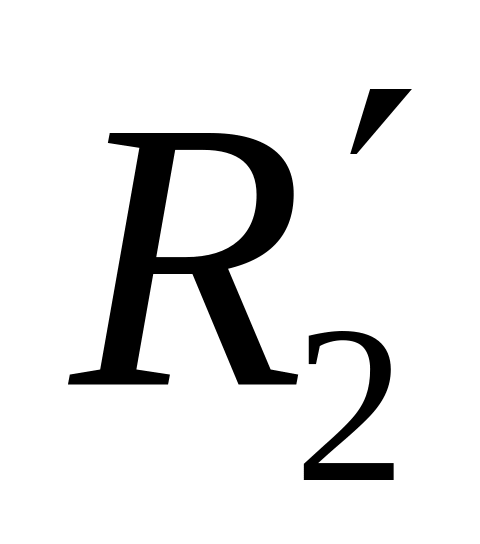• поворот навколо осі Ox на кут , після чого вектор ухвалює колишнє положення (матриця повороту ).

Після зазначених дій виконується другий етап повороту, як показано на рис. 3.8.

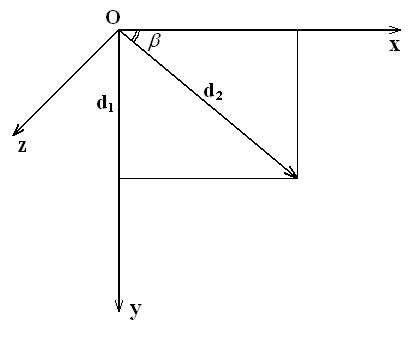
Рис. 3.8. Другий етап повороту

У матричному виді другий етап повороту буде мати вигляд 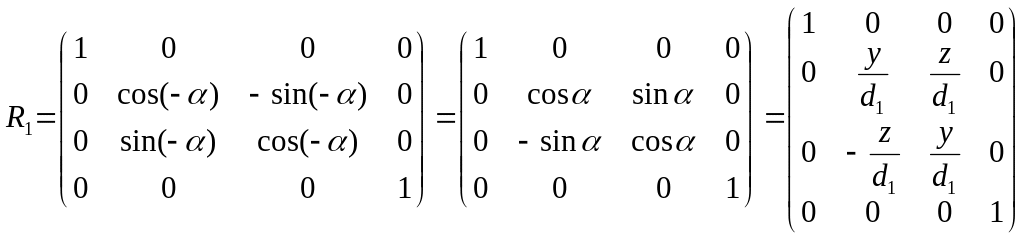(3.6)

_(3.6)

Нехай – довжина вектора ( ), тоді

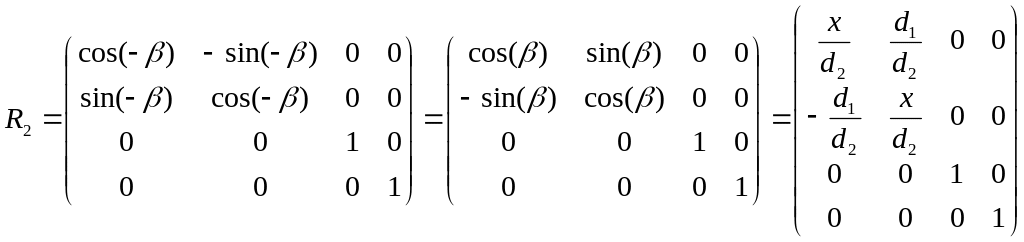
Щоб поворот здійснювався за правилом буравчика ( за годинниковою стрілкою, якщо дивитися уздовж осі Ox), необхідно виконувати його паралельно в площині yoz не на кут , а на кут (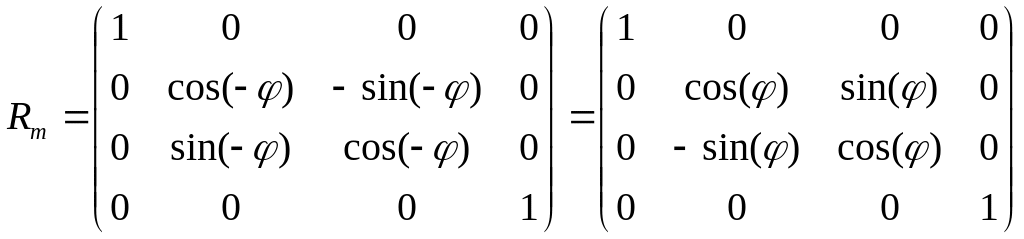3.7)

_(3.7)

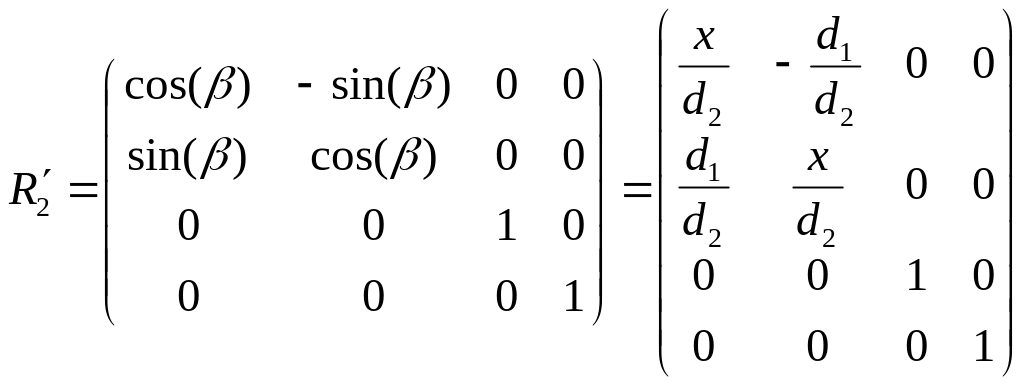
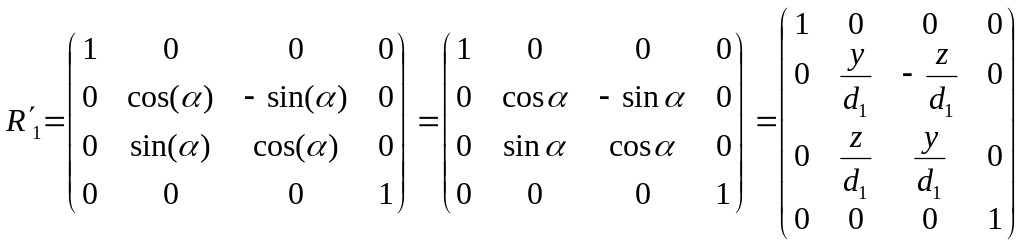
Наведені аналітичні вираження добре алгоритмизируются, що дозволяє розробляти на їхній основі програмні модулі розрахунків характеристик як точкових, так і об'ємних об'єктів, що рухаються. У дипломній роботі ( як приклад) використаний найпростіший випадок перетворення положення об'єкта в прямокутних координатах і горизонтальна проекція об'єкта на площину XOY.