Алгоритм вычесления нечёткого критического пути - Федорова И.В

АЛГОРИТМ ВЫЧИСЛЕНИЯ НЕЧЁТКОГО КРИТИЧЕСКОГО ПУТИ

Фёдорова И. В.1

(Воронежский государственный архитектурно – строи- тельный университет, Воронеж)

FEDOROVA_I@list.ru

Рассмотрим проект, состоящий из набора операций (работ), представленный в виде сети (U, D), |U| = n без контуров с правиль- ной нумерацией вершин. Среди множества вершин выделены

входы сети U0 и выходы сети Un . При этом дуги сети соответст-

вуют операциям, а вершины - событиям (моментам окончания одной или нескольких операций). В четком случае для каждой

операции (i; j) задана её продолжительность tij . Методы описания

и исследования сетевых графиков изучаются в теории календарно- сетевого планирования и управления [2,3,4].

Предположим, что выполнение комплекса операций (проекта) начинается в нулевой момент времени. Обозначим Ui− - множест-

во событий (вершин) j сети, для которых существует дуга ( j, i); Ui+

- множество событий (вершин) j сети, для которых существует дуга

( i, j).

В [1] рассмотрен нечёткий случай, при котором относительно продолжительностей операций имеется нечёткая информация,

заданная функциями принадлежности μij (·) : Â+ ® [0;1] нечёт-

кой продолжительности операции ( i, j), i, j U , которая может быть получена от экспертов в ситуации, когда проект и каждая операция являются уникальными.

В [1] для функций принадлежности нечёткого раннего времени свершения события i U - μi− (t) , нечёткой длины критического пути μT (T ) ,нечёткого позднего времени свершения события i U - μi+ (t) , нечёткой длины максимального пути из вершины i -

1 Научный руководитель д.т.н., профессор Баркалов С. А.

Таким образом формула (1) может быть записана в следующем виде:

(13) μi+ (t) = max min[μT (T ); μimax (T - t)],

T

где после преобразований аналогичных преобразованиям для формулы (1),

4

каждого допустимого j при фиксированном t происходит оптими- зация по одной переменной при нахождении Bj (t) и оптимизация

по двум переменным при нахождении Aj (t) , что позволяет реали-

зовать более простые и эффективные алгоритмы нахождения

μi− (t) и μimax (t) .

Величину μi t (0) Î[0;1] можно интерпретировать как степень

принадлежности i-го события критическому пути, i U. Тогда при

выполнении проекта первоочередное внимание должно уделяться событиям, у которых степени принадлежности критическому пути равны единице или близки к ней.

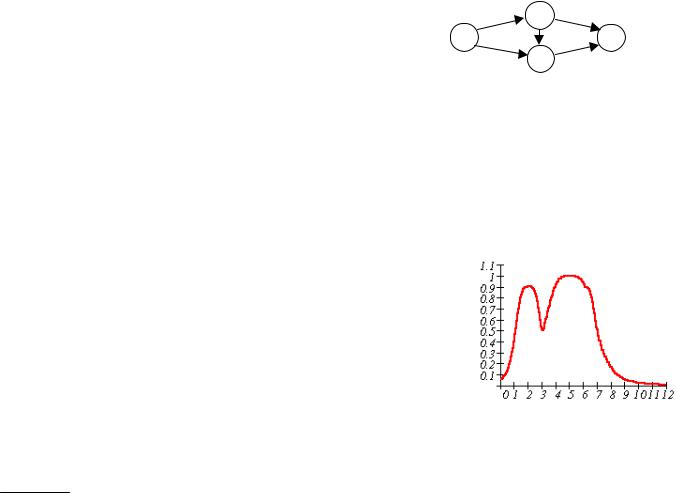
Рассмотрим иллюстративный пример нахождения функции принадлежности нечёткого критического пути для сети, представ- ленной на рис. 1.

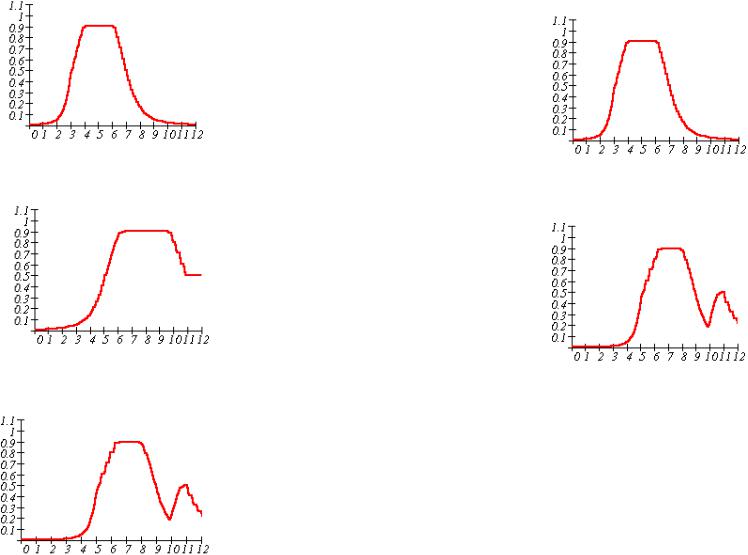
На рис. 2 - 3 изображены графики функций

μmax (t) = max max[min(μ (t ); μ− (t ))];

j Ui− t j +t ji =t ji ji j j

μmin (t) = min max[min(μ (t );μ − (t ))] для вершины i=2, а на

j Ui− t j +t ji ≤t ji ji j j

рис. 4 - 5 для вершины i=3. На рис. 6 - 7 приведены графики μ2− (t)

иμ3− (t) соответственно. В данном случае μT (t) = μ3− (t) .

μmax (t)

t

Рис. 2