1.3. Универсальное уравнение состояния идеального газа

Подставляя (1.2) и (1.3) в (1.1), получим 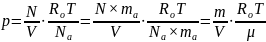, где m – масса газа, кг.

Отсюда получаем уравнение состояния идеального газа Клапейрона – Менделеева:

p·V = R₀T (1.4),

Используя величину «удельный объем»– отношение объема вещества к его массе. . (1.5)

получим это уравнение в виде p·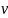 = T (1.6)

Удельный объём является величиной, обратной плотности , :

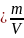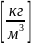v (1.7)

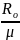Подставив R_μ = ,где R_μ 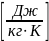- газовая постоянная данного газа, в (1.4), получим

(1.8)

В уравнениях (1.4), (1.6) и (1.8) p – давление[Па], V – объём[м³], – удельный объём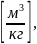 m–масса газа [кг], μ - молярная масса газа , Т – температура [К]

Например, для кислорода = = .

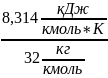Уравнение состояния описываются тремя параметрами: давлением, удельным объёмом и температурой. Два из них независимы, а третий определяется в зависимости от первых двух по уравнению (1.8).

Уравнение (1.8) носит обобщенный характер. Из него как частные случаи вытекают ранее полученные экспериментальными методами законы идеальных газов.

Изотермический процесс. Закон Бойля – Мариотта. T = const. pv = const (1.9)

Изобарический процесс. Закон Гей-Люссака. Р = const. 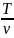= const (1.10)

Изохорический процесс. Закон Шарля. V = const. 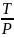= const (1.11)

1.4. Смесь идеальных газов

П од газовой смесью понимается смесь отдельных газов, не вступающих между собой ни в какие химические реакции. Каждый газ (компонент) в смеси независимо от других газов полностью сохраняет все свои свойства и ведет себя так, как если бы он один занимал весь объем смеси.

1.Сосуд наполнен двумя различными газами, разделёнными нематериальной перегородкой. Под действием давления справа и слева перегородка установится в положении, при котором р₁ = р₂ = р₀.

2.Пусть Т₁ = Т₂ = Т₀. Удалим перегородку. V_см = V₁ + V₂.

3.Поочерёдно откачаем один из газов, установятся парциальные давления р₁ и р₂.

Парциальное давление – это давление, которое имел бы каждый газ, входящий в состав смеси, если бы этот газ находился один в том же количестве, в том же объеме и при той же температуре, что и в смеси.

4.Сожмём газы до прежних объёмов. Парциальный объём (V₁ и V₂) – тот, который газ занимал бы при р = р_см и Т = Т_см.

Количество и температура первого газа в стадиях и 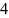одинаково. Из уравнения состояния для этих стадий p₁·V_см = p_см·V₁, отсюда p₁ = r₁ p_см.

Газовая смесь подчиняется закону Дальтона:

Общее давление смеси газов равно сумме парциальных давлений отдельных газов, составляющих смесь.

р_см = р₁ + р₂ + р₃ + . . .р_n = ∑ р_i , (1.12)

где р₁ , р₂ , р₃ . . .р_n – парциальные давления.

Состав смеси задается долями объемными r, r₁ = 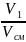; r₂ = ; (1.13)

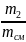массовыми g g₁ = ; g₂ = ; (1.14)

и мольными r₁^′: r₁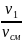^′ = ; r₂^′ = ; (1.15)

где V₁; V₂; V_см – объемы компонентов и смеси; m₁; m₂; m_см – массы компонентов и смеси; ν₁; ν₂; ν_см – количество вещества (киломолей) компонентов и смеси.

Для идеального газа по закону Дальтона объёмные доли равны мольным:

r₁ = r₁^′ ; r₂ = r₂^′ ; (1.16)

Так как V₁ +V₂ = V_см и m₁ + m₂ = m_см , то r₁ + r₂ = 1 , (1.17)

g₁ + g₂ = 1. (1.18)

Парциальное давление: p₁ = r₁ p_см.

Молярная масса смеси: μ_см = μ₁ r₁ + μ₂ r₂. μ_см = (1.19)

где: μ₁ , μ₂, μ_см – молярные массы компонентов и смеси.

Связь между объемными и массовыми долями следующее:

g₁ = r₁∙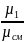 ; g₂ = r₂∙

Газовая постоянная смеси: R_см = g₁ R₁ + g₂ R₂ = R₀

R_см = 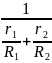. (1.21)

Удельные массовые теплоемкости смеси: с_{р см.} = g₁ с_р1 + g₂ с_р2. (1.22)

с_{v см.} = g₁ с_v1 + g₂ с_v2 (1.23)

Удельные молярные теплоемкости смеси: μс_{р см.} = r₁ μс_р1 + r₂ μс_р2. (1.24)

μс_{v см.} = r₁ μс_v1 + r₂ μс_v2 (1.25)