ПОверхностные явления и адсорбция

Коллоиды - высокодисперсные системы, наиболее существенные свойства которых определяются особенным состоянием вещества на границе раздела фаз. В процессе диспергирования в поверхностном слое увеличивается доля молекул, которые энергетически отличаются от частиц системы.

Обратимая изотермическая работа W образования единицы новой поверхности называется свободной энергией

W= - ΔA=σ·s,

где σ для границы раздела раствор-собственный пар (воздух) равна поверхностному натяжению - силе, которая действует на единицу длины контура, ограничивающего межфазную поверхность, Н/м, Дж/м²;

s - поверхность раздела фаз, м².

При переходе от индивидуальных растворов к растворам, поверхностноенатяжение, как правило изменяется.

Вещества, способные концентрироваться на границе раздела фаз, уменьшая σ, называются поверхностно-активными (ПАВ). Мерой излишнего содержания компонента раствора в поверхностном слое в сравнении с объемом является адсорбция Г.

Лабораторная работа №1 Исследование адсорбции пав на границе раствор-воздух

Цель работы: рассчитать значение предельной адсорбции Г_∞, поверхность, занимаемую молекулой адсорбата в поверхностном слое S₀, толщину адсорбционного слоя δ по экспериментальным данным.

Для измерения поверхностного натяжения можно воспользоваться методом максимального давления пузырька.

В этом случае σ определяется по давлению, при котором происходит отрыв пузырьков воздуха, выдуваемых в исследуемый раствор через капилляр.

Даление Р в момент отрыва пузырька максимальный и связан с поверхностным натяжением соотношением

σ = К·Р (1.1)

где К определяют путем измерения величины Р для жидкости с известным значением σ, например, воды, для которой мН/м при Т=298 К. Зная и , из уравнения (1.1) получим К.

Постоянная К зависит от формы капилляра, его среза и глубины погружения в раствор.

(1.2)

Оборудование и реактивы.

Прибор Ребиндера для определения поверхностного натяжения.

Растворы ПАВ 4-7 концентраций.

Дистиллированная вода.

Ход работы

Поверхностное натяжение определяют при помощи установки, предложенной Ребиндером (рис.1).

В сосуд 1 заливают воду или раствор так, чтобы край капилляра касался поверхности жидкости.

Краном эжектора 2 устанавливают постоянную скорость вытекания жидкости для обеспечения равномерного проскока пузырьков (1 проскок за 20 с). При этом фиксируют максимальный (h₁) и минимальный (h₂) уровни манометра. Измерения повторяют несколько раз до получения постоянных результатов.

Максимальное давление пузырьков определяют по разности уровней манометра Δh = h₂ - h₁ и рассчитывают величину σ, Н/м:

(1.3)

Сначала устанавливают Δh для дистиллированной воды, а затем для исследуемых растворов ПАВ (по указанию преподавателя), начиная с наименьшей концентрации.

При температуре, отличной от стандартной (298 К), σ определяют из соотношения , где - постоянная, равная температурному коэффициенту с обратным знаком.

Обработка экспериментальных данных

Рассчитанные по уравнению (4) значения σ используют для построения графика в координатах (рис.2).

Адсорбцию рассчитывают по уравнению Гиббса

(1.4)

П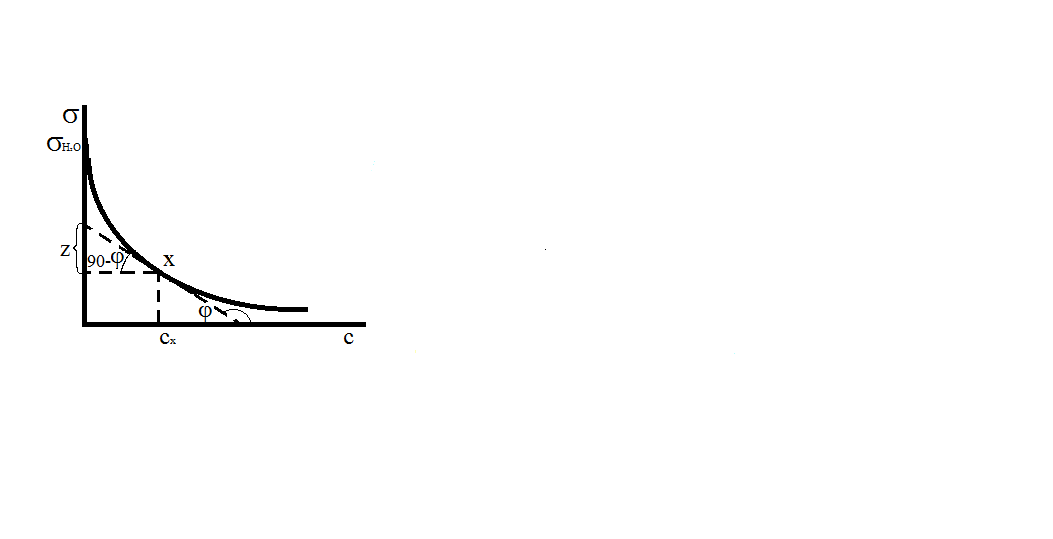 утем графического дифференцирования σ,с-зависимости определяют значение z. Если провести касательную к кривой в точке х, то тангенс ее угла наклонак оси абсцисс (угол ) будет равен .

Из графика видно, что

(1.5)

Рис.2 где z - отрезок, отсекаемый на оси ординат горизонтальной прямой, проведенной через точку х, и касательной к кривой в этой точке.

Подставляя значения z из (6) в уравнение (5) получаем Г, моль/м²:

(1.6)

О бработав указанным методом кривую в 8-10 точках, строят изотерму адсорбции (рис.2), по которой ориентировочно определяют предельную (максимальную) адсорбцию Г_∞, соответствующую образованию мономолекулярного слоя.

Рис.3. Изотерма адсорбции Ленгмюра, которой отвечают полученные данные, имеет вид

(1.7)

Уравнение Ленгмюра можно преобразовать в уравнение прямой (рис.4):

(1.8)

Рис.4 Отрезок, отсекаемый прямой на оси ординат, равен , где b - константа адсорбционного равновесия.

(1.9)

По рассчитанным значениям предельной адсорбции Г_∞ определяют площадь молекулы S₀ и толщину адсорбционного слоя δ, которая соответствует длине адсорбированной молекулы:

; (1.10)

где N_A - постоянная Авагадро;

M - относительная молекулярная масса;

ρ - плотность ПАВ.