1.4.1. Модули расчета параметров

Расчет параметров сетевого графа характеризуется своей спецификой и требует соблюдения определенных правил.

Рассмотрим далее в модульном варианте в формализованном представлении расчет каждого из параметров графа.

Модуль 1. Расчет ранних параметров

Ранние параметры отражают сроки начала и окончания работ при предельно ранних возможностях их выполнения с учётом заданной последовательности работ.

Для каждой работы, принадлежащей сетевому графу, сначала рассчитывается ее раннее начало, а затем - раннее окончание:

При расчете раннего начала определяющее значение имеет положение рассматриваемой работы (i, j) в сетевом графе: данная работа может иметь непосредственно предшествующие работы или не иметь их (выходить из исходного события - i =1).

Тогда работа, выходящая из исходного события, может начинаться с нулевого (0) момента времени ( =0, если i =1).

Та же работа, которая имеет одну или несколько непосредственно предшествующих работ, может начинаться только после наступления события, из которого эта работа выходит, то есть после наибольшего по продолжительности раннего окончания ( ) всех непосредственно предшествующих ей работ (max [ ], если i >1).

Примечание: если данной (i, j) – й работе непосредственно предшествует только одна, то раннее начало данной работы будет равно раннему окончанию непосредственно предшествующей, поскольку событие, в которое входят все непосредственно предшествующие работы, наступает мгновенно после выполнения всех этих работ ( = ).

В процессе расчета последовательно перебираются все без исключения работы, в том числе фиктивные. Расчет параметров ведется на графе - слева направо, а при работе с таблицей - сверху вниз.

Модуль 2. Определение продолжительности критического пути

Время критического пути определяется как минимально возможное время, в продолжение которого завершится весь состав работ сетевого графа в соответствии с его геометрией. Это время равно наибольшему времени ранних окончаний работ, входящих в завершающее событие сетевого графа:

= max [ ], j = m (завершающее событие); в то же время оно является наименьшим по величине, в течение которого будет выполнен весь комплекс работ сетевого графа.

От исходного до завершающего события имеется несколько путей, однако все они без исключения будут меньше критического пути или равны ему. Продолжительность критического пути будет равна суммарному времени работ, принадлежащих ему:

Модуль 3. Расчет поздних параметров

Поздние параметры отражают сроки начала и окончания каждой из работ сетевого графа при предельно поздних возможностях их выполнения с учетом предшествования и следования этих работ в сетевом графе.

Поздние сроки начала и окончания работ определяются из возможностей предельного сдвига вправо по временной оси сроков выполнения работ в такой степени, чтобы не изменилась величина критического пути. Этим требованием обусловливается логика расчетов поздних параметров: от завершающего к исходному событию сетевого графа, а также предшествование расчета времени позднего окончания (i, j) – й работы ее позднему началу, то есть для каждой работы, принадлежащей сетевому графу → .

В процессе расчета последовательно перебираются справа налево на сетевом графе или снизу вверх при работе с таблицей все без исключения работы, в том числе фиктивные.

При расчете позднего окончания определяющее значение имеет то, какое положение рассматриваемая работа (i, j) занимает в сетевом графе: входит ли она в завершающее или в промежуточное событие.

Если данная работа входит в завершающее событие, тогда ее позднее окончание не может выйти за пределы критического пути ( ). В противном случае, при условии, что за этой работой непосредственно следует несколько работ, которые могут начинаться (их позднее начало) в разное время, тогда, чтобы не изменился критический путь по величине, необходимо данную работу предельно поздно завершить так, чтобы ни одна из непосредственно следующих работ не сдвинулась по позднему началу, то есть позднее окончание данной работы должно быть равно наименьшему значению поздних начал работ, непосредственно следующих за данной ( =min [ ], если j < m).

Примечание: Если за данной (i, j) – й работой непосредственно следует только одна, то позднее окончание данной работы должно быть строго равно позднему началу непосредственно следующей работы ( ).

Все рассчитанные ранние и поздние параметры сетевого графа в графической интерпретации представлены на рис. 7.

Рис.7. Отображение ранних и поздних параметров на (i ,j) – й работе сетевого графа

Модуль 4. Расчет резервов сетевого графа

Резервы времени работ сетевого графа определяют возможные сдвиги соответственно начал и окончаний работ сетевого графа в пределах ранних и поздних параметров, характеризующих конкретную работу.

Полный резерв времени ( ) характеризуется возможным предельным сдвигом вправо по временной шкале сроков выполнения работ сетевого графа. Его величина определяется разностью либо между поздним и ранним началами данной работы, либо между поздним и ранним ее окончаниями. Эти разности должны быть строго равны:

= - = - .

Принцип расчета полного резерва времени по работе (i, j) в графической интерпретации представлен рис. 8.

Рис. 8. Графическая интерпретация расчета полного резерва времени работы (i, j)

Поскольку у работ, лежащих на критическом пути, = и = , следовательно, полные резервы времени всех работ, принадлежащих критическому пути, равны нулю:

.

Руководствуясь этим правилом, можно выделить работы критического пути. В некоторых сетевых графах может быть не один, а несколько критических путей.

Примечание: в сетевом графе могут быть работы, полные резервы времени которых равны нулю. Однако они не принадлежат критическому пути, а характеризуют только отсутствие резерва у конкретно взятой работы.

Частный резерв времени первого вида определяется возможностью изменения позднего начала работы (i, j) на более ранний срок без изменения поздних сроков окончания непосредственно предшествующих работ (рис. 9):

Рис. 9. Графическая интерпретация расчета частного

резерва времени первого вида работы (i, j)

Ч астный резерв времени второго вида определяется возможностью изменения раннего окончания работы (i, j) на более поздний срок без изменения ранних сроков начала непосредственно следующих работ (рис. 10):

- , если j = m,

=

- , если j < m

Рис. 10. Графическая интерпретация расчета частного

резерва времени второго вида работы (i, j)

Свободный резерв времени работы определяется дополнительным временем (сверх продолжительности выполнения данной работы (i, j)), которое находится в пределах ранних сроков начала непосредственно следующих и поздних сроков окончания непосредственно предшествующих работ (рис. 11):

- , если i = 1,

= - - , если 1 < i < m,

- - , если j = m

1)

, i = 1, j < m,

2 )

0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 , 1<i<m, 1<j<m,

3 ) , , 1<i ≤(m-1), j = m.

Рис. 11. Графическая интерпретация расчета

свободного резерва времени работы (i, j)

Общие выводы:

1. Полный и частные резервы работы (i, j) будут равны, если конечное событие этой работы j является событием, лежащим на критическом пути.

2. Между полным резервом и частным резервом времени второго вида всегда имеет место соотношение:

.

3. Если конечное событие (j) какой-либо работы (i, j) принадлежит критическому пути, то полный и частные резервы (первого и второго вида) будут равны.

4. Если полный резерв некоторой работы равен нулю, то и частный резерв второго вида также равен нулю.

5. Полный и частные резервы времени всегда являются положительным числом, то есть они больше или равны нулю.

6. Чтобы частный резерв времени работы (i, j) был равен нулю, необходимо и достаточно, чтобы эта работа лежала на пути максимальной длины от исходного события до события j. При этом событие j может быть как промежуточным, так и завершающим.

Далее представлена принципиальная схема расчетов параметров сетевого графа (в терминах работ), регламентирующая последовательность всех расчетов параметров графа (рис.12).

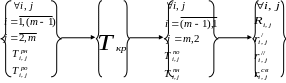
Рис.12. Принципиальная схема последовательности

выполнения расчетов параметров сетевого графа