
- •Вивчення властивостей еліпса за канонічним рівнянням
- •Знайти рівняння множини точок площини для кожної з яких сума відстаней до і рівна 12.
- •Знайти рівняння множини точок площини для кожної з яких сума відстаней до і рівна 15.
- •Знайти точки перетину прямої з еліпсом .
- •Вивчення властивостей гіперболи за канонічними рівнянням.
- •Знайти точки перетину прямої і гіперболи .
- •Ексцентриситет дорівнює ;
- •Вибравши на площині прямокутну декартову систему координат, зобразіть область задану наступними системами:
- •Вивчення властивостей параболи за канонічним рівнянням
Вивчення властивостей параболи за канонічним рівнянням
Визначити координати фокуса
 і скласти рівняння директриси для
кожної з наступних
парабол: а)
і скласти рівняння директриси для
кожної з наступних
парабол: а) ; b)
; b) ; c)
; c)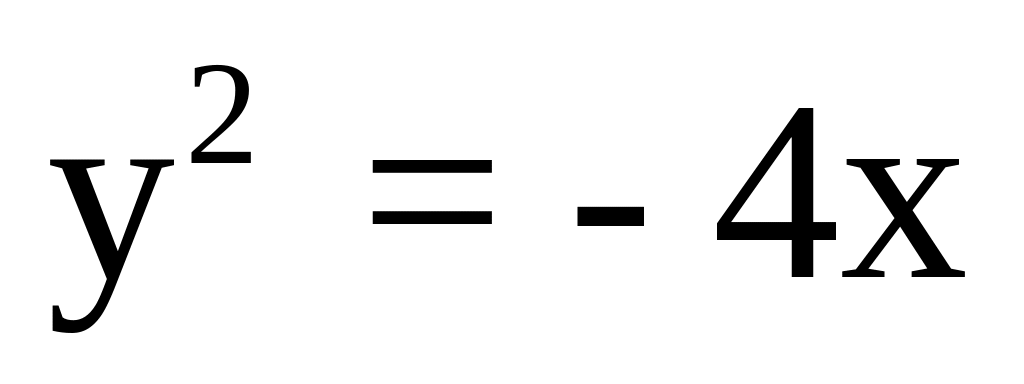 ; d)
; d) ; e)
; e)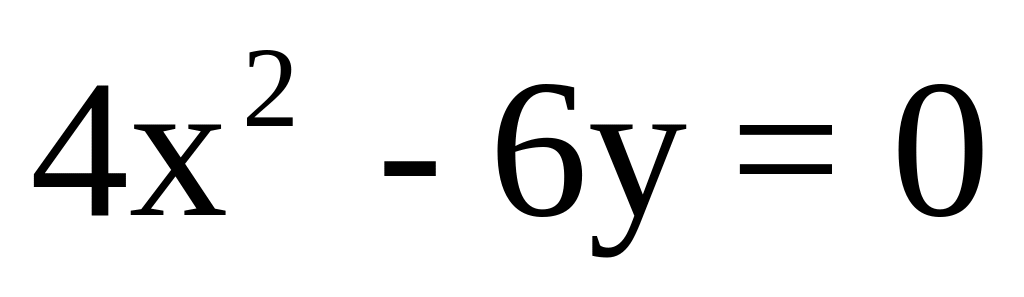 ; f)
; f)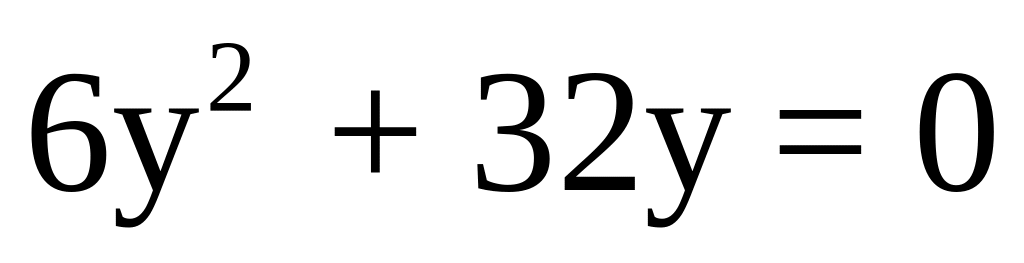 ;
;Скласти канонічне рівняння параболи в кожному з таких випадків:
a) відстань від фокуса, що лежить на осі Ох, до вершини дорівнює 4;
b) парабола симетрична відносно осі абсцис і проходить через точку M (1, 2);
c) парабола
симетрична відносно осі
![]() абсцис
і проходить через точку M (1, 2);
абсцис
і проходить через точку M (1, 2);
Скласти канонічне рівняння параболи в кожному з наступних випадків: а) фокус має координати
 ;
b)
фокус має координати
;
b)
фокус має координати
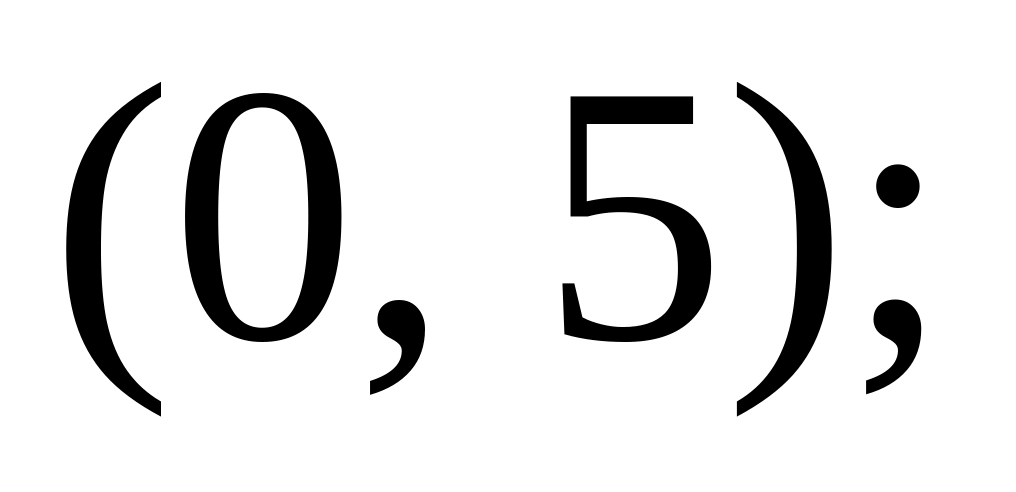 c)
директриса має рівняння
c)
директриса має рівняння
 ;
d) директриса має
рівняння
;
d) директриса має
рівняння
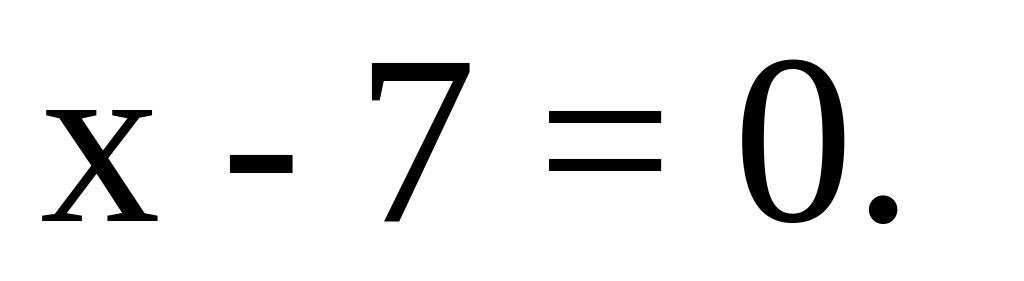
Обчислити фокальний радіус
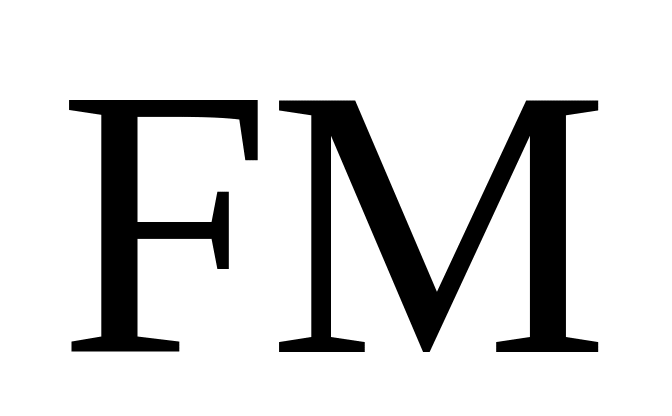 точки
параболи
точки
параболи ,
якщо її абсциса дорівнює
,
якщо її абсциса дорівнює .
Тут
.
Тут
 –
фокус параболи.
–
фокус параболи.Побудуйте лінію в прямокутній декартовій системі координат:
a)![]() ;
;
b)![]() ;
;
c) .
На параболі
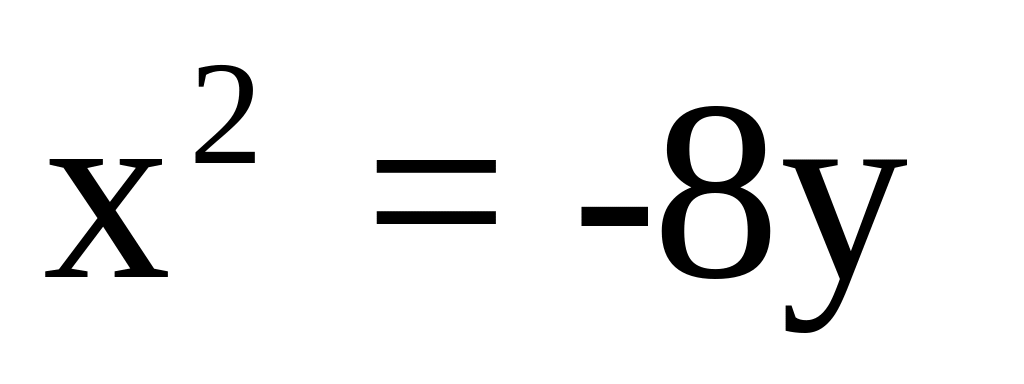 знайти
точку, фокальний радіус якої дорівнює
7.
знайти
точку, фокальний радіус якої дорівнює
7.Під гострим кутом до горизонту кинуто камінь, який, рухаючись по параболі, упав на відстані 12 м. від початкового положення. Визначити параметр траєкторії, знаючи, що найбільша висота, досягнута каменем, дорівнює 3 м.
Визначити площу неорієнтованого трикутника, у якого одна вершина, належить директрисі параболи
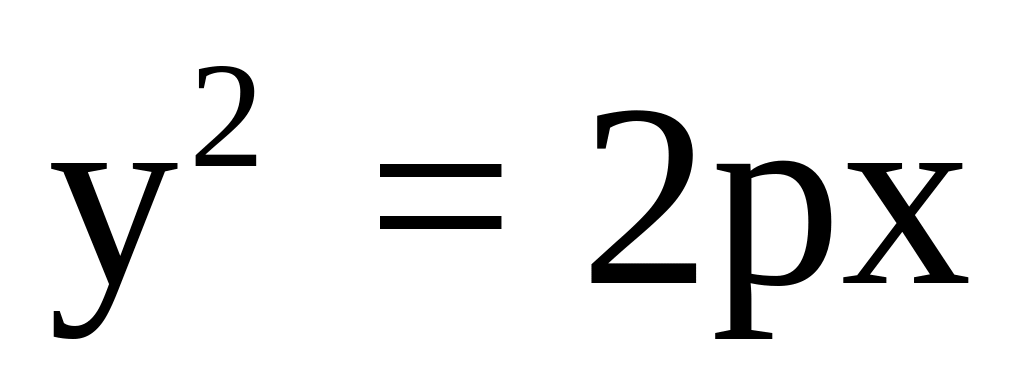 ,
а дві інші служать кінцями хорди, що
проходять через фокус і перпендикулярна
до осі
,
а дві інші служать кінцями хорди, що
проходять через фокус і перпендикулярна
до осі

Обчислити довжину сторони правильного трикутника
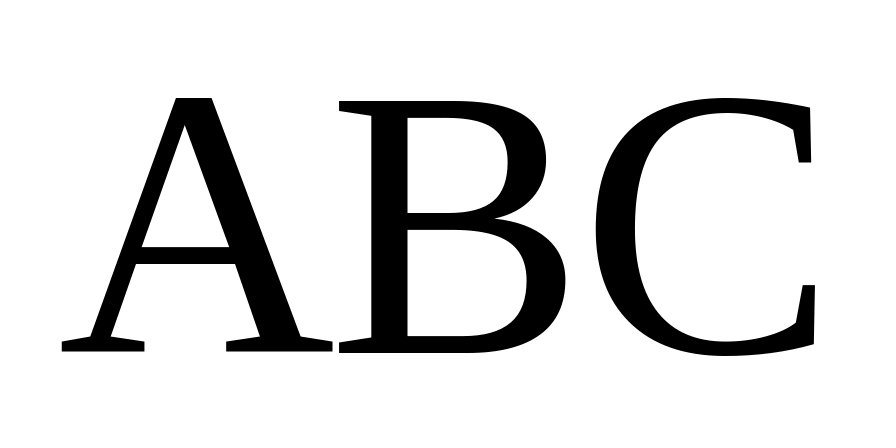 ,
вписаного в параболу з параметром
,
вписаного в параболу з параметром
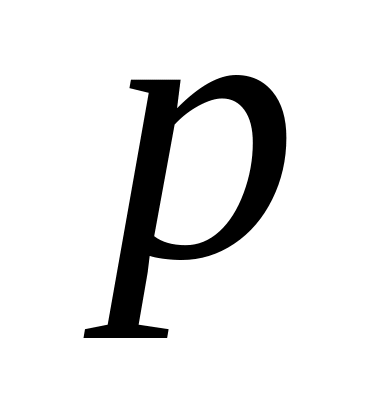 ,
якщо припустити, що точка
,
якщо припустити, що точка
 збігається з вершиною параболи.
збігається з вершиною параболи.Знайти довжини сторін трикутника, вписаного в параболу з параметром , якщо одна вершина збігається з вершиною параболи, а ортоцентр – з фокусом.
В кожному з наступних випадків скласти канонічне рівняння параболи, заданої в полярній системі координат:
![]() і
і ![]() .
Передбачається, що за полюс прийнятий
фокус параболи, а за полярну вісь - вісь
симетрії, спрямована від директриси до
фокусу.
.
Передбачається, що за полюс прийнятий
фокус параболи, а за полярну вісь - вісь
симетрії, спрямована від директриси до
фокусу.
Написати рівняння парабол:
а) ;
б)![]() ;
;
в полярній системі координат, якщо полюс збігається з фокусом параболи, а полярна вісь - з віссю .
Написати рівняння прямої, що проходить через точку
 ,
на якій парабола
відсікає
хорду, серединою якої служить точка
,
на якій парабола
відсікає
хорду, серединою якої служить точка
 .
.Довести: якщо пряма
 не
паралельна осі
не
паралельна осі ,
то, для того щоб вона була дотичною до
параболи
,
то, для того щоб вона була дотичною до
параболи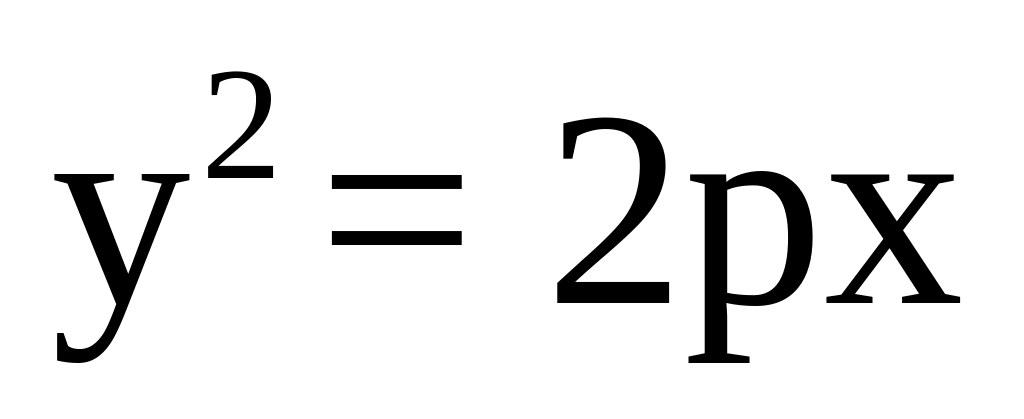 ,
необхідно та достатньо, щоб
,
необхідно та достатньо, щоб

Скласти рівняння дотичної до параболи
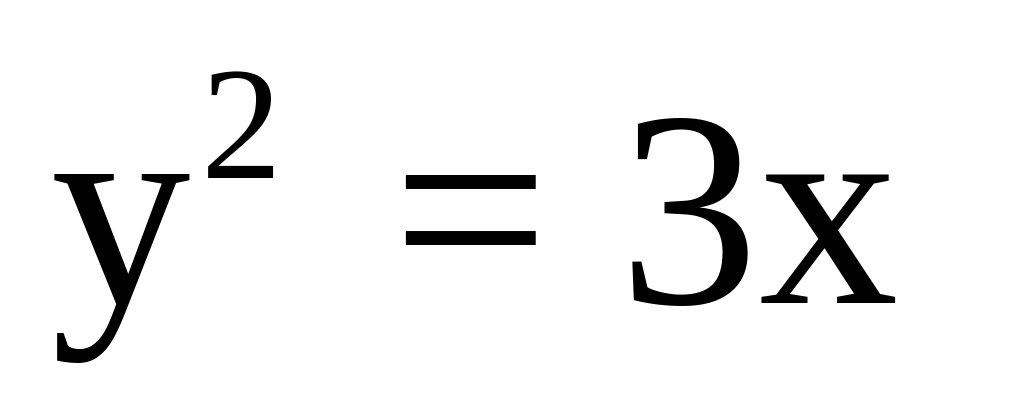 в
точці
в
точці
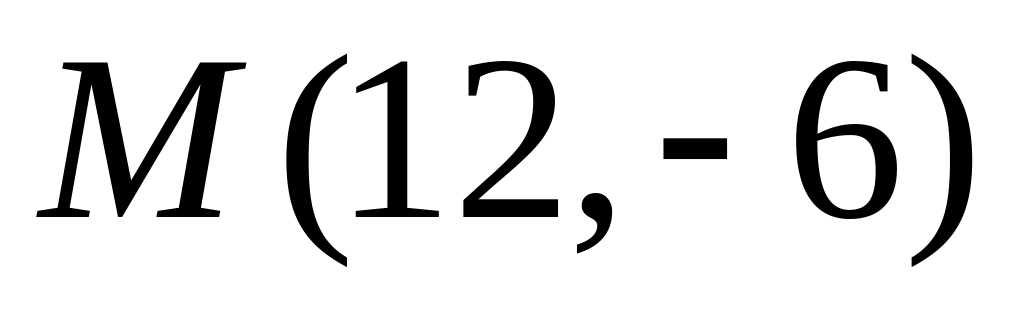 .
.Написати рівняння прямої, що має кутовий коефіцієнт k ≠ 0 і дотикається до параболи .
Написати рівняння прямих
 і
і
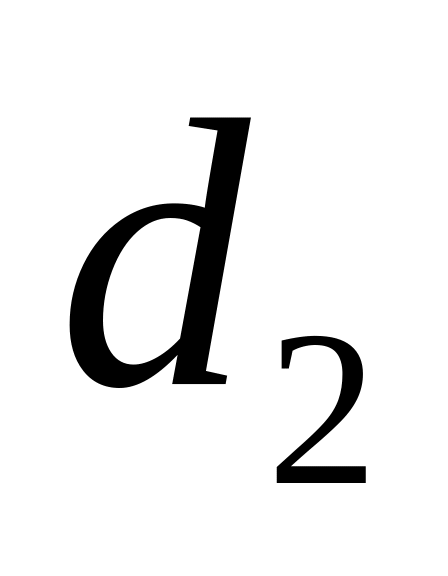 ,
які мають кутові коефіцієнти
,
які мають кутові коефіцієнти
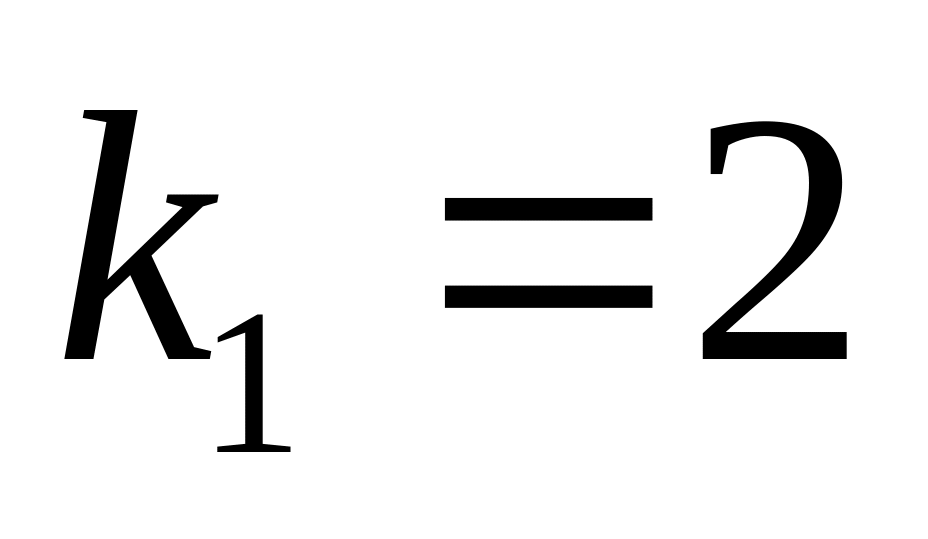 і
і
 відповідно і дотичні до параболи
відповідно і дотичні до параболи
 .
.Взявши на площині прямокутну декартову систему координат, побудувати області, які визначаються наступними системами нерівностей:
a)
![]()
 b)
b)
Знайти найкоротшу відстань від точок параболи
 до прямої
до прямої
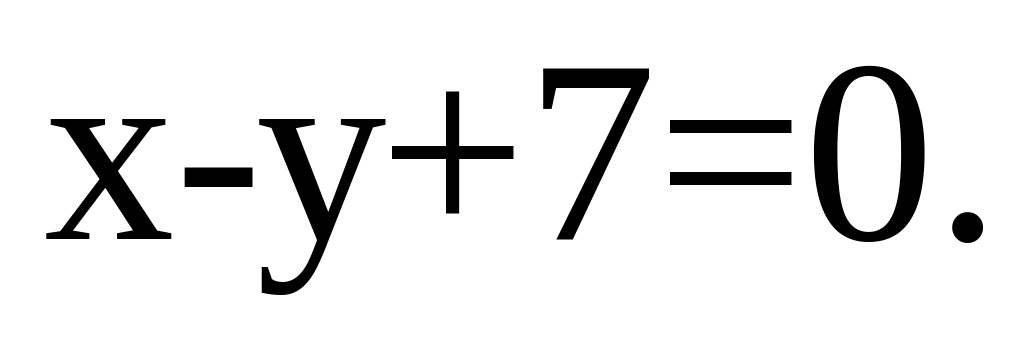
Знайти множину основ перпендикулярів, опущених з фокуса параболи на всі її дотичні.
Знайти множину всіх точок, кожна з яких симетрична фокусу F параболи відносно деякої дотичної.
Знайти множину точок, з яких параболу у2 = 2рх видно під прямим кутом.
Якщо з будь-якої точки директриси проведені до параболи дві дотичні, то пряма, що з'єднує точки дотику, проходить через фокус параболи. Довести.
Довести оптичну властивість параболи: всяка дотична до параболи утворює рівні кути з фокальним радіусом точки і з променем, що проходить через точку дотику і співнапрямлена з віссю.
Довести, що добуток довжин перпендикулярів, опущених з кінців будь-якої, фокальної хорди (тобто хорди, що проходить через фокус) на вісь параболи, має постійну величину
Деякі поверхні другого порядку. Їхні канонічні рівняння, властивості та зображення.
Поверхні обертання.
Напишіть рівняння сфери з центром в точці
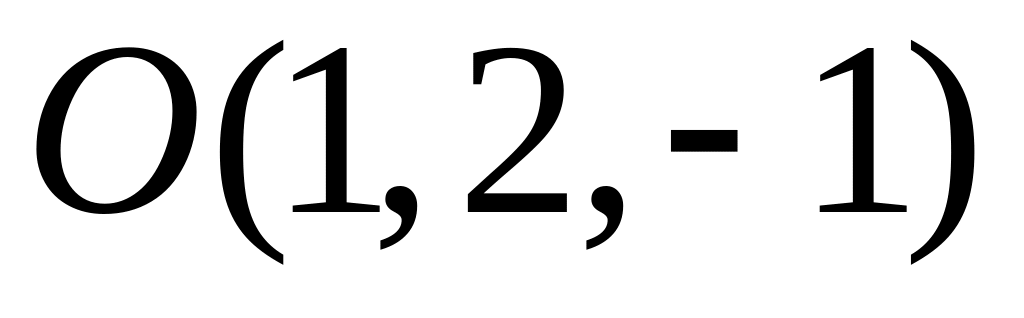 і
радіусом
і
радіусом
 .
.Напишіть рівняння сфери з центром в точці
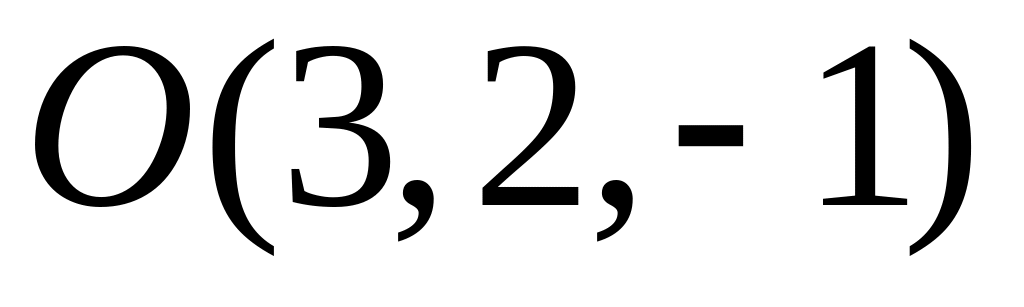 яка проходить через точку
яка проходить через точку
 .
.Складіть рівняння сфери, яка проходить через точку
 і дотикається площини
і дотикається площини
 в точці
в точці
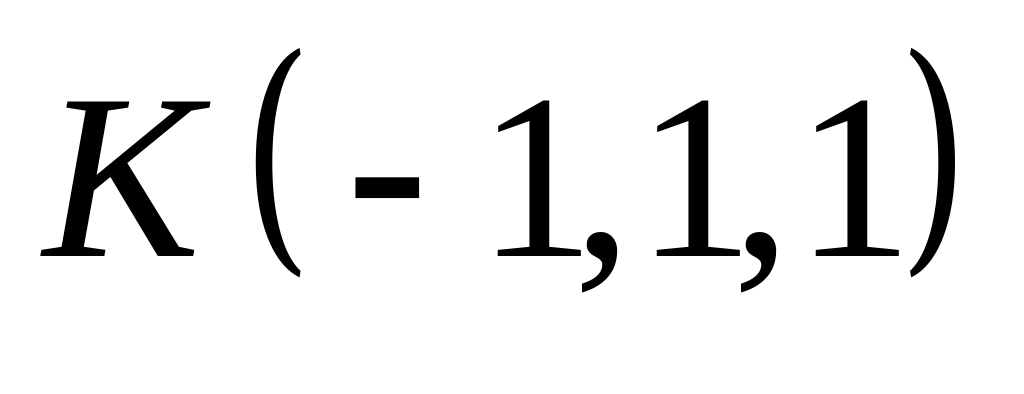 .
.Складіть рівняння кола, з діаметром
 ,
яке проходить через точку
,
яке проходить через точку
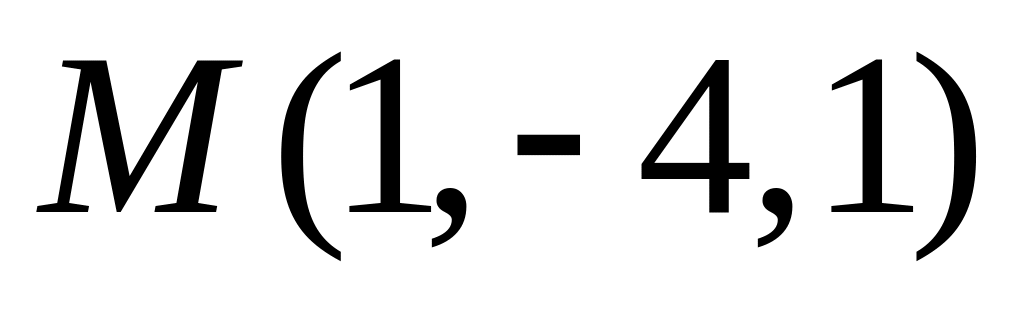 .
Якщо відомі координати точок
.
Якщо відомі координати точок
 і
і
 .
.Складіть рівняння сфери, якщо відомо, що вона проходить через точки
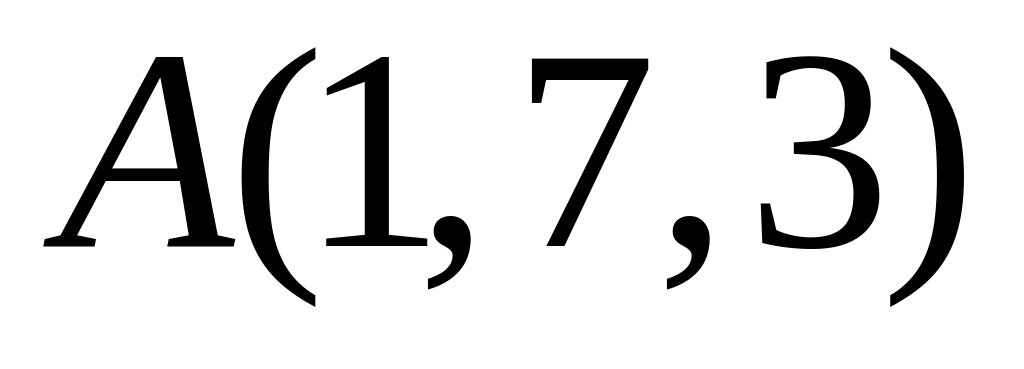 ,
,
 ,
,
 ,
,
 .
.Визначте координати центра і довжину радіуса для кожної з наступних сфер:
 ,
,
 ,
,
 .
.
В площині
 задано
коло з центром в точці
задано
коло з центром в точці
 і радіусом 3. Запишіть рівняння поверхні,
яка утвориться в наслідок обертання
даного кола навколо осі 1)
і радіусом 3. Запишіть рівняння поверхні,
яка утвориться в наслідок обертання
даного кола навколо осі 1) ,
2)
,
2) .
.Коло радіуса
 розташоване в площині
так,
що дотикається осі
в початку координат. Запишіть рівняння
поверхні, яка утвориться в наслідок
обертання даного кола навколо осі
.
розташоване в площині
так,
що дотикається осі
в початку координат. Запишіть рівняння
поверхні, яка утвориться в наслідок
обертання даного кола навколо осі
.Знайдіть точки перетину прямої з поверхнею:
 .
.
Знайдіть точки перетину прямої з поверхнею:
 .
.Скласти рівняння поверхні утвореної внаслідок обертання параболи
 навколо осі
.
навколо осі
.Парабола з параметром 6 розміщена на площині так, що директриса співпадає з віссю . Запишіть рівняння поверхні, яка утвориться в наслідок обертання даної лінії навколо осі .
Скласти рівняння поверхонь, які утворяться внаслідок обертання навколо осі
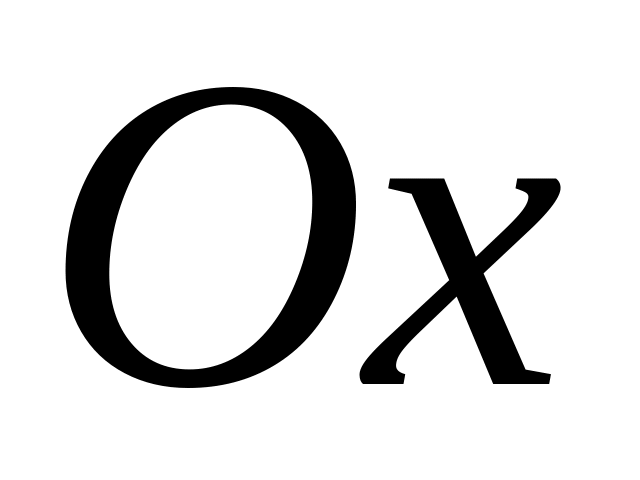 кожної
з наступних ліній:
кожної
з наступних ліній:Еліпса
 .
. Гіперболи
 .
.Гіперболи
 .
.Параболи
 .
.
Запишіть рівняння поверхні, яка утвориться внаслідок обертання синусоїди
 навколо осі 1)
; 2)
.
навколо осі 1)
; 2)
.
Дослідити методом перерізів наступні поверхні, задані в прямокутній декартовій системі координат:
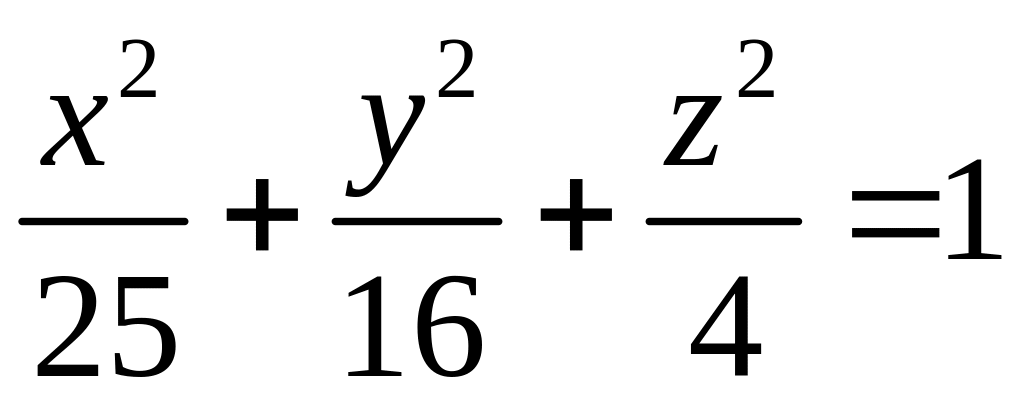 ;
; ;
; ;
;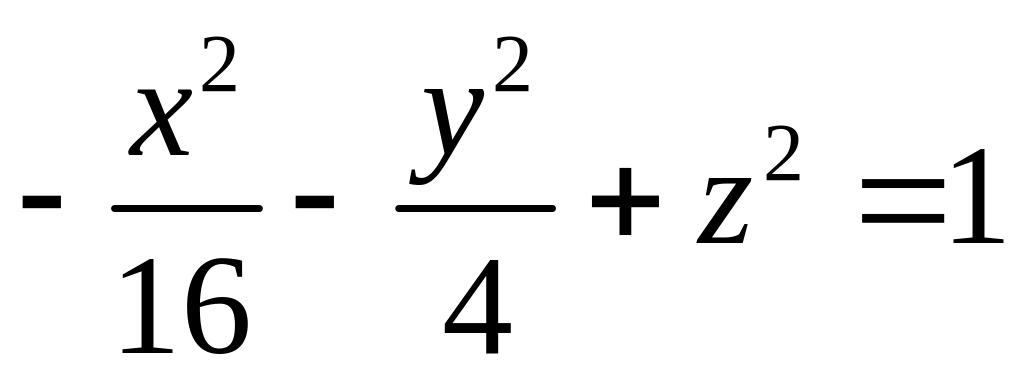 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;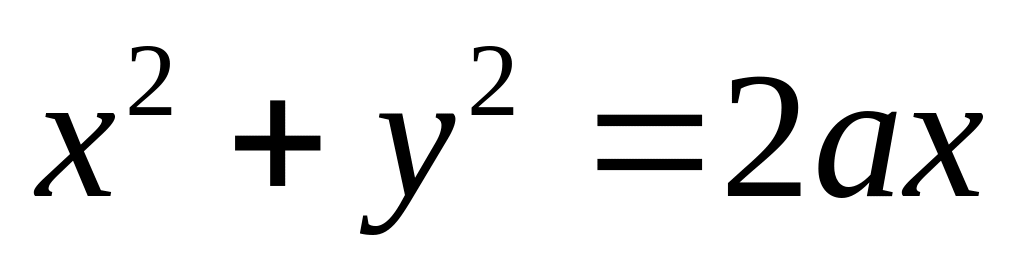 .
.
Вказати взаємне розміщення еліпсоїда
 і площини
і площини
 в залежності від значень параметра
в залежності від значень параметра
 .
.Зобразити тіло обмежене поверхнями:
Циліндричні та конічні поверхні.
Пряма
 розташована в площині
розташована в площині
 обертається
навколо осі
обертається
навколо осі
 .
Скласти рівняння поверхні що утворилась.
.
Скласти рівняння поверхні що утворилась.Скласти рівняння циліндра напрямною якого є лінія
 ,
а твірна паралельна вектору
,
а твірна паралельна вектору
 .
.Скласти рівняння циліндра напрямною якого є лінія
 а твірна паралельна
а твірна паралельна
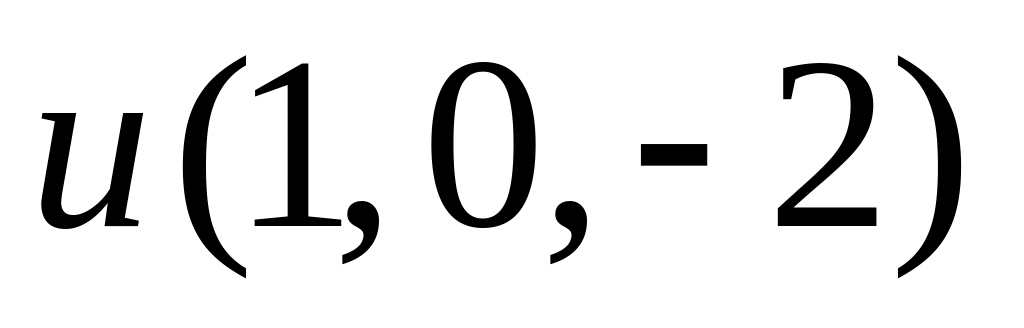 .
.Скласти рівняння кругового циліндра, якщо відомо рівняння його осі
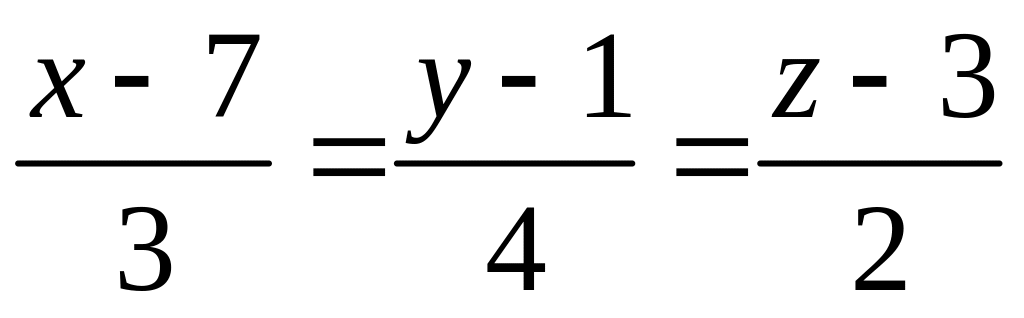 і координати точки
і координати точки
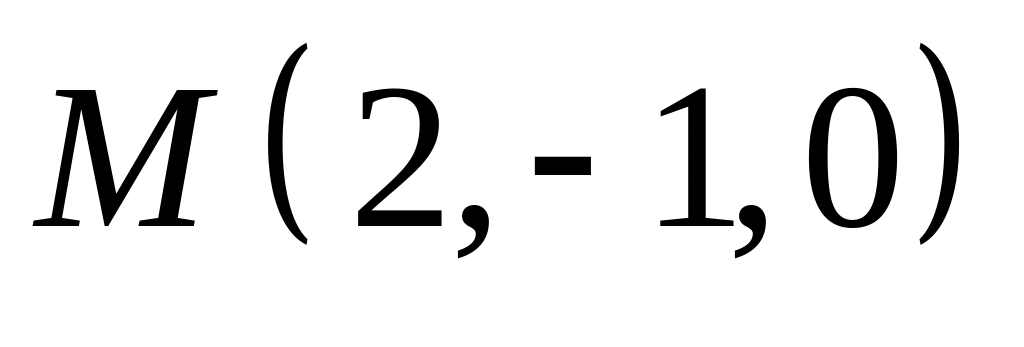 ,
розташованої на поверхні циліндра.
,
розташованої на поверхні циліндра.Скласти рівняння циліндра напрямною якого є лінія
 а твірна паралельна
а твірна паралельна
 .
.Скласти рівняння поверхні, що утворюється обертанням навколо осі прямої
 .
.Скласти рівняння поверхні, що утворюється обертанням навколо осі прямої
 .
.Скласти рівняння поверхні, що утворюється внаслідок обертання прямої
 навколо осі
.
навколо осі
.Знайдіть рівняння конуса напрямною якого є лінія
 а вершина розташована в точці
а вершина розташована в точці
 .
.Знайдіть рівняння конуса напрямною якого є лінія
 а вершина розташована в точці
а вершина розташована в точці
 .
.Скласти рівняння конуса, який проектує еліпс
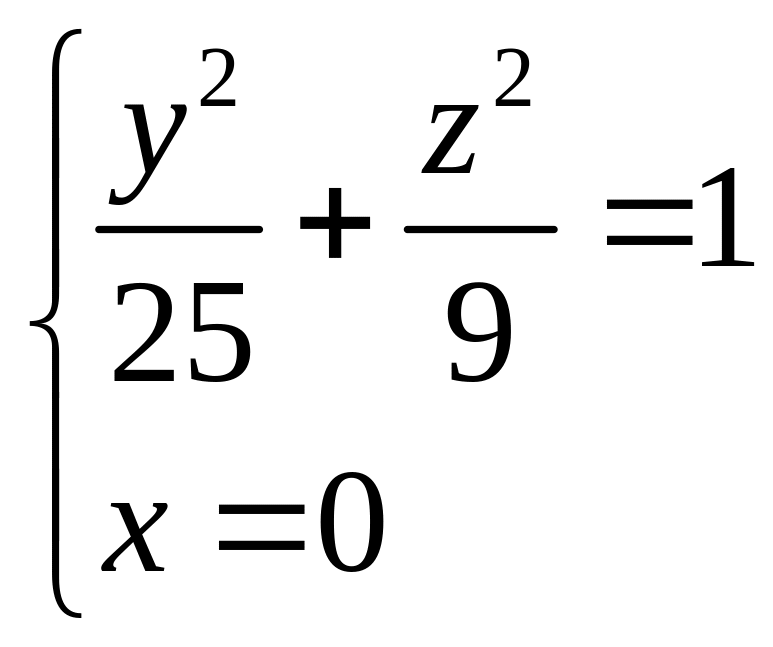 з точки
з точки
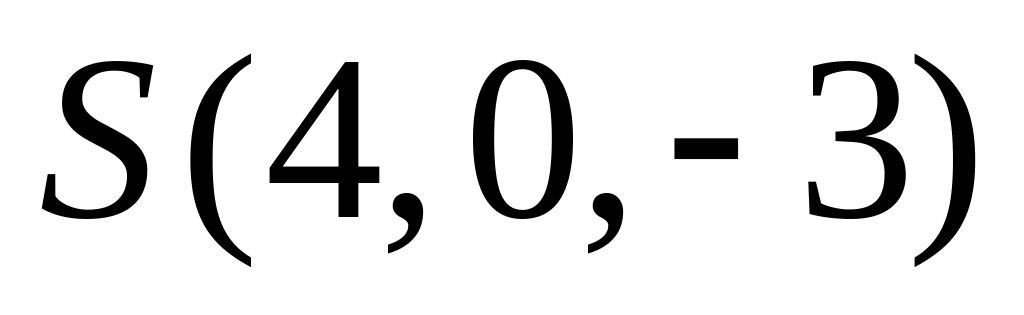 .
.Скласти рівняння конуса з вершиною в точці
 ,
твірні якої утворюють з площиною
,
твірні якої утворюють з площиною
 кут
кут
 .
.Скласти рівняння конуса з вершиною в точці
 описаного навколо параболоїда
описаного навколо параболоїда
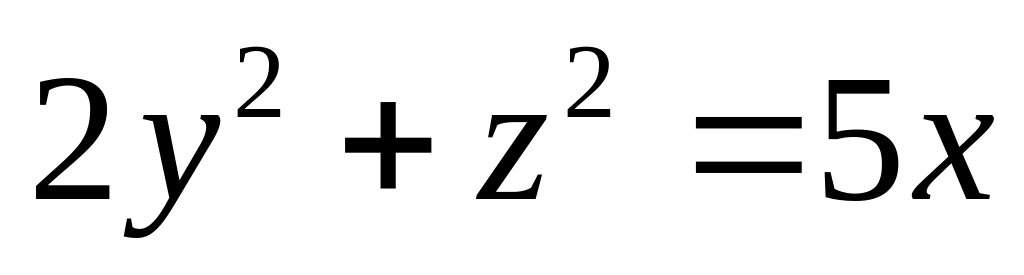 .
.Знайти рівняння твірних циліндра
 ,
які проходять через точку
,
які проходять через точку
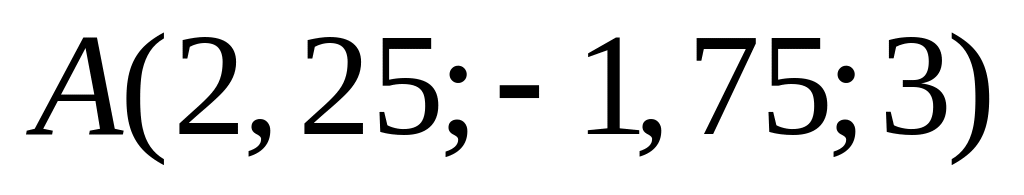 .
.Знайти рівняння твірних конуса
 .
.Знайти рівняння твірних гіперболоїда
 ,
які проходять через точку
,
які проходять через точку
 .
.Визначте кут між твірною конуса і його віссю
 .
.



