
- •Вивчення властивостей еліпса за канонічним рівнянням
- •Знайти рівняння множини точок площини для кожної з яких сума відстаней до і рівна 12.
- •Знайти рівняння множини точок площини для кожної з яких сума відстаней до і рівна 15.
- •Знайти точки перетину прямої з еліпсом .
- •Вивчення властивостей гіперболи за канонічними рівнянням.
- •Знайти точки перетину прямої і гіперболи .
- •Ексцентриситет дорівнює ;
- •Вибравши на площині прямокутну декартову систему координат, зобразіть область задану наступними системами:
- •Вивчення властивостей параболи за канонічним рівнянням
Вивчення властивостей еліпса за канонічним рівнянням
Знайти рівняння множини точок площини для кожної з яких сума відстаней до
 і
і
 рівна 8.
рівна 8.Знайти рівняння множини точок площини для кожної з яких сума відстаней до і рівна 12.
Знайти рівняння множини точок площини для кожної з яких сума відстаней до і рівна 15.
Задано еліпс, в якого відстані від правого фокуса до кінців великої осі відповідно дорівнюють 1 і 7. Скласти рівняння еліпса.
Довжина великої осі еліпса 8 ексцентриситет еліпса
 ,
відстань від деякої точки
,
відстань від деякої точки
 еліпса
до його правого фокуса 3. Знайдіть
координати точки
,
відстань від
до лівого фокуса, канонічне рівняння
еліпса.
еліпса
до його правого фокуса 3. Знайдіть
координати точки
,
відстань від
до лівого фокуса, канонічне рівняння
еліпса.Побудуйте лінію в прямокутній декартовій системі координат, знайдіть її центр, ексцентриситет, фокуси :
 .
.
В кожному з наступних випадків знайдіть канонічне рівняння еліпса: 1)

 ;
2)
;
2)
 і
і
 3)
3)
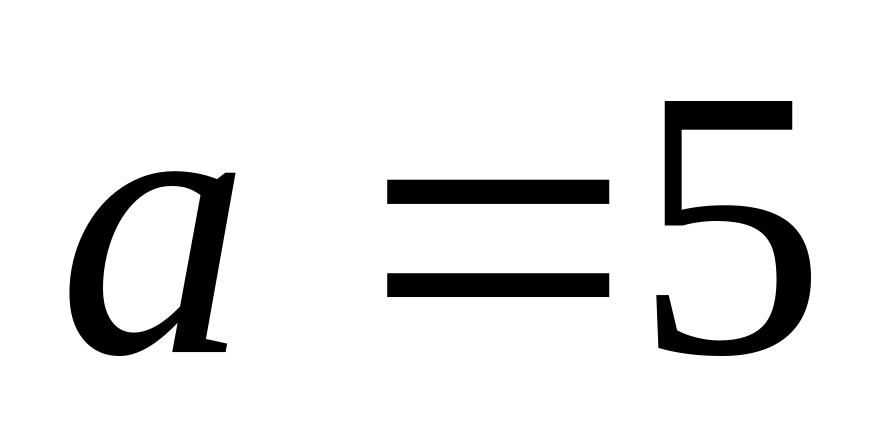 і
і
 .
.Знайти довжини півосей, координати вершин, фокусів, ексцентриситет, зобразити лінію в декартовій системі координат: 1)
 .
2)
.
2)
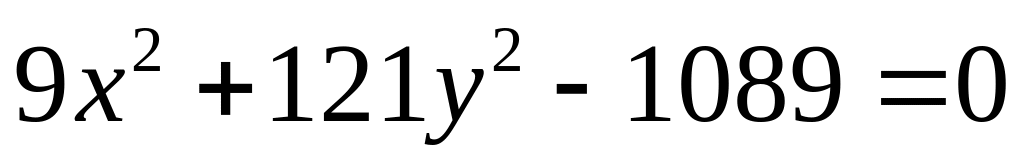 .
3)
.
3)
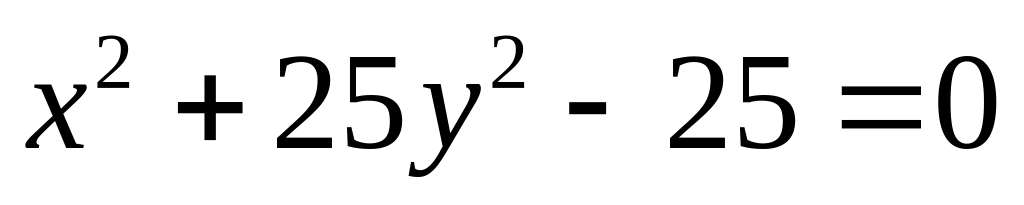 .
4)
.
4)
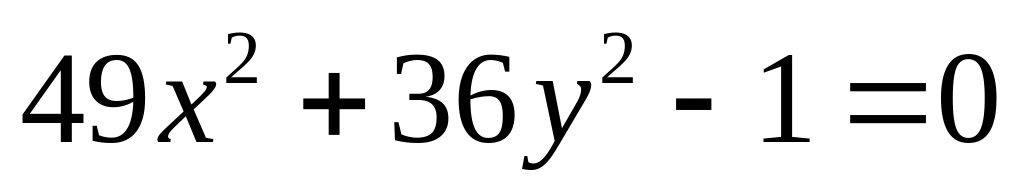 .
.Через фокус
 проведена
хорда еліпса
проведена
хорда еліпса
 паралельно канонічній осі
паралельно канонічній осі
 .
Знайдіть довжину цієї хорди.
.
Знайдіть довжину цієї хорди.На еліпсі
 знайти точку фокусні радіус-вектори
якої взаємно перпендикулярні.
знайти точку фокусні радіус-вектори
якої взаємно перпендикулярні.Хорда проведена через фокус паралельно канонічній осі перетинає еліпс
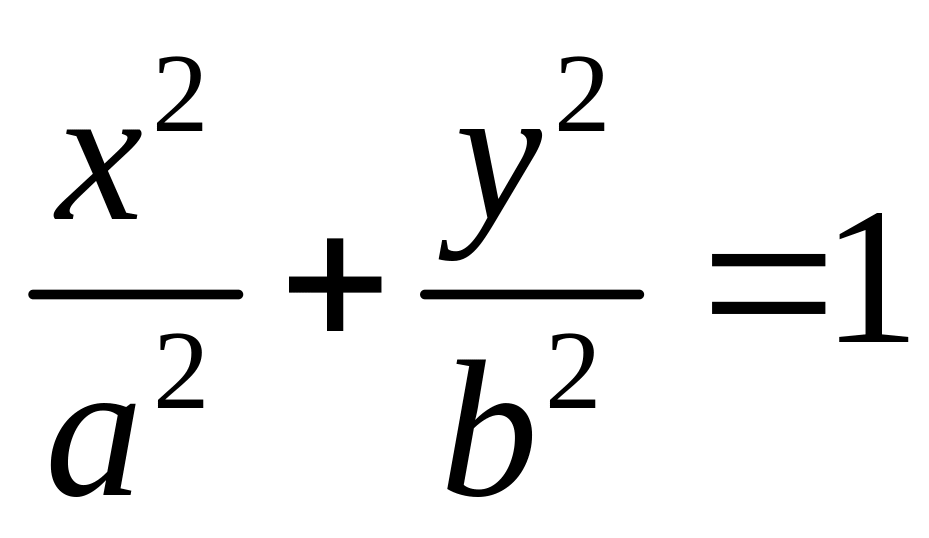 в точках
в точках
 і
і
 .
Знайдіть відстань від.
і
.до
.
Знайдіть відстань від.
і
.до
 .
.Знайти канонічне рівняння еліпса, фокусами якого є точки
 та
та
 ,
а велика піввісь
.
,
а велика піввісь
.Написати канонічне рівняння еліпса, якщо:
задано вершини еліпса
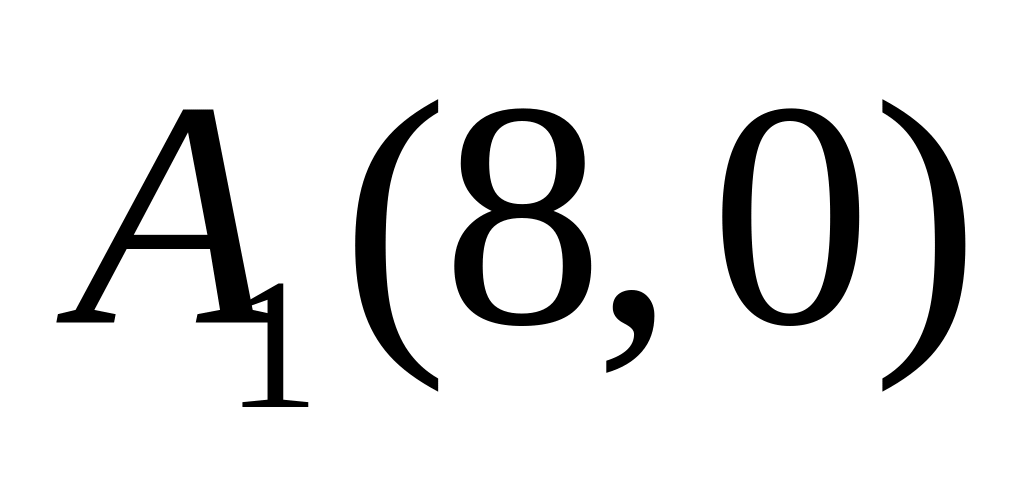 ,
,
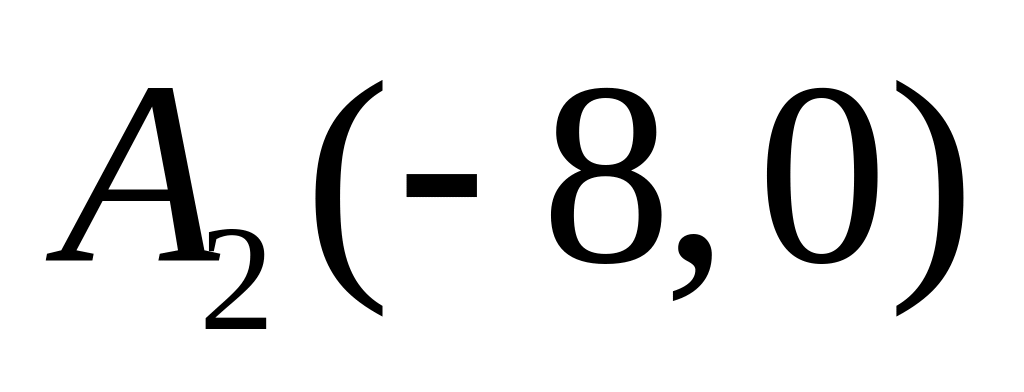 ,
,
 і
і
 ;
;відстань між фокусами дорівнює 8, а ексцентриситет
 ;
;велика вісь дорівнює 26, а ексцентриситет
 ;
;відстань між фокусами 8, а велика вісь дорівнює 12.
Скласти рівняння еліпса в канонічній системі координат, якщо:
еліпс проходить через точку
 і відстань між фокусами дорівнює 6;
і відстань між фокусами дорівнює 6;еліпс проходить через точку
 і має ексцентриситет
і має ексцентриситет
 ;
;еліпс проходить через точку
 і його мала піввісь дорівнює 3.
і його мала піввісь дорівнює 3.
Задано еліпс
 .
Знайти рівняння директрис.
.
Знайти рівняння директрис.Знайти відстань між директрисами еліпса
 .
.Скласти канонічне рівняння еліпса, якщо:
прямі
 – його директриси, а мала піввісь
дорівнює 2;
– його директриси, а мала піввісь
дорівнює 2;відстань між директрисами
 ,
а між фокусами
,
а між фокусами
 ;
;відстань між директрисами
 ,
а ексцентриситет
,
а ексцентриситет
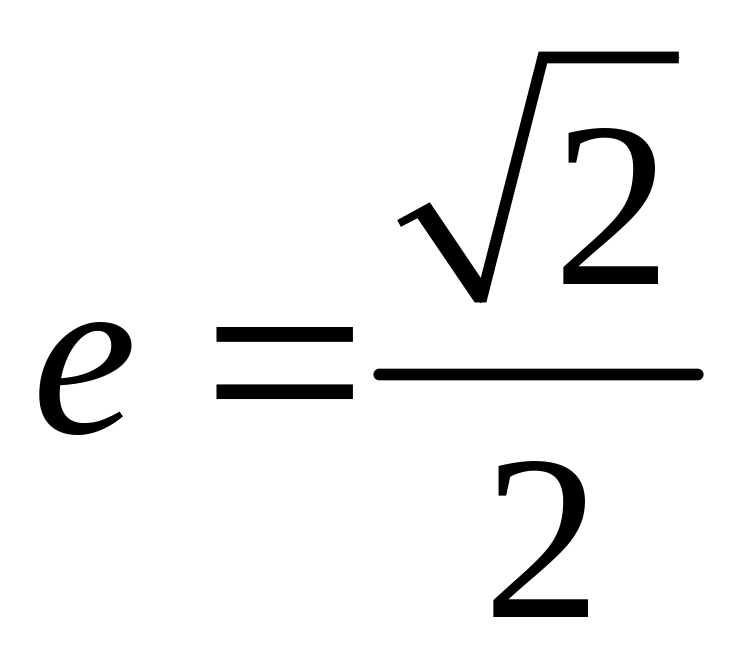 .
.
Ексцентриситет еліпса
 ,
відстань від точки
еліпса до директриси дорівнює 12. Знайти
відстань від
до відповідного фокуса.
,
відстань від точки
еліпса до директриси дорівнює 12. Знайти
відстань від
до відповідного фокуса.Скласти рівняння дотичної до еліпса
 в точці
в точці
 .
.Скласти рівняння тих дотичних до еліпса
 ,
які паралельні прямій
,
які паралельні прямій
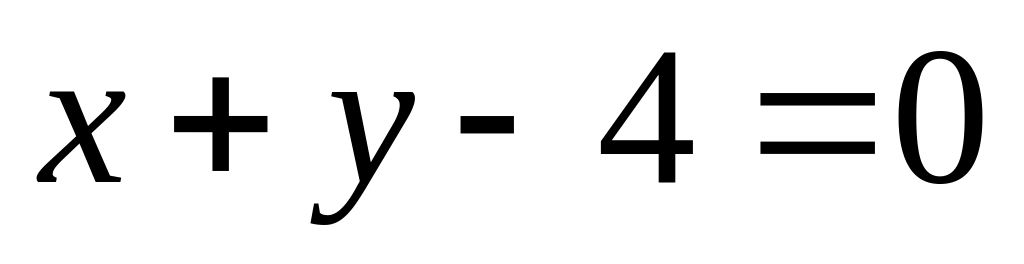 .
.Знайти точки перетину прямої
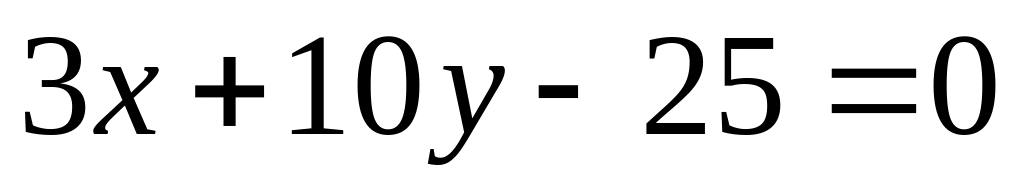 з
еліпсом
з
еліпсом
 .
.Знайти точки перетину прямої з еліпсом .
Визначити взаємне розміщення прямої і еліпса:
 і
і
 ;
;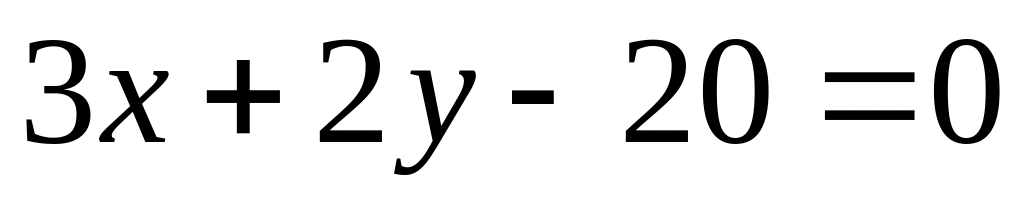 і
і
 ;
; і
і
 .
.
Провести до еліпса
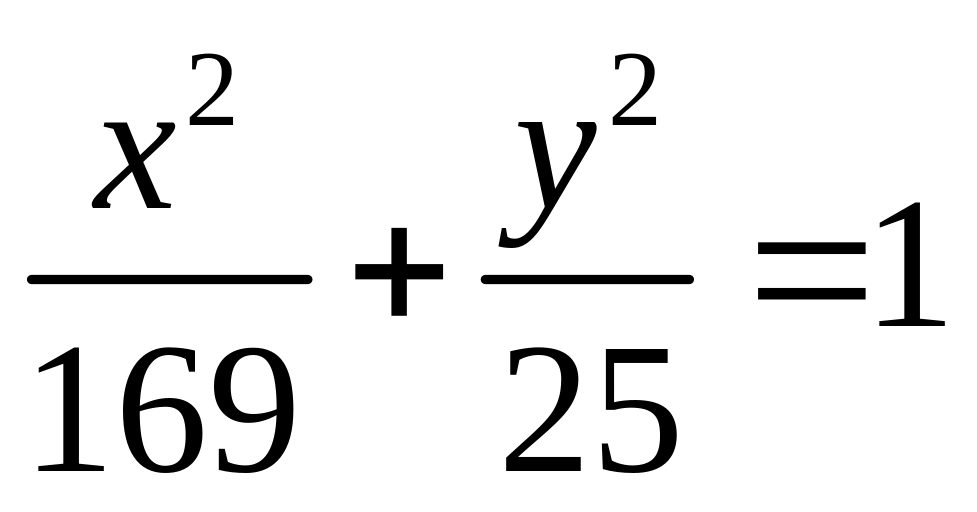 дотичні, перпендикулярні прямій
дотичні, перпендикулярні прямій
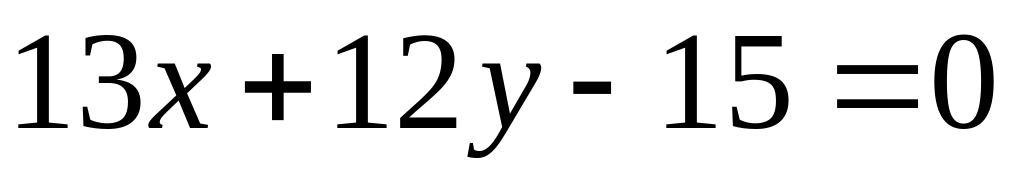 .
.Вибравши на площині прямокутну декартову систему координат, зобразіть область задану наступними системами:
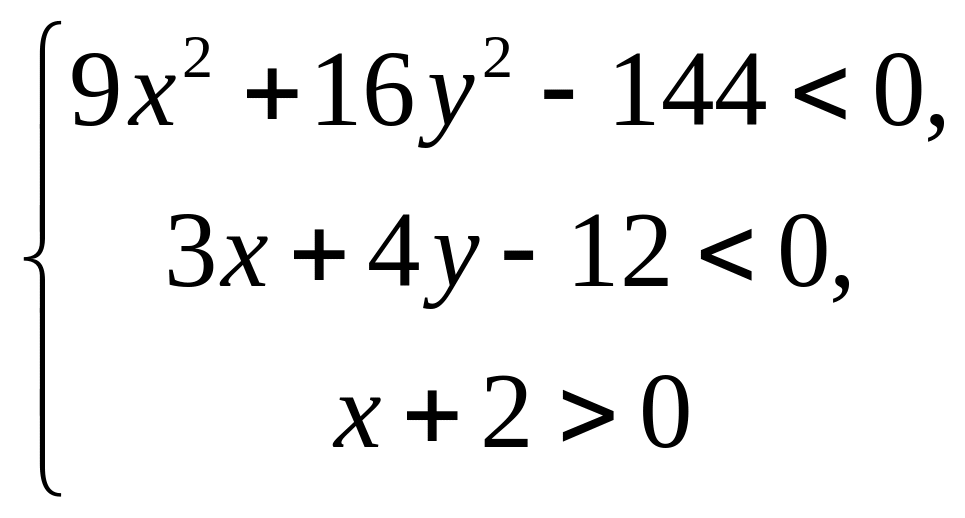
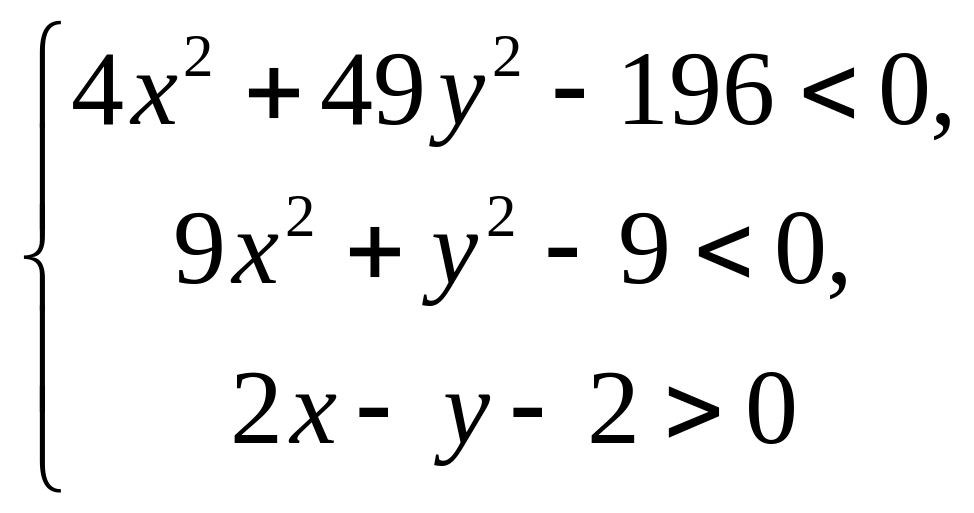
Скласти рівняння дотичних до еліпса
 ,
які проходять через точку
,
які проходять через точку
 .
.Знайти рівняння прямої яка проходить через точку
 ,
на якій еліпс
,
на якій еліпс
 відтинає хорду, яка точкою
ділиться навпіл.
відтинає хорду, яка точкою
ділиться навпіл.Доведіть, що відрізок дотичної до еліпса, розташований між дотичними, проведеними в вершинах, які лежать на великій осі, видно з фокусів еліпса під прямим кутом.
Доведіть, що добуток відстаней від фокусів до довільної дотичної до еліпса є величина стала і дорівнює квадрату малої півосі.
Обчисліть довжини півосей і відстань між фокусами еліпса, заданого в полярній системі координат рівнянням
 .
Вважаємо, що за полюс прийнято фокус
,
а за полярну вісь – направлену пряму
.
Вважаємо, що за полюс прийнято фокус
,
а за полярну вісь – направлену пряму
 ,
де
– інший фокус еліпса.
,
де
– інший фокус еліпса.Знайдіть канонічні рівняння еліпсів, заданих в полярній системі координат рівняннями:
 ,
,
 .
.Знайдіть рівняння еліпсів
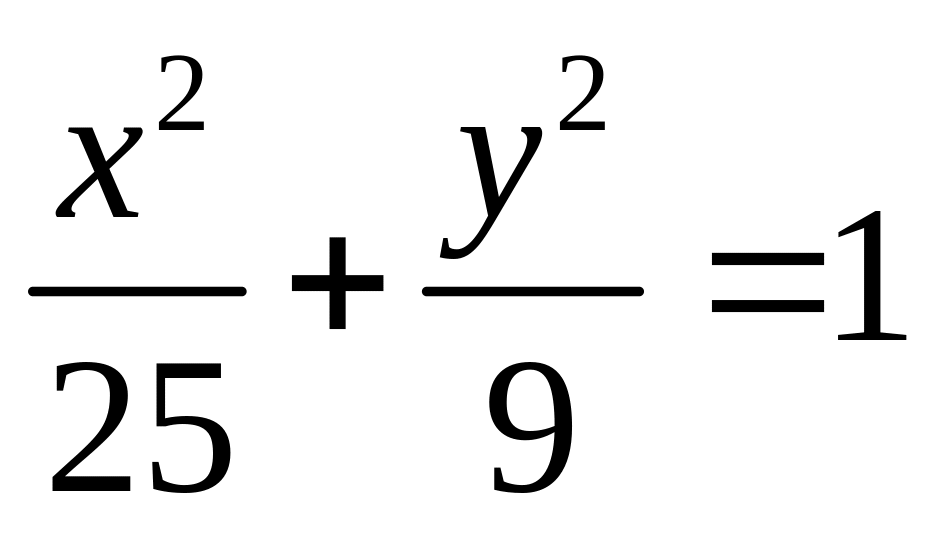 і
і
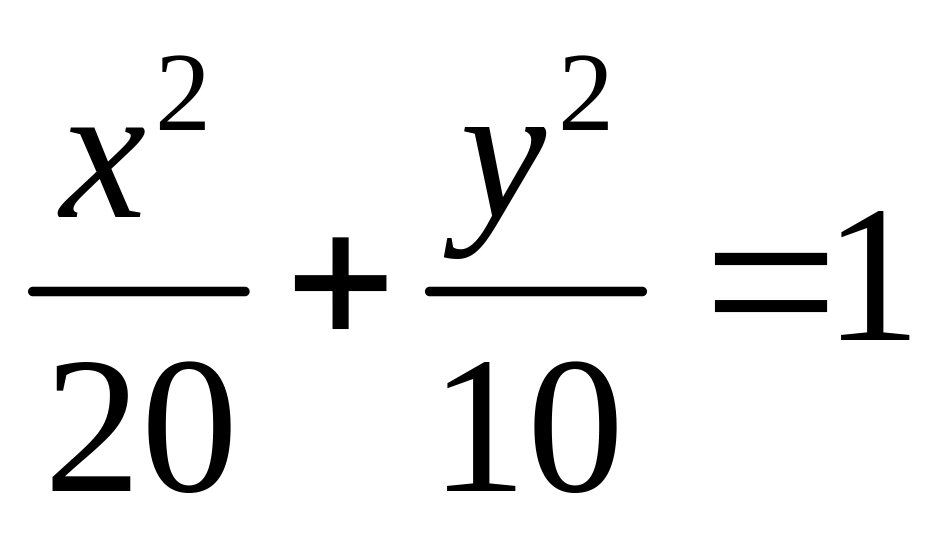 , в полярній системі координат, якщо
полюс розміщено в фокусі
,
а за полярну вісь прийнято направлену
пряму
,
де
– інший фокус еліпса.
, в полярній системі координат, якщо
полюс розміщено в фокусі
,
а за полярну вісь прийнято направлену
пряму
,
де
– інший фокус еліпса.
