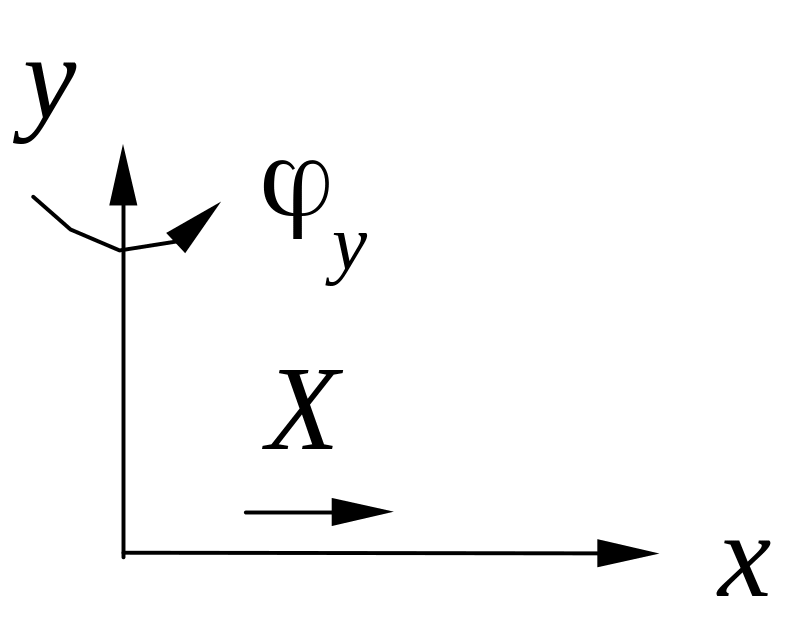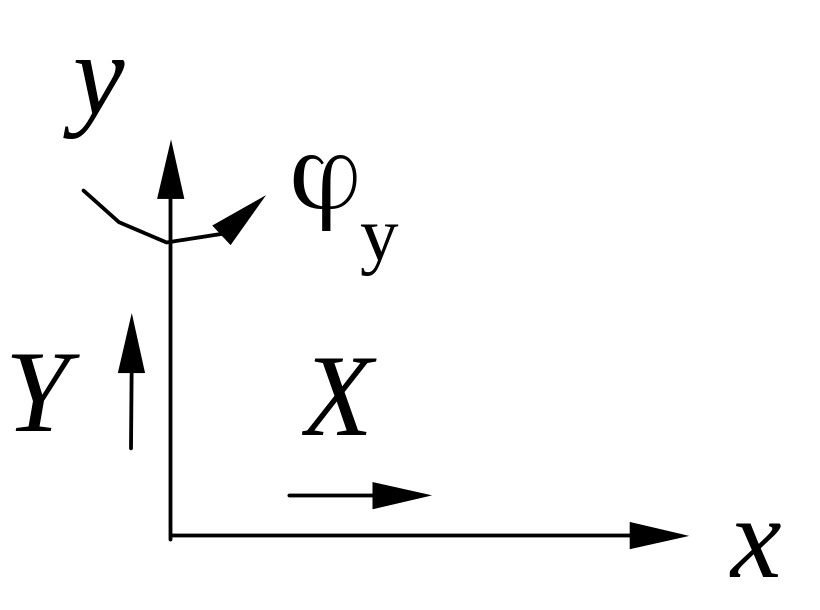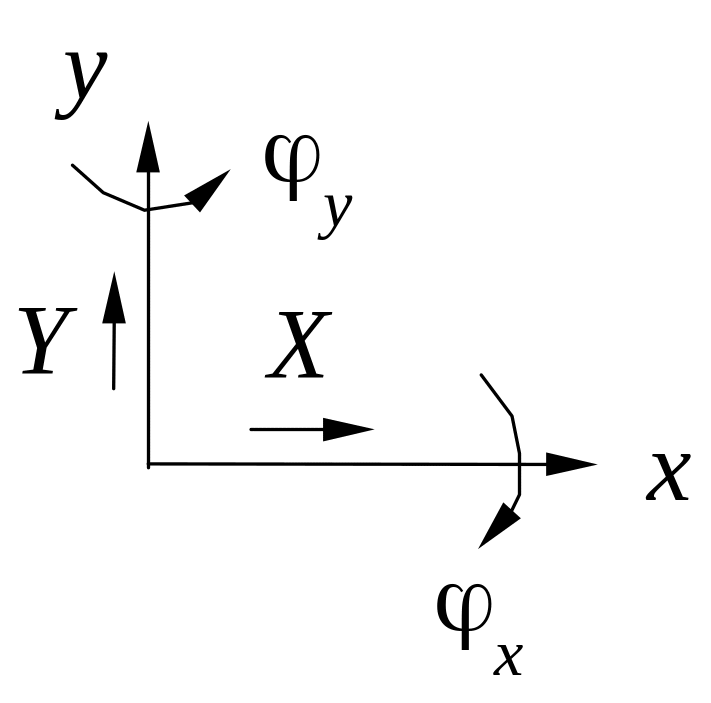5. Кинематические цепи
Звенья, объединенные между собой посредством кинематических пар, образуют кинематическую цепь.
Кинематические цепи подразделяют: на простые (рис. 1.4,а), если все звенья цепи входят не более чем в две кинематические пары; сложные (рис. 1.4,б), если хотя бы одно звено цепи входит больше чем в две кинематические пары; незамкнутые (рис. 1.4,а,б), если в цепи есть звенья, входящие только в одну кинематическую пару; замкнутые (рис. 1.4,в), если все звенья цепи входят в две или более кинематические пары.
Рис. 1.4. Кинематические цепи:
а – простая (незамкнутая); б – сложная незамкнутая;
в – простая замкнутая; 1, 2...6 – звенья;
А, В...L – кинематические пары
Замкнутые неизменяемой конфигурации контуры, представляющие одно звено, на структурных схемах заштриховываются (рис. 1.4,б, звено 3). Звенья, входящие только в одну кинематическую пару, называются поводками.
Элементы кинематических пар звеньев, которыми они присоединяются впоследствии к другим кинематическим цепям или звеньям, называются внешними.
6. Пространства, в которых существуют современные механизмы
Элементарные и простые механизмы могут существовать в различных как по мерности М, так и по подвижности П пространствах и поверхностях, а сложные механизмы могут образовываться из простых, которые функционируют как в одном, так и в разных пространствах и поверхностях (плоскостях).
Для удобства дальнейшего анализа механизмов в табл. 1.3 приведена систематизация пространств.
Т а б л и ц а 1.3
Пространства и механизмы, существующие в них
№ п/п |
Вид пространства |
Мер-ность прост- ран- ства |
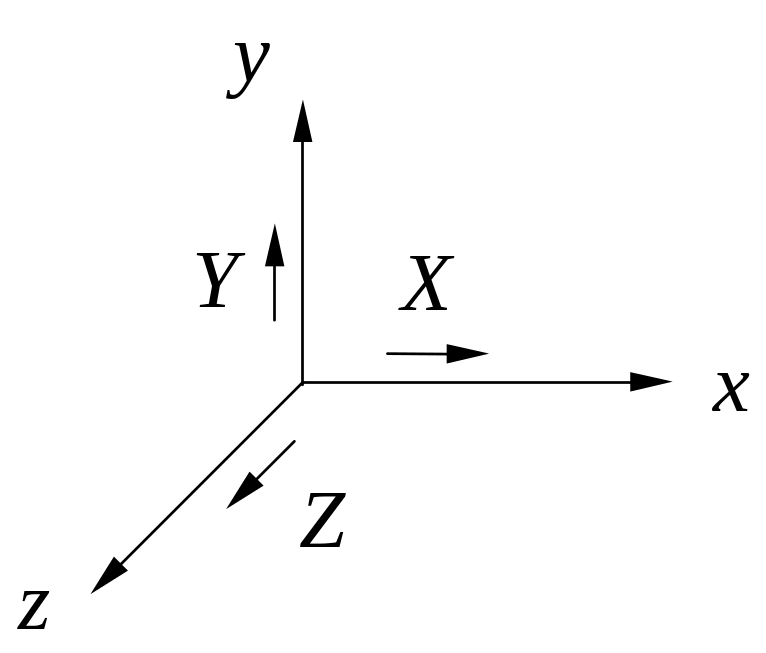
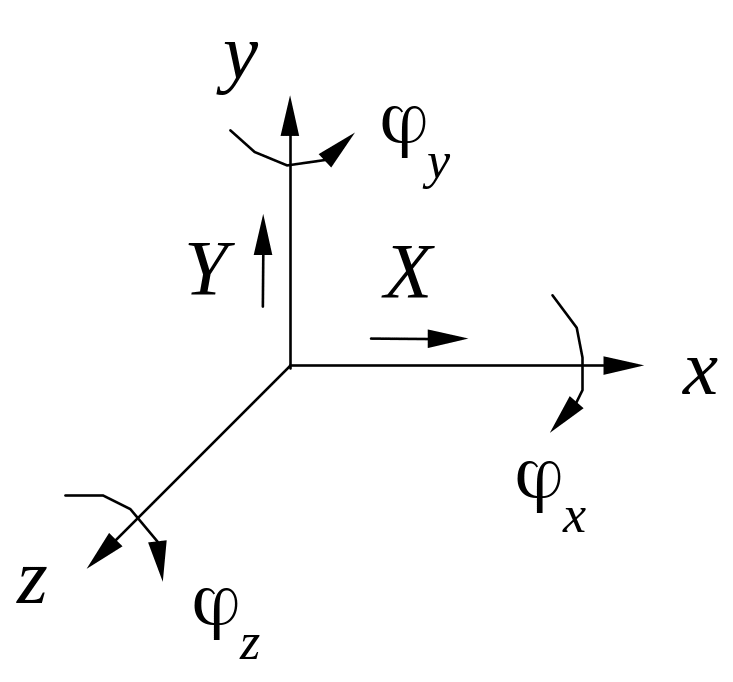
Виды движения |
Подвиж-ность простран- ства |
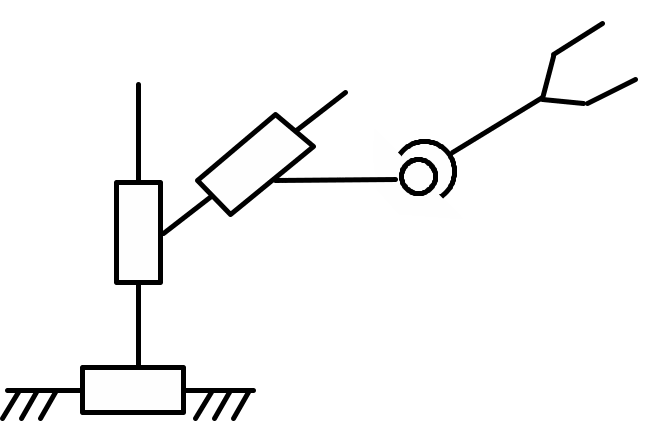
Пример механизма |
Уравне- ния статики |
1 |
|
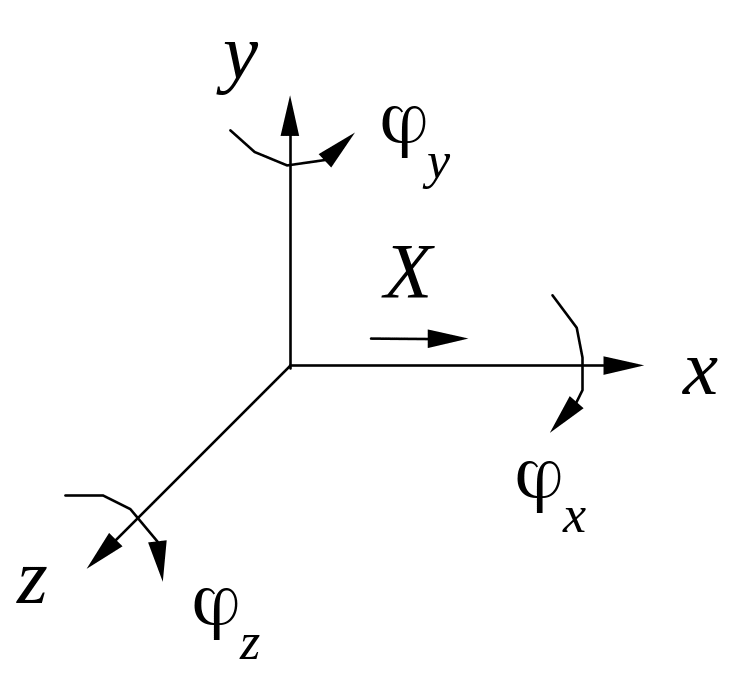
1 |
x |
1 |
|
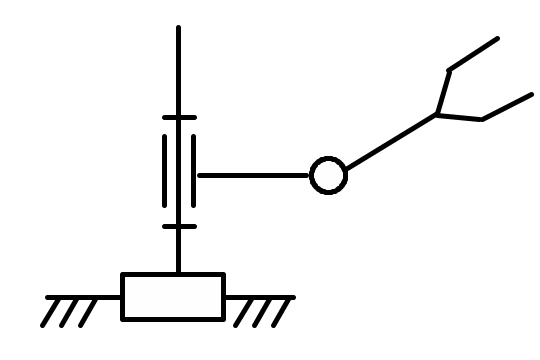
Fрпрx = 0 |
2 |
|
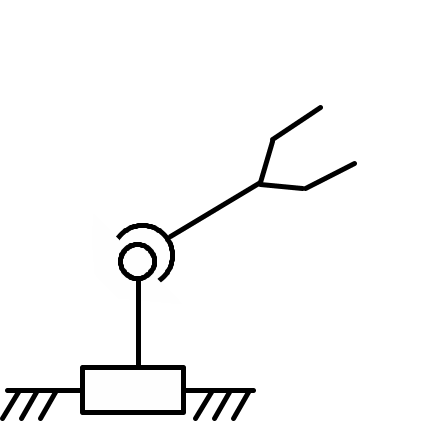
1 |
x |
1 |
|
Mx = 0 |
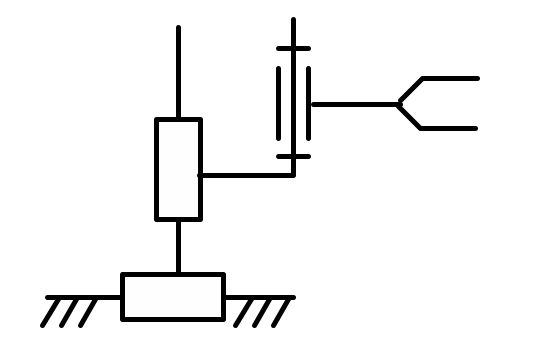
3 |
|
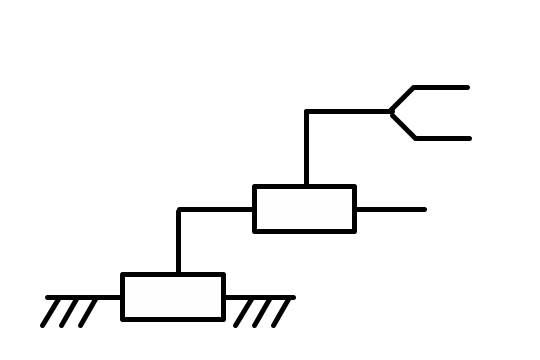
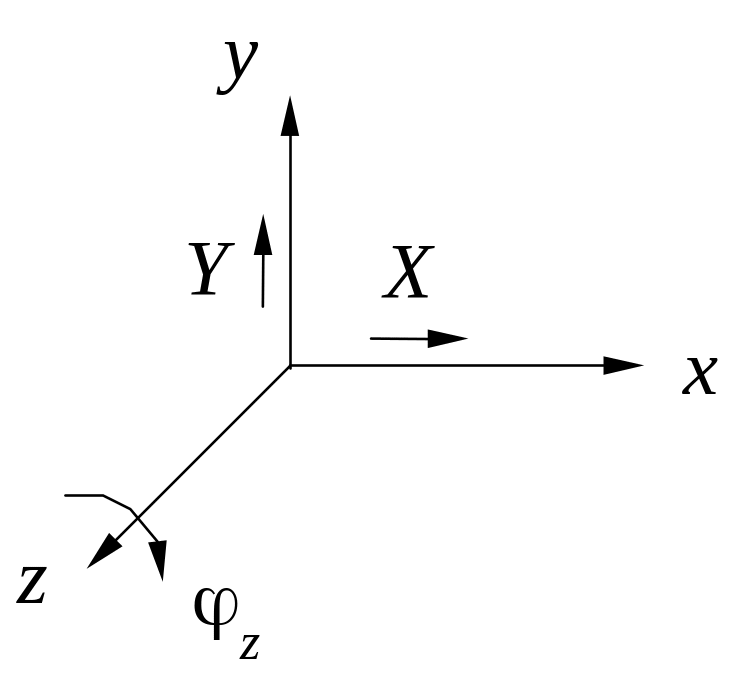
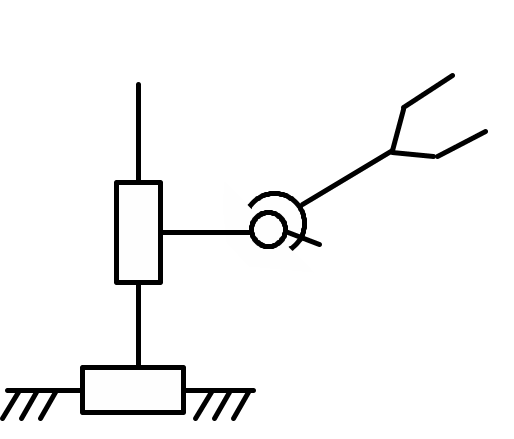
1 |
X, x |
2 |
|
Fx = 0 Mx = 0 |
4 |
|
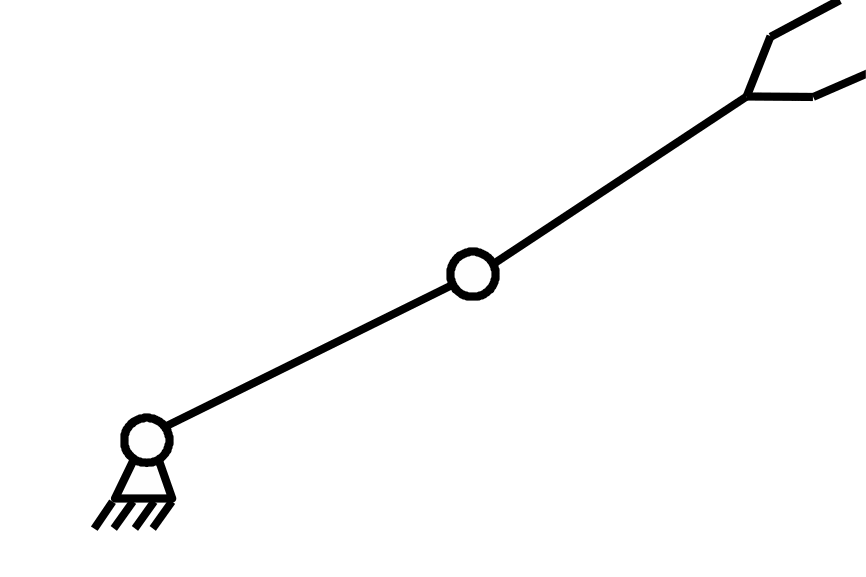
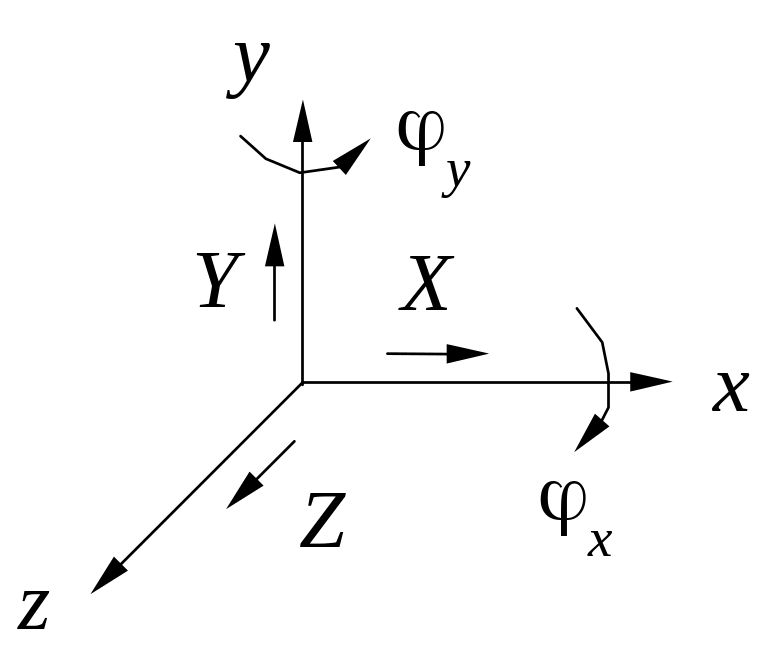
2 |
X, Y |
2 |
|
Fx = 0 Fy = 0
|
П р о д о л ж е н и е т а б л. 1.3
№ п/п |
Вид пространства |
Мер-ность прост- ран- ства |
Виды движения |
Подвиж-ность простран- ства |
Пример механизма |
Уравне- ния статики |
5 |
|
2 |
X, y |
2 |
|
Fx = 0 My = 0 |
6 |
|
2 |
Y, x |
2 |
|
Fy = 0 Mx = 0 |
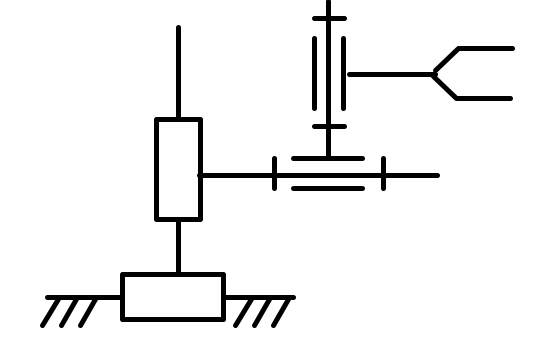
7 |
|
2 |
X, Y, x |
3 |
|
Fx = 0 Mx = 0 Fy = 0 |
8 |
|
2 |
X, Y, y |
3 |
|
Fx = 0 My = 0 Fy = 0 |
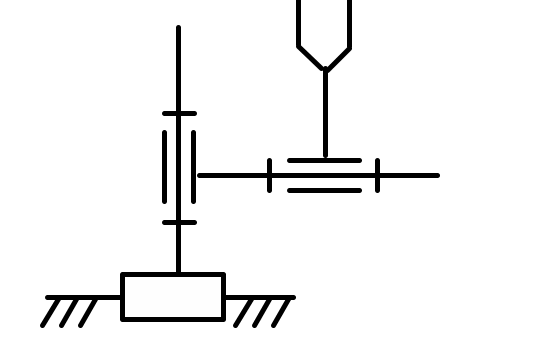
9 |
|
2 |
Y, x, y |
3 |
|
Fy = 0 Mx = 0 My = 0 |
10 |
|
2 |
X, x, y |
3 |
|
Fx = 0 Mx = 0 My = 0 |
П р о д о л ж е н и е т а б л. 1.3
№ п/п |
Вид пространства |
Мер- ность прост- ран- ства |
Виды движе- ния |
Под- виж- ность про- стран- ства |
Пример механизма |
Уравне- ния статики |
11 |
|
3 |
X, Y, Z |
3 |
|
Fx = 0 Fy = 0 Fz = 0 |
12 |
|
3 |
x, y, z |
3 |
|
Mx = 0 My = 0 Mz = 0 |
13 |
|
3 |
X, Y, Z (Z, X, y) (Y, Z, x) |
3 |
|
Fx = 0 Mz = 0 Fy = 0 |
14 |
|
3 |
X, y, z (Y, x, z) (Z, x, y) |
3 |
|
Fx = 0 My = 0 Mz = 0 |
15 |
|
2 |
X, Y, x, y |
4 |
|
Fx = 0 Mx = 0 Fy = 0 My = 0
|
16 |
|
3 |
X, Y, Z, z (X, Y, Z, Х) (X, Y, Z, Y) |
4 |
|
Fx = 0 Mz = 0 Fy = 0 Fy = 0 |
О к о н ч а н и е т а б л. 1.3
№ п/п |
Вид пространства |
Мер- ность прост- ран- ства |
Виды движе- ния |
Под- виж- ность про- стран- ства |
Пример механизма |
Уравне- ния статики |
17 |
|
3 |
X, x, y, z (Y, x, y, z) (Z, x, y, z) |
4 |
|
Fx = 0 Mx = 0 My = 0 Mz= 0 |
18 |
|
3 |
X, Y, x, z (X, Y, y, z) (X, Z, x, y) (X, Z, y, z) (Y, Z, x, y) (Y, Z, x, z) |
4 |
|
Fx = 0 Mx = 0 Fy = 0 Mz= 0
|
19 |
|
3 |
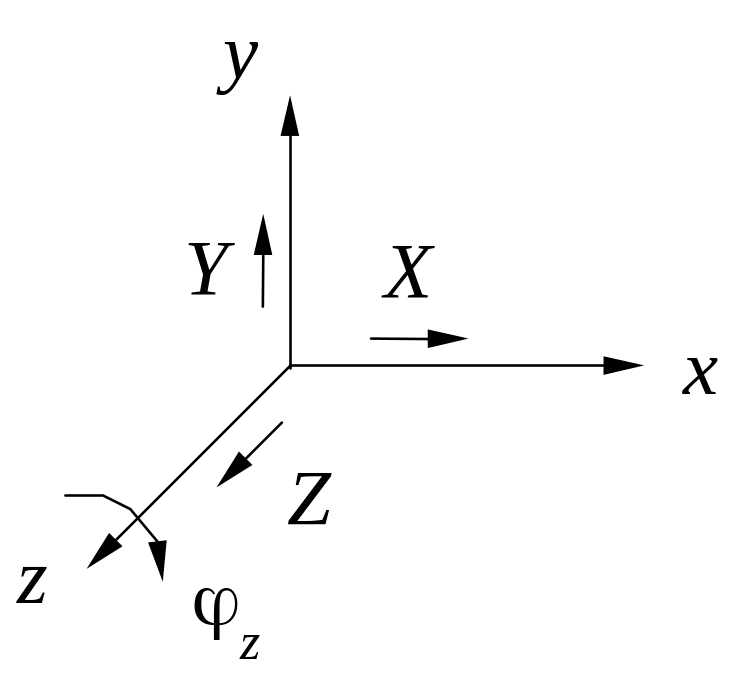
X, Y, Z, x, y (X, Y, Z, x, z) (X, Y, Z, z, y) |
5 |
|
Fx = 0 Mx = 0 Fy = 0 My= 0 Fz = 0 |
20 |
|
3 |
X, Y, x,y,z (X, Z, x,y,z) (Z, Y, x,y,z) |
5 |
|
Fx = 0 Mx = 0 Fy = 0 My= 0 Mz= 0 |
21 |
|
3 |
X, Y, Z, x,y,z |
6 |
|
Fx = 0 Mx = 0 Fy = 0 My= 0 Fz = 0 Mz= 0 |
Примечание. В скобках записаны вырожденные, с точки зрения структуры механизмов, пространства.
Приведенные в табл. 1.3 механизмы существуют в разомкнутом пространстве (плоскости), однако анализ известных в настоящее время механизмов показывает, что среди них есть такие, которые существуют как в открытых пространствах (плоскостях), так и на различных как замкнутых, так и разомкнутых поверх-ностях.
Такими механизмами, например, являются широко известные сферический четырехзвенник (рис. 1.5,а) и шарнир Гука (рис. 1.5,б), цилиндрический клиновой механизм (рис. 1.5,в). Существует большое множество и других механизмов, которые работают, например, на цилиндрах, конусах, эллипсоидах и других поверхностях.
Отметим, что, как и в открытых пространствах, основным параметром, характеризующим структуру механизма, находящегося на поверхности, также будет число степеней свободы или, что одно и то же, число независимых возможных перемещений (подвижность).
Рис. 1.5. Механизмы, существующие на различных поверхностях:
а – сферический четырехзвенник; б – шарнир Гука; в – цилиндрический
клиновой механизм
Сложные механизмы могут получаться в результате объединения между собой простых механизмов, существующих:
в одном по мерности и числу простейших независимых движений пространстве;
в разных по мерности, но одинаковых по числу независимых движений пространствах;
в одном по мерности, но разных по числу независимых движений пространствах;
в пространствах, поверхностях и плоскостях.