Кинематические пары и их классификация

№ п/п	Рисунок	Назва- ние пары	Условное обозначение	Под-вижность пары	Выс- шая Низ- шая	Гео- метри- ческая Сило- вая
1		Враща- тель- ная		1	Н	Г
2		Посту- патель- ная		1	Н	Г
3		Винтовая		1	Н	Г

О к о н ч а н и е т а б л. 1.2

№ п/п	Рисунок	Назва- ние пары	Условное обозначение	Под-вижность пары	Выс- шая Низ- шая	Гео- метри- ческая Сило- вая
4		Цилинд- ричес- кая		2	Н	Г
5		Сфери- ческая		3	Н	Г С
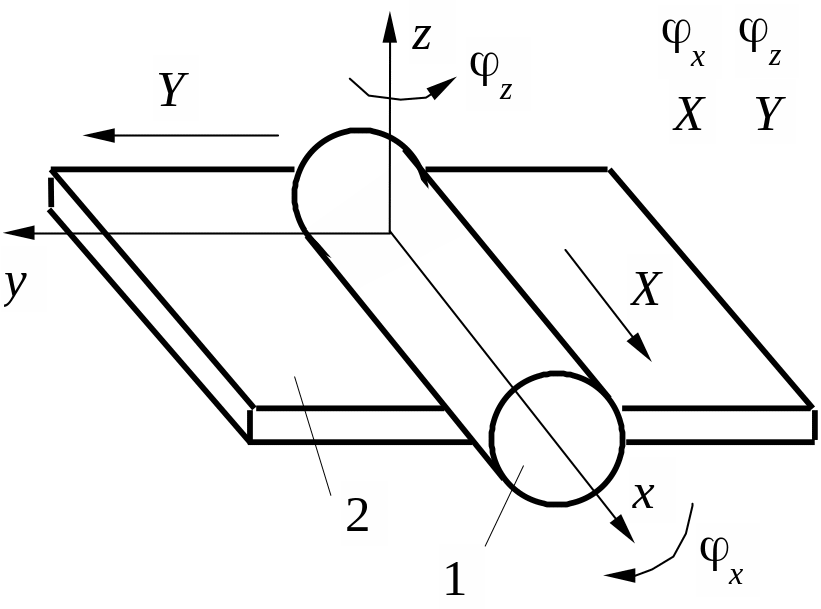
6		Цилиндр – плоскость		4	В	С
7		Шар – плос-кость		5	В	С

Звенья при объединении их в кинематическую пару взаимодействуют между собой по поверхностям, линиям и точкам.

Элементами кинематической пары называют совокупность поверхностей, линий или точек, по которым происходит подвижное соединение двух звеньев.

В зависимости от вида контакта элементов кинематических пар различают высшие и низшие кинематические пары.

Кинематические пары, образованные элементами в виде линии или точки, называются высшими.

Кинематические пары, образованные элементами в виде поверхностей, называются низшими.

Чтобы пара существовала, элементы входящих в нее звеньев должны находиться в постоянном контакте, т.е. быть замкнутыми. Замыкание кинематических пар может быть геометрическим или силовым, например, с помощью собственной массы, пружин и т.п.

Иногда кинематические пары разделяют на закрытые и открытые.

Кинематические пары, полученные в результате силового замыкания образующих их звеньев, считают открытыми, а геометрического – закрытыми.

Кинематические пары разделяют также по числу степеней свободы (подвижности), которые она представляет соединенным посредством ее звеньям, или по числу условий связей (класс пары), налагаемых парой на относительное движение соединяемых звеньев.

Можно подобрать такую форму элементов пары, чтобы при одном независимом простейшем движении возникало второе – зависимое (производное). Такие кинематические пары носят название траекторных.

Т

Рис. 1.3. Сферическая с пальцем

кинематическая пара

раекторные кинематические пары широко применяются в зубчатых, кулачковых, винтовых и других механизмах. Они также часто используются для получения сложных кинематических пар с целью ограничения подвижности простой пары. Так на рис. 1.3 показана сложная кинематическая пара, которая называется сферическая с пальцем.

В получившейся кинематической паре, показанной на рис. 1.3, объединены две – сферическая и траекторная, поэтому ее называют сложной. Из рис. 1.3 видно, что в этой паре, в отличие от сферической (табл. 1.2), возможны только два независимых движения. Третье независимое вращение невозможно из-за наличия в паре пальца. Поэтому сферическая с пальцем кинематическая пара является двухподвижной.

Винтовая пара также является траекторной (табл. 1.2). В этой паре вращательное движение винта (гайки) вызывает поступательное его (ее) перемещение вдоль оси. Такую пару следует отнести к одноподвижной, так как в ней реализуется всего одно независимое движение.