18. Структурная математическая модель механизмов с замкнутыми кинематическими цепями

Для построения структурной математической модели меха-низма введем понятие t-вершинного звена. Число вершин в этом звене определяется числом элементов кинематических пар, которыми оно соединяется с другими звеньями механизма и стойкой.

Если звено имеет в своем составе два элемента кинематических пар (t = 2), то назовем его двухвершинным или линейным звеном; три (t = 3) – трехвершинным звеном; четыре (t = 4) – четырехвершинным и т. д. Графически это выглядит следующим образом:

 одновершинное (линейное) звено (t = 1);

 двухвершинное (линейное) звено (t = 2);

– трехвершинное звено (t = 3);

 четырехвершинное звено (t = 4);

– условное обозначение элемента враща­тельной,

поступательной и высшей кинематической па-

ры соответственно.

Кроме того, введем также понятие числа S элементов кинематических пар, посредством которых кинематические цепи механизма присоединяются к стойкам. На схемах это будет выглядеть следующим образом:

– элемент вращательной кинематической пары;

– элемент поступательной кинематической пары;

С учетом введенных понятий и взяв за базовое звено в синтезируемом (анализируемом) механизме вершинник(и) Т с наибольшим числом элементов кинематических пар, получим соответственно:

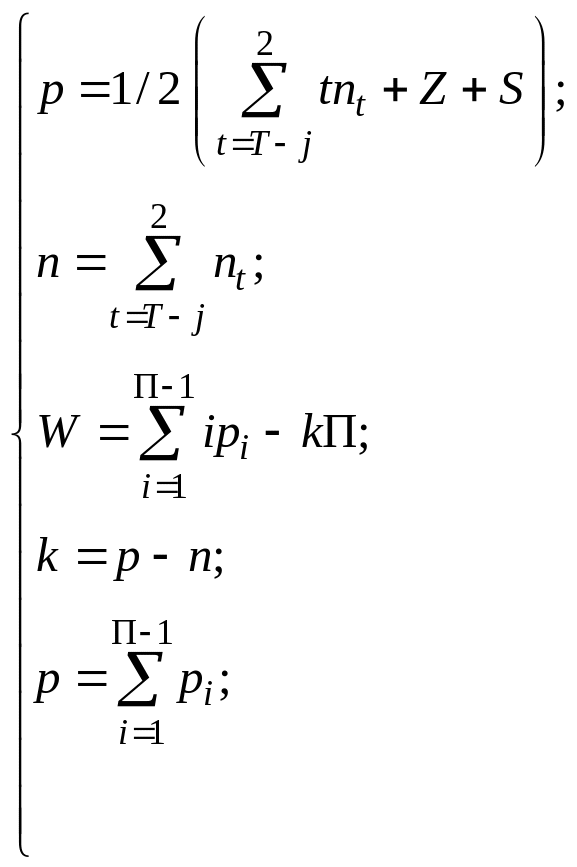(1.18)

(1.19)

где n_t – число подвижных; t – вершинных звеньев; z – число закреплений. Системы уравнений (1.18) и (1.19) – равнозначные структурные математические модели простых и сложных однотипных механизмов с замкнутыми кинематическими цепями.

19. Структурный анализ механизмов с использованием структурной математической модели

Покажем на примерах эффективность применения структурных математических моделей при анализе механизмов.

Пример 1. Проверить, является ли прямило (инверсор) Поселье–Липкина (рис. 1.19,а) механизмом.

Рис. 1.19. Инверсор Поселье-Липкина:

а – схема со сложными шарнирами; б – развернутая схема

Анализ возможных независимых простейших движений показывает, что этот механизм существует в трехподвижном пространстве (П = 3), допускающем перемещения вдоль осей X и Y и вращение вокруг оси Z. Инверсор с учетом того, что в нем установлены сложные кинематические пары, имеет десять одно-подвижных кинематических пар и семь звеньев. Предварительный анализ показывает, что инверсор состоит из линейных звеньев, для которых Т = 2, и имеет два присоединения к стойке.

Подставим полученные исходные данные в уравнения структурной математической модели, например (1.18), в результате получим:

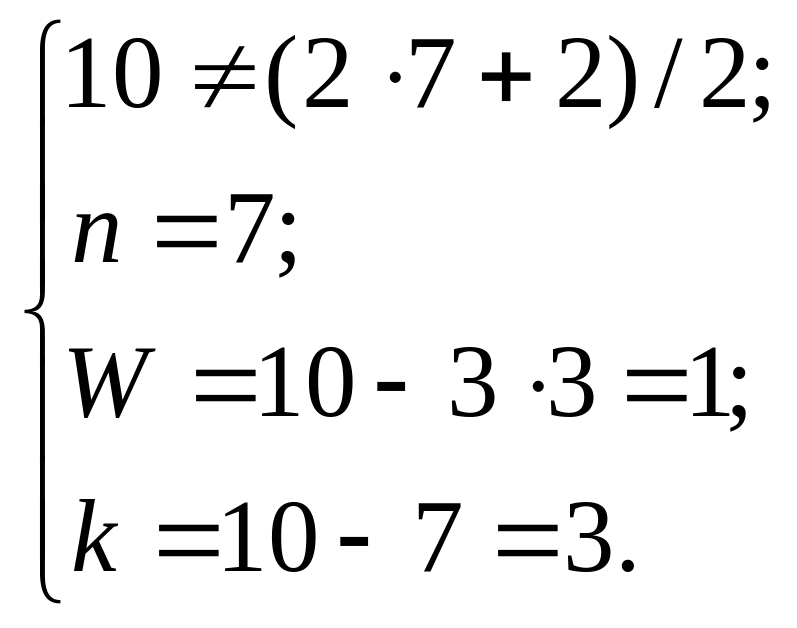(1.20)

Так как первое уравнение в (1.20) не превратилось в тождест-во, то это означает, что либо исследуемое устройство не механизм, либо при анализе неверно были определены исходные данные.

Как показывает повторный анализ инверсора, ошибка была допущена из-за того, что кинематические пары В, В, С, С, Е, Е и F, F являются сложным шарниром и изображены на схеме совмещенными, поэтому на предыдущем этапе неверно были определены вид звеньев и число присоединений к стойке. Действительно, если нарисовать развернутую схему исследуемого механизма (рис. 1.19,б), то станет видно, что его базовое звено имеет три элемента кинематических пар (Т = 3), а сам механизм – три присоединения к стойке (S = 3). С учетом сказанного последнее выражение (1.20) запишется следующим образом:

10 = (3 × 3 + 2 × 4 + 3)/2 = 10,

т. е. оно превратилось в тождество, а значит, инверсор Поселье–Липкина является одноподвижным механизмом.