Порядок выполнения работы

Упражнение 1. Измерение давления при разных временах запаздывания.

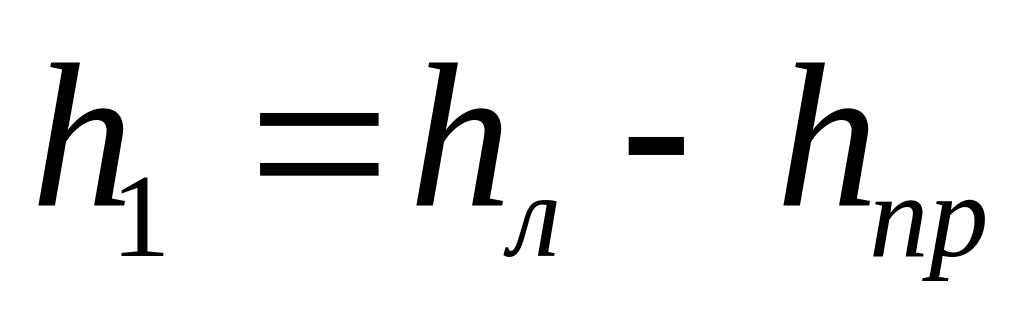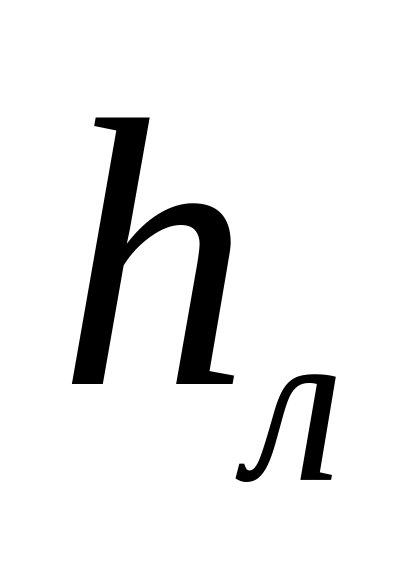1. С помощью насоса накачать в баллон воздух, доведя показания уровня воды в левой трубке манометра до 20 делений (20 см), подождать 2-3 мин, пока температура в баллоне не уравняется с комнатной. Определить давление газа в баллоне по формуле , где и 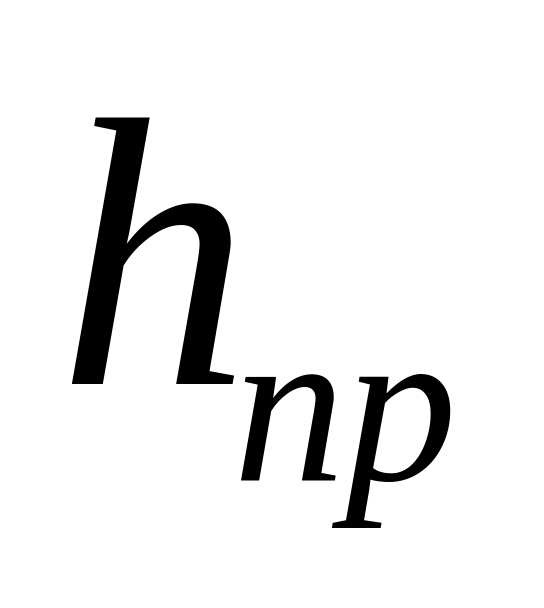- высота уровня воды в левой и правой трубках манометра соответственно.

2. Быстро открыть кран 3, одновременно включить секундомер. Через 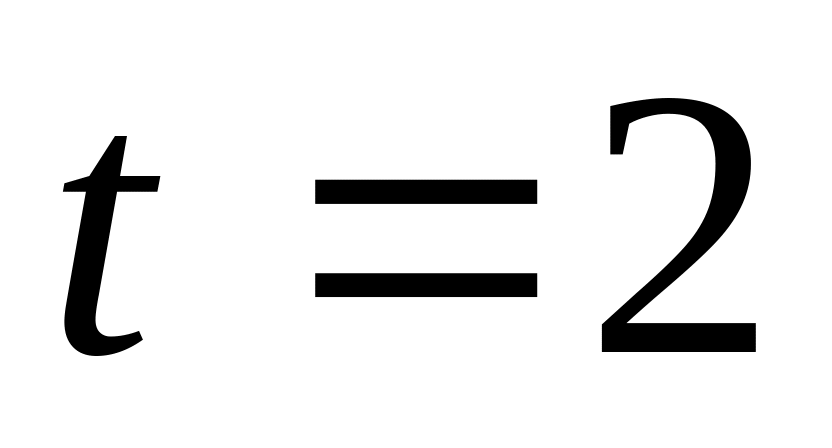с кран 3 перекрыть.

3. После перекрытия крана давления в баллоне начинает расти. Через 2-3 мин определить давление газа в баллоне по формуле .

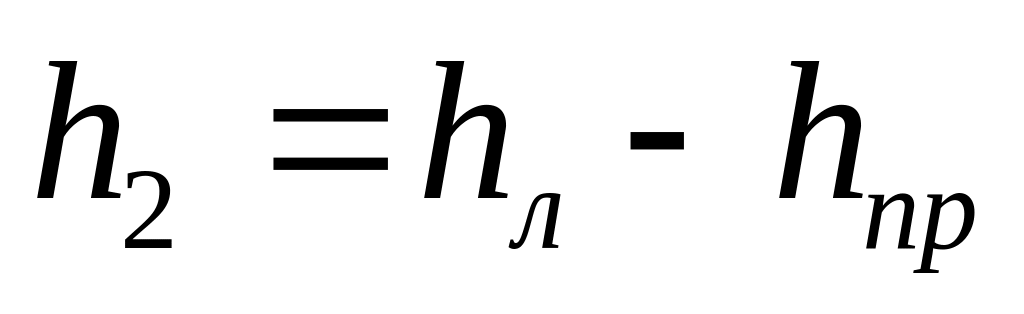4. Повторить измерения при 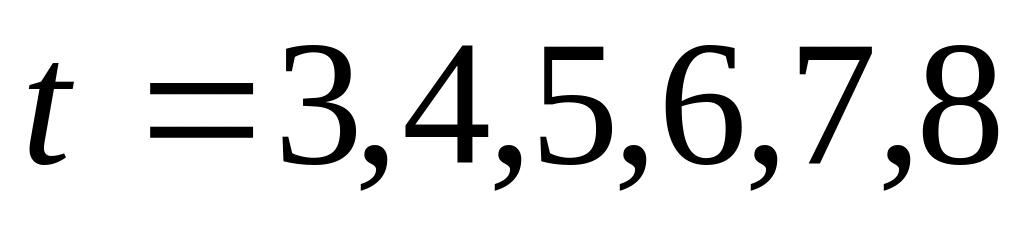с. Следить за тем, чтобы начальное давление в каждом опыте было одним и тем же. то есть . Результаты измерений занести в таблицу по форме 22.1, рассчитав

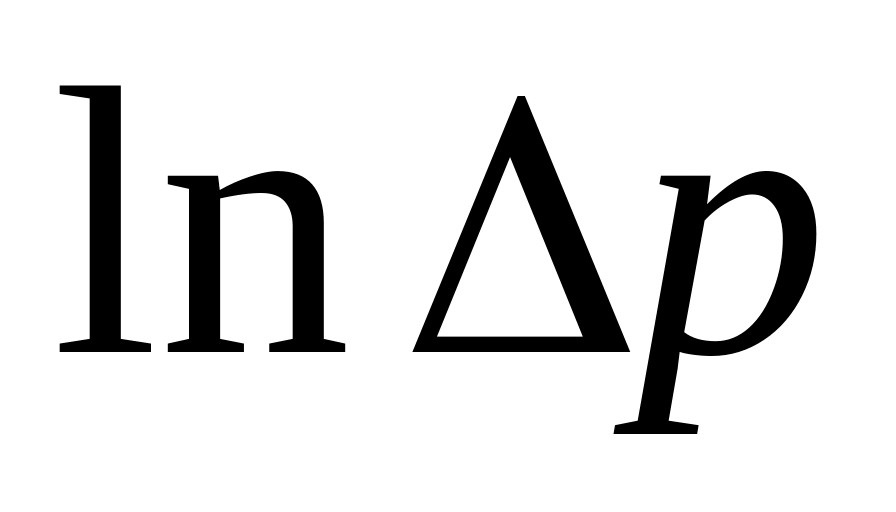
Упражнение 2: Определение истинного значения p графическим путем и вычисление величины показателя адиабаты

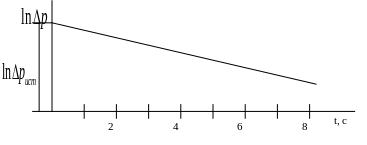
Рис. 22.3

1. По данным измерений построить график lnp=f(t) (рис.22.3). По графику определить p_ист, т.е. 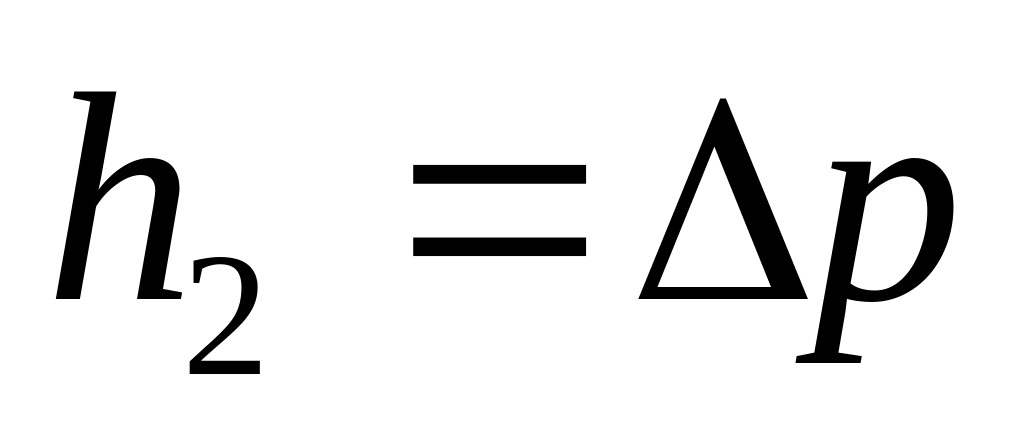, соответствующее мгновенному адиабатическому расширению газа (формула 22.12).

2. По формуле (22.5) вычислить величину . Вычислить абсолютную и относительную погрешность ,

3. Записать все результаты вычислений в таблицу по форме 22.2

Форма 22.1.

t , с	2	3	4	5	6	7	8
p, дел
ln p

Форма 22.2

, дел	, дел

Контрольные вопросы

1. Запишите первое начало термодинамики для изохорного, изотермического и адиабатического процессов.

2. Почему теплоемкость газа зависит от способов и условий нагревания?

3. Какая физическая величина в первом начале термодинамике не зависит от характера процесса?

4. Почему С_p больше C_v ?

5. Какой процесс называется адиабатическим? Как связаны параметры состояния идеального газа при адиабатическом процессе?

6. Объясните каким образом и почему меняется температура газа в баллоне.

7. Нарисуйте на p-V диаграмме все процессы, происходящие с газом в этом опыте.

8. Получите рабочую формулу (22.15) для определения

9. Объясните, почему необходимо измерять зависимость ? При изменении состояния газа от 1 к 2?

Используемая литература

[2]§83, 88; [3]§9.1-9.6; [7]§55; [4]§34; [5]§34.1-34.4.

Лабораторная работа 1-23 “Определение отношения акустическим методом”

Цель работы: изучить рспространение звуковых волн в газах, определить адиабатическую постоянную воздуха.

Теоретическое введение.

Термодинамические соотношения, определяющие величины теплоёмкостей при постоянном давлении ( ) и при постоянном объёме ( ) приведены в работе 1-22 “Определение отношения газовых постоянных адиабатическим методом”. Там же отмечено, что отношение определяет скорость распространения звука в газах. Поэтому, измеряя величину скорости звука в газе, можно определить значение адиабатической постоянной .

Рассмотрим, чем определяется скорость звуковых волн в газе и как она зависит от температуры. Звуковыми или акустическими волнами называют упругие волны малой интенсивности, т.е. слабые механические возмущения (деформации), распространяющиеся в упругой среде. В сплошной среде любую малую деформацию можно представить в виде элементарных деформаций растяжения (сжатия) и сдвига. Поэтому упругие свойства изотропных твердых тел вполне определяются двумя упругими константами – модулем Юнга (растяжение, сжатие) и модулем сдвига (чистый сдвиг). И соответственно в твердых телах могут распространяться продольные волны (волны сжатия, растяжения) и поперечные волны (волны сдвига).

Что же касается газов, то они в отличие от твердых тел способны как угодно изменить свою форму под действием сколь угодно малых сил. Лишь для изменения самого объема газа как и для твердых тел, необходимы конечные внешние силы. Т.е. газы ведут себя как упругие тела только в отношении изменения объема. Из двух элементарных деформаций – растяжения (сжатия) и сдвига – только первая связана с изменением объема. Поэтому только в отношении деформации растяжения и сжатия газы ведут себя как упругие тела. Однако и в отношении этой деформации есть существенное различие в поведении газов от твердых тел. Твердое тело можно растянуть или сжать в каком–либо одном направлении. Его можно также сжать во всех направлениях, т.е. подвергнуть всестороннему сжатию или растяжению. В газах же имеем дело только со всесторонним сжатием (только деформации сжатия). Какой бы объем ни занимала данная масса газа, газ всегда оказывается сжатым, так как в отсутствие внешних сил объем газа будет увеличиваться беспредельно. Итак, газы ведут себя как упругие тела только в отношении деформации всестороннего сжатия.

Давление в газе зависит от степени его сжатия. Так же, как и в твердых телах, связь между давлением (напряжением) и сжатием (деформацией) определяется упругими свойствами тела. Упругие свойства газа характеризуются объемной упругостью (сжимаемостью), то есть соотношением между изменением объема (плотности) данной массы газа и изменениями давления в нем. Объемная упругость жидкостей и газов количественно может быть охарактеризована отношением действующего давления к величине относительного изменения объема, которое этим давлением вызвано.

Пусть объём газа при некотором нормальном давлении равен и при изменении давления на он изменится на . Следовательно, относительное изменение объёма есть , а коэффициент сжимаемости определяют как:

(23.1)

Обратная величина называется модулем сжатия:

(23.2)

Знак минус взят затем, чтобы было положительно ( и всегда противоположны по знаку).

Если выразить (23.2) через плотность ( ), то получим:

(23.3)

Найдем теперь, как связана скорость звуковых волн в газе с его упругими свойствами – с модулем сжатия. Звуковая волна в газе представляет собой последовательные чередующиеся области сжатия и разрежения, распространяющиеся со скоростью, зависящей от упругих свойств газа.

Как может возникнуть область сжатия в газе?

Представим себе пластину очень больших размеров, помещённую в газ (рис.23.1). Сообщив пластине быстрое перемещение со скоростью вдоль нормали к ней, мы вызовем в прилегающем слое газа сжатие и вследствие этого повышение давления. Это давление вызовет движение следующего слоя газа и т.д. Сжатие будет передаваться от слоя к слою; в газе будет распространяться импульс сжатия. Рассчитываем скорость его распространения.

П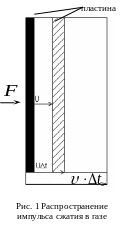 усть импульс сжатия соответствует увеличению плотности на и увеличению давления на . Через площадку за время проходит часть импульса сжатия , где - скорость распространения импульса. Прохождение этого участка импульса сжатия связано с увеличением массы справа от площадки на величину ( , ; - плотность газа в области сжатия; - плотность недеформированного газа). При этом через площадку передается количество движения . Вместе с тем слева на площадку действует сила . Изменение количества движения должно быть равно по второму закону Ньютона. Следовательно:

, или

(23.4)

Таким образом, скорость распространения области сжатия в газе определяется тем, как изменяется его плотность при изменении давления.

Чтобы получить теперь окончательное выражение для скорости звука в газе, необходимо принять во внимание, что упругие свойства газов зависят от температуры. При быстром сжатии газа выделяется тепло, которое не успевает распространиться в соседние объёмы. Сжатие газа без отвода тепла – это адиабатический процесс. При адиабатическом изменении состояния газа вместо закона Бойля-Мариотта, который справедлив при неизменной температуре (изотермическое сжатие), связь между объёмом и давлением дается уравнением Пуассона

, (23.5)

где .

Так как плотности обратно пропорциональны объемам, то уравнение Пуассона можно переписать так

Или

(23.6 )

Дифференцируя (23.6), находим

(23.7)

Если сравнить выражение ( - модуль Юнга), определяющее скорость распространения продольных звуковых волн в твердых телах, (23.3), (23.4) и (23.7) то видно, что величина играет в газе такую же роль, какую величина в твердом теле. Эта величина и определяет скорость распространения области сжатия. В отличие от модуля Юнга твердого тела, модуль сжатия газа зависит от того значения плотности , которое имеет газ в области сжатия.

Только в том случае, когда сжатие столь мало, что можно положить , модуль сжатия перестает зависеть от и скорость распространения области сжатия не зависит от величины сжатия (деформации).

В этом случае, как следует из (23.7)

(23.8)

и скорость распространения слабых импульсов сжатия:

(23.9)

Звуковые волны можно рассматривать как ряд таких импульсов сжатия, следующих вплотную друг за другом и распространяющихся с одинаковой скоростью. Пока сжатия в звуковой волне не велики, она должна распространяться со скоростью, определяемой (23.9).

Используем уравнение состояния для идеального газа ( - молярная масса, - универсальная газовая постоянная, - температура) в виде .

Тогда выражение для скорости звуковых волн в идеальном газе принимает такой вид:

(23.10)

Отсюда отношение газовых теплоемкостей:

(23.11)

Из него следует, что для определения адиабатической постоянной достаточно при постоянной температуре в газе измерить скорость звука.

Отметим еще, что формула (23.10) имеет ясный физический смысл: передача возмущений в звуковой волне в газе осуществляется за счет теплового движения молекул, поэтому не удивительно, что скорость звука равна по порядку величины скорости теплового движения молекул