По второму закону Ньютона для вращательного движения маятника:

, (19.7)

где – момент инерции маятника относительно оси, проходящей через точку подвеса;  – угловое ускорение маятника, равное второй производной угла поворота: .

Из уравнений (19.6) и (19.7) имеем:

,

или

. (19.8)

При малых углах , и уравнение (19.8) будет иметь вид:

. (19.9)

Сравнивая (19.9) и (19.5), устанавливаем, что  изменяется по гармоническому закону с круговой частотой ω, причем

, (19.10)

а период колебаний маятника

. (19.11)

Если вся масса маятника сосредоточена в одной точке (например, шарик, подвешенный на невесомой нерастяжимой нити), то такой маятник называют математическим (рис.19.3). В других случаях маятник называют физическим.

П

Рис.19.3

риведенной длиной физического маятника называется длина такого математического маятника, который имеет тот же период колебаний, что и данный физический маятник:

. (19.12)

Для математического маятника момент инерции рассчитывается как для материальной точки: , поэтому период его колебаний равен:

. (19.13)

В лабораторной работе используется физический маятник в виде кольца (рис.19.4) или в виде однородного тонкого стержня (рис.19.5). Момент инерции маятника относительно точки подвеса О можно найти по теореме Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс параллельно данной оси, и произведения массы тела на квадрат расстояния между осями. Для кольца получим:

. (19.14)

З

Рис.19.4

десь – момент инерции маятника относительно оси, проходящей через точку подвеса O, I_C – момент инерции относительно оси, проходящей через центр масс – точку C, r – расстояние между осями. Момент инерции полого (толстостенного) цилиндра или кольца массой m с внутренним радиусом r и наружным R относительно оси, проходящей через центр масс, равен:

I_C= m(R²+r²), (19.15)

Тогда из (19.14) и (19.15) получаем:

I_O= m(R²+r²)+mr²= m(R²+3r²) = m(D²+3d²), (19.16)

где и – внешний и внутренний диаметры диска соответственно. Из формулы (19.11) выразим ускорение свободного падения с учетом, что l=r=d/2, и из (19.16) подставим момент инерции:

,

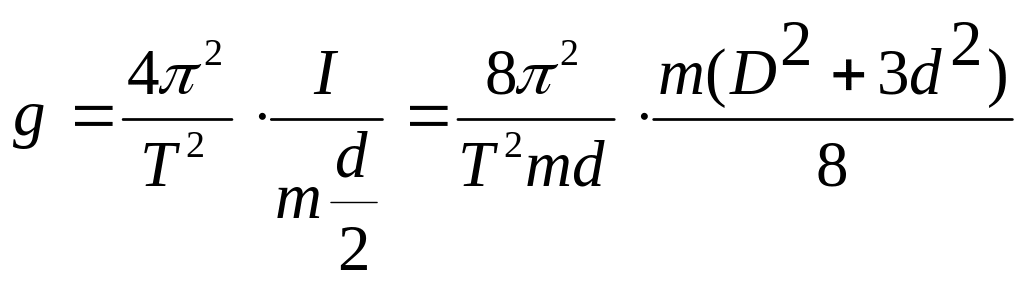и окончательно:

. (19.17)

Для стержня по теореме Штейнера получим:

, (19.18)

г

L

O

C

O₁

l_пр. l

де I – момент инерции стержня относительно точки подвеса (не совпадающей с центром масс!), l – расстояние между центром масс (центром стержня) и точкой подвеса (длина физического маятника), I_C – момент инерции стержня относительно центра масс:

, (19.19)

где L – длина стержня, m – его масса.

М

Рис.19.5

ожно показать, что для любого маятника приведенная длина l_пр. больше, чем расстояние l от центра масс до точки подвеса (длины физического маятника): из (19.12) и (19.18) следует, что

.

Точка О₁, лежащая на прямой ОС на расстоянии l_пр.от точки подвеса маятника (рис.19.5), называется центром качания маятника. Центр качания О₁ и точка подвеса О обладают свойством взаимности: если маятник подвесить так, чтобы его ось качания проходила через точку О₁, то точка О будет совпадать с новым положением центра качания маятника, то есть приведенная длина и период колебаний маятника останутся прежними. Покажем это. По теореме Штейнера момент инерции I₁ маятника относительно оси, проходящей через точку О₁, равен:

. (19.20)

Из (19.18) и (19.20) вычислим I_C:

I_C= I₁ – ml₁²=I – ml². (19.21)

Из (19.12) выразим момент инерции маятника и запишем аналогичную формулу для I₁: . Здесь использовано условие, что частота колебаний маятника относительно оси, проходящей через точку О₁, должна быть той же самой, что и для оси, проходящей через точку О. Подставив оба момента инерции в (19.21) получим уравнение:

.

Далее после преобразований:

,

и после сокращения на (l₁–l):

.

Но по определению приведенной длины физического маятника (19.12):

,

то есть

l_пр. =l₁+l,

что и требовалось показать.

Для физического маятника – стержня из (19.12), (19.18) и (19.19) получим:

,

или:

. (19.22)