Контрольные вопросы

1. Что такое коэффициент упругости, модуль Юнга?

2. Что такое абсолютное и относительное удлинение образца?

3. Что такое механическое напряжение?

4. Что такое коэффициент Пуассона?

5. Что такое абсолютное и относительное поперечное сжатие?

6. Какие из перечисленных характеристик относятся к материалу?

7. Какие из перечисленных характеристик относятся к образцу?

8. Закон Гука и его физический смысл.

9. Кривая зависимости и ее характерные точки и участки.

10. Деформация сдвига, иллюстрация пластических деформаций.

11. В чем состоит суть данного метода измерения ?

12. Размерность и

13. Порядок величин для различных твердых тел

14. Учитывается ли в опыте масса самого стержня?

15. Почему мы не определяем величины и для сталей?

Используемая литература

[1] §14; [7] §21; [4] §48.

Лабораторная работа 1-18 “Изучение свободных колебаний пружинного маятника”

Цель работы: Определение жесткости пружины, определение периода свободных затухающих колебаний, логарифмического декремента затухания, коэффициента затухания.

Теоретическое введение

Колебаниями называются процессы (движения или изменения состояния), в той или иной степени повторяющиеся во времени. В зависимости от физической природы колебательного процесса различают механические колебания (колебания маятников, струн, частей машин и механизмов, давления воздуха), электромагнитные (переменный ток в цепи, колебания напряженностей электрического и магнитного полей) и др. Однако математическое описание колебаний различной физической природы практически одинаково.

Механическим колебательным движением называется процесс, при котором система (материальная точка, тело, система тел), многократно отклоняясь от положения равновесия, вновь возвращается к нему. Колебания называются периодическими, если система приходит в положение равновесия через равные промежутки времени. Время одного полного колебания называется периодом.

Свободными (собственными) колебаниями называются колебания, которые происходят в отсутствие переменных внешних воздействий на колебательную систему и возникают вследствие начального отклонения этой системы от состояния равновесия.

Гармоническими называются колебания, при которых колеблющаяся величина х изменяется со временем по закону синуса или косинуса:

, (18.1)

здесь – амплитуда колебаний (максимальное значение колеблющейся величины х), – фаза колебаний, – начальная фаза, ω₀ – круговая (циклическая) частота собственных колебаний, связанная с периодом колебаний Т соотношением:

, (18.2)

ν – частота собственных колебаний (число полных колебаний в единицу времени, ).

Для механических колебаний х имеет смысл смещения тела (материальной точки) из положения равновесия. Найдем скорость v и ускорение a колеблющегося тела:

; (18.3)

. (18.4)

Из (18.4) получаем дифференциальное уравнение гармонических колебаний:

. (18.5)

Из (18.5) следует, что если вторая производная по времени какой-либо физической величины (например, смещения) пропорциональна самой величине с противоположным знаком, то данная физическая величина изменяется со временем по гармоническому закону.

К олебательная система будет совершать свободные колебания, если её вывести из положения равновесия и предоставить самой себе. Со свойствами свободных колебаний можно ознакомиться на примере пружинного маятника. Его основными частями являются груз массой m и пружина с коэффициентом жёсткости k (рис.18.1).

Рис.18.1

Рис. 1

Маятник совершает колебания около положения равновесия, двигаясь возвратно-поступательно.

В положении равновесия сила тяжести уравновешивается упругой силой:

(18.6)

где – удлинение пружины под действием груза.

Смещение груза из положения равновесия будет характеризоваться координатой x, причем ось x направлена по вертикали вниз, а нуль оси совместим с положением равновесия. При смещении груза из положения равновесия на расстояние, равное x, удлинение пружины станет равным (l₀+x), тогда полная сила, вызывающая колебания маятника и возвращающая его к положению равновесия, примет значение

. (18.7)

Учитывая условие равновесия (18.6), получим

. (18.8)

При малых деформациях эта сила описывает закон Гука. Выведем уравнение движения маятника на основе второго закона Ньютона: 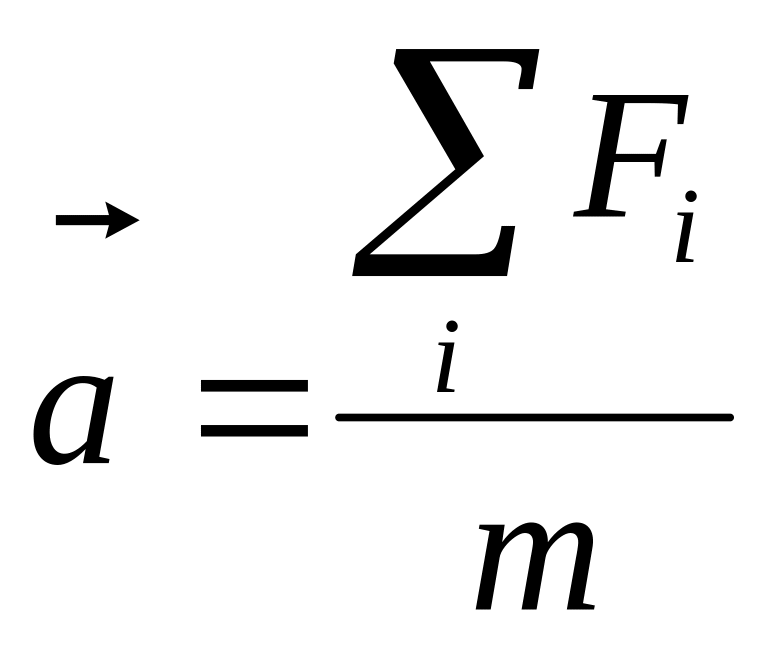. В проекциях на ось х получим:

, (18.9)

или

, (18.10)

где – ускорение, .

Выражение (18.10) совпадает с (18.5), это – дифференциальное уравнение гармонических незатухающих колебаний, а его решение имеет вид:

, (18.11)

где A₀ – амплитуда колебаний, φ₀ - начальная фаза, ω₀ – круговая частота:

. (18.12)

Так как , то период колебаний

. (18.13)

Опыт показывает, что свободные колебания пружинного маятника затухают – амплитуда колебаний груза со временем уменьшается. Причиной затухания колебаний в пружинном маятнике является сила сопротивления среды и связанная с этой силой диссипация энергии – превращение механической энергии колебаний во внутреннюю. Силу сопротивления среды при малых скоростях можно считать пропорциональной скорости движения, а направление её противоположно скорости:

, (18.14)

здесь r – коэффициент сопротивления среды, – скорость движения груза.

В таком случае на маятник действуют две силы – упругая сила (18.8) и сила сопротивления (18.14). По второму закону Ньютона: ; с учетом того, что , получим дифференциальное уравнение свободных затухающих колебаний:

, (18.15)

или

. (18.15’)

Здесь приняты следующие обозначения:

, (18.16)

, (18.17)

где β – коэффициент затухания, – циклическая частота собственных колебаний, то есть колебаний системы, если бы затухания не было.

Решением дифференциального уравнения (18.15) при условии малости затухания (то есть если β < ω₀) является функция

, (18.18)

в чем можно убедиться путем подстановки (18.18) в (18.15), предварительно найдя производные. При этом будет получено и выражение для круговой частоты затухающих колебаний:

. (18.19)

График функции (18.18) приведен на рис.18.2.

Если затухание велико (β > ω₀), движение системы не имеет колебательного характера и будет апериодическим (рис.18.3). Этот случай в дальнейшем рассматриваться не будет.

x(t)

Рис.18.2

A(t)=A₀e^-βt

x(t)

Рис.18.3

Период затухающих колебаний найдем из (18.19):

. (18.20)

Таким образом, если на тело, кроме силы упругости, действует сила сопротивления среды, то тело будет совершать колебательное (но не гармоническое) движение с частотой, зависящей от массы тела m, жесткости пружины k и коэффициента затухания β, характеризующего силу сопротивления среды. При этом частота ω затухающих колебаний оказывается меньше частоты собственных незатухающих колебаний из-за действия тормозящей силы сопротивления. Амплитуда колебаний будет с течением времени уменьшаться по экспоненциальному закону:

, (18.21)

здесь – начальная амплитуда колебаний.

Отношение значений амплитуд затухающих колебаний в моменты времени t и (t+T) называется декрементом затухания:

,

а логарифм декремента затухания называется логарифмическим декрементом затухания:

, (18.22)

Или иначе: логарифмический декремент затухания – это натуральный логарифм отношения амплитуд двух следующих друг за другом колебаний:

, (18.23)

где колебания с номерами n и (n+1) отстоят друг от друга по времени на один период. Если два колебания отстоят друг от друга по времени на N периодов (t=NT), то отношение их амплитуд:

,

откуда следует, что коэффициент затухания

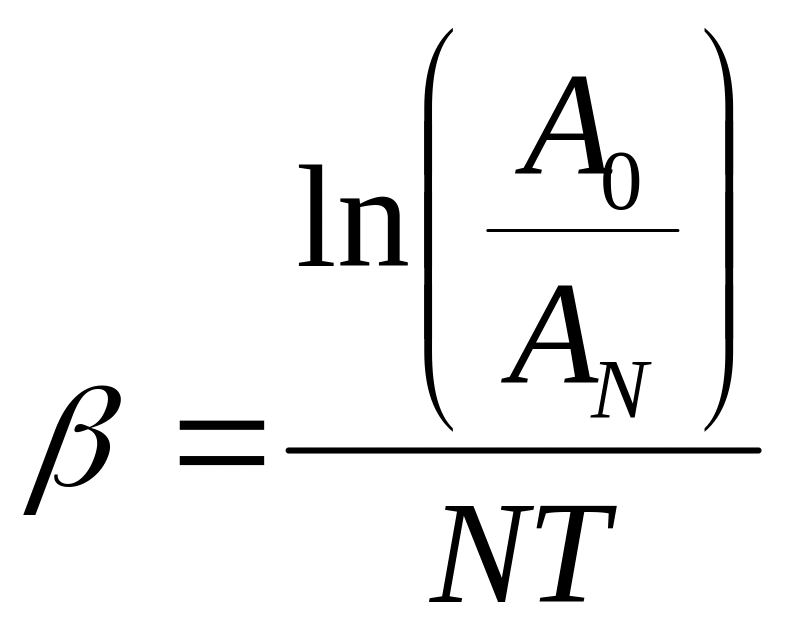, (18.24)

здесь предположили для удобства, что .

Промежуток времени , в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации. Из (18.21) можно получить, что

.

Еще одна важная физическая величина характеризует затухание колебаний – добротность:

. (18.25)

Можно показать, что добротность обратно пропорциональна относительной убыли энергии колебаний за время, равное одному периоду:

. (18.26)