Контрольные вопросы

1. Что такое момент инерции твердого тела?

2. Сформулируйте основной закон динамики вращательного движения.

3. Сделайте подробный вывод формулы (9.19).

4. О каком законе сохранения идет речь в этой работе? Сформулируйте его.

5. Чему равна работа при вращении тела вокруг оси?

6. Дайте представление о моделях тел в механике и приведите примеры.

7. Представьте определение замкнутой системы тел.

8. Чем отличаются консервативные силы от неконсервативных? Приведите примеры.

Используемые литература

[1] §24, 38, 39, 41; [2] §24, 31-33; [3] §3.4; 4.1-4.3; [7] §16, 18; [6] §2.8; 7.1; 7.2.

Лабораторная работа 1-10 “Маятник Максвелла”

Цель работы: применение основных законов динамики к изучению движения твёрдых тел, определение момента инерции маятника Максвелла.

Теоретическое введение

При применении основных законов динамики к изучению движения твердых тел необходимо исходить их того, что в общем случае движение твердого тела определяется двумя векторными уравнениями. Одно из них – уравнение движения центра тяжести твердого тела

, (10.1)

где – масса всего тела; – скорость его центра тяжести; – сумма всех внешних сил, действующих на тело.

Другое – уравнение моментов в системе отсчета, жестко связанной с центром тяжести (в ней покоится центр тяжести)

, (10.2)

где – момент импульса тела относительно оси, проходящей через центр тяжести, а – суммарный момент всех внешних сил относительно этой оси.

П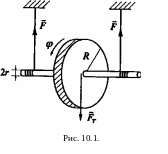 ростейшее движение твердого тела – плоское движение. В этом случае каждая его точка движется, оставаясь в одной из параллельных друг другу плоскостей. Примером плоского движения является качение цилиндра по плоскости. Другим примером является маятник Максвелла, который представляет собой однородный круглый диск радиуса R, подвешенный на двух нерастяжимых нитях, намотанных на его горизонтальную ось (рис 10.1). Под действием силы тяжести диск опускается, и нити разматываются до полной длины. В нижнем положении раскрутившийся маховичок продолжает вращение в том же направлении и наматывает нить на ось. Дойдя до верхней точки, диск останавливается и снова начинает свое движение, совершая таким образом колебания по вертикальной прямой линии; поэтому такое устройство и называется маятником.

Напомним, что для описания движения ось моментов выбираем жестко связанную с маятником и проходящую через его центр тяжести. Но такая система отсчета при ускоренном движении маятника будет неинерциальной. В ней будут действовать силы инерции и при составлении уравнения моментов (10.2) должны быть учтены в правой части уравнения моменты сил инерции. Однако, для плоского движения твердого тела можно выбрать ось, связанную с телом, относительно которой моменты сил инерции оказываются равными нулю, и поэтому уравнение моментов имеет такой же вид, как и для осей, неподвижных в пространстве. Этим свойством обладает ось, движущаяся поступательно (т.е. перпендикулярно к плоскостям, в которых движутся точки тела) и проходящая через центр тяжести тела. Тогда равнодействующая сил инерции, так же как и равнодействующая сил тяжести, будет приложена к центру тяжести тела и момент ее относительно оси, проходящей через центр тяжести, будет равен нулю.

В нашем случае этой осью будет геометрическая ось диска. Так как эта ось неподвижна относительно диска, можно написать выражение момента импульса относительно этой оси

(10.3)

где – момент инерции диска относительно этой же оси, – угловая скорость;

а уравнение моментов принимает вид:

, (10.4)

где – угловое ускорение диска.

Составим далее уравнения плоского движения диска. На диск массой действуют внешние силы: тяжести и натяжение нити . Момент силы тяжести относительно выбранной оси ( как и момент сил инерции) равен нулю. Поэтому уравнения (10.1) и (10.4) примут вид

, (10.5)

. (10.6)

Так как центр тяжести опускается как раз на столько, на сколько раскручивается нить, то величина перемещения центра тяжести диска и угол поворота его связаны соотношением .

Дифференцируя это соотношение дважды по времени, найдем связь между ускорением центра масс и угловым ускорением диска:

и . (10.7)

Решая систему уравнений (10.5), (10.6) и (10.7), находим ускорение

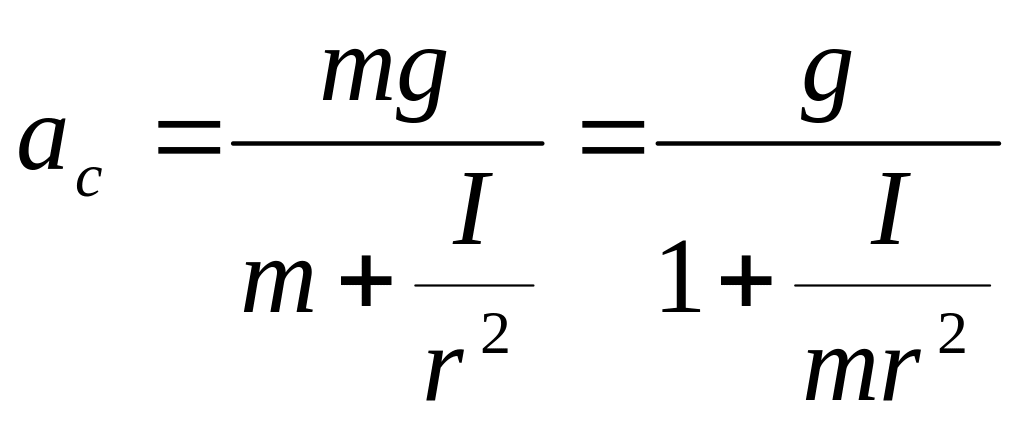(10.8)

и силу натяжения нити

(10.9)

Из формул (10.8),(10.9) следует, что ускорение и сила натяжения нити не зависят от того, в каком направлении движется маятник  вверх или вниз. Следовательно, вес движущегося маятника не зависит от направления движения маховичка и оказывается меньше веса маятника в состоянии покоя. (Сравните движение маятника Максвелла с равноускоренным движением по вертикальной прямой линии груза, подвешенного на нити.)

Из уравнения (10.8) находим момент инерции маятника:

Ускорение находится по измеренному времени движения и пройденному пути:

.

Итак, момент инерции маятника:

. (10.10)

Поскольку силы трения не принимаются во внимание, то формулу для момента инерции маховика можно получить также из закона сохранения механической энергии. Для двух крайних положений диска:

или .

Отсюда

.