Теоретическое введение

Кинематические характеристики вращательного движения.

Движение твердого тела, при котором все точки прямой, жестко связанной с телом, остаются неподвижными, называется вращением тела вокруг неподвижной оси. Прямая называется осью вращения.

При вращении тела вокруг закрепленной оси все его точки описывают окружности различного радиуса и, следовательно, имеют различные перемещения, скорости и ускорения. Тем не менее можно описать вращательное движение всех точек тела одинаковым образом. Для этого используют следующие кинематические характеристики движения: угол поворота , угловую скорость и угловое ускорение . Роль перемещения при вращательном движении играет вектор малого поворота (угловое перемещение) вокруг оси вращения. Он будет одинаков для любой точки абсолютно твердого тела, то есть тела, деформациями которого можно пренебречь. Модуль вектора поворота равен величине угла поворота Δφ, вектор поворота направлен по оси вращения по правилу буравчика (правого винта).

Характеристикой быстроты вращения служит угловая скорость тела, равная отношению вектора элементарного угла поворота тела к продолжительности этого поворота:

. (8.1)

Вектор угловой скорости направлен по оси вращения так же, как и угловое перемещение.

Быстроту изменения угловой скорости во времени характеризует угловое ускорение

. (8.2)

При возрастании угловой скорости ω угловое ускорение совпадает с ней по направлению, при убывании – направлено в противоположную сторону.

Найдем связь между линейными и угловыми величинами. Величина линейного перемещения точки, вращающейся по окружности радиуса :

. (8.3)

Разделив обе части уравнения (8.3) на , получим: . Так как производная пути по времени – это величина скорости: , а (8.1), то:

. (8.4)

Теперь продифференцируем (8.4) по времени: , или:

, (8.5)

где – касательное (тангенциальное) ускорение, определяющее быстроту изменения модуля скорости :

. (8.6)

Динамика твердого тела.

П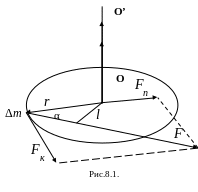 усть на тело действует сила . Моментом силы относительно точки О называется физическая величина, равная векторному произведению радиус-вектора , проведенного из точки О в точку приложения силы, на вектор силы :

. (8.7)

Направление момента силы определяется правилом буравчика (рис.8.1), величина момента силы

, (8.8)

где – угол между радиус-вектором точки приложения силы и вектором силы .

Момент силы относительно оси характеризует способность силы вращать тело вокруг этой оси. Составляющая силы, параллельная оси, вращения тела вызвать не может, а напряжения, возникающие в оси, нас не интересуют. Тогда достаточно рассмотреть силы, направления которых перпендикулярны оси вращения ОО’ (рис.8.1). Определим плечо силы относительно оси ОО’ как расстояние от оси вращения до линии действия силы, тогда

,

. (8.9)

Более того, поворот тела с закрепленной осью вращения может быть вызван только касательной составляющей силы , причем эта составляющая тем успешнее осуществит поворот, чем больше ее плечо r:

, (8.10)

так как .

Пусть твердое тело разбито на отдельные элементарные массы Δm. Выразим касательную составляющую равнодействующей сил, приложенных к этой точке, по второму закону Ньютона:

. (8.11)

Учитывая (8.5) для касательного ускорения, получим из (8.10) и (8.11):

. (8.12)

Скалярная величина

, (8.13)

равная произведению массы материальной точки на квадрат ее расстояния до оси, называется моментом инерции материальной точки относительно оси.

Векторы и совпадают по направлению с осью вращения, связаны с направлением вращения по правилу буравчика, поэтому равенство (8.12) можно переписать в векторной форме:

. (8.14)

Уравнение (8.14) является основным законом динамики вращательного движения для материальной точки. Соотношение, аналогичное (8.12), можно записать для каждой точки тела, и затем просуммировать по всем точкам, тогда (с учетом того, что угловое ускорение одинаково для всех точек и его можно вынести за знак суммы):

. (8.15)

В левой части равенства стоит сумма моментов всех сил (и внешних, и внутренних), приложенных к каждой точке тела. Но по третьему закону Ньютона, силы, с которыми точки тела взаимодействуют друг с другом (внутренние силы), равны по величине и противоположны по направлению и лежат на одной прямой, поэтому их моменты компенсируют друг друга. Таким образом, в левой части (8.15) остается суммарный момент только внешних сил.

Сумма произведений элементарных масс на квадрат их расстояний от оси вращения называется моментом инерции твердого тела относительно данной оси:

. (8.16)

Момент инерции твердого тела является мерой инертных свойств твердого тела при вращательном движении и аналогичен массе тела во втором законе Ньютона. Он существенно зависит не только от массы тела, но и от ее распределения относительно оси вращения (в направлении, перпендикулярном оси).

В случае непрерывного распределения массы сумма в (8.16) сводится к интегралу по всему объему тела:

. (8.17)

Таким образом, доказан основной закон динамики твердого тела: угловое ускорение твердого тела прямо пропорционально суммарному моменту внешних сил, приложенных к телу, и обратно пропорционально моменту инерции тела относительно оси вращения

. (8.18)

Этот закон аналогичен второму закону Ньютона при поступательном движении:

(8.19)

и позволяет определить угловое ускорение твердого тела.

Приведем моменты инерции для некоторых однородных тел.

1. Момент инерции тонкостенного кольца (обруча) радиуса R относительно оси, проходящей через его центр и перпендикулярной его плоскости:

. (8.20)

2. Момент инерции круглого диска (цилиндра) относительно оси, проходящей через его центр и перпендикулярной плоскости диска:

. (8.21)

3. Момент инерции однородного полого диска (толстостенного кольца) внутренним радиусом и внешним радиусом относительно оси, проходящей через центр масс перпендикулярно плоскости диска:

. (8.22)

4. Момент инерции шара относительно оси, проходящей через его центр:

. (8.23)

5. Момент инерции тонкого длинного стержня длиной l относительно оси, проходящей через его середину перпендикулярно стержню:

. (8.24)

Подсчет момента инерции тела относительно произвольной оси облегчается применением теоремы Штейнера: момент инерции тела относительно любой оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями

. (8.20)