ОГЛАВЛЕНИЕ

Предисловие
Занятие 1. Коллоквиум. Современные науки о космосе и Земле ………...............................…..
Практическая работа. Принцип возрастания энтропии ......…………….……...……
Занятие 2. Коллоквиум. Науки о сложных системах …….………………………….………….
Практическая работа. Принципы относительности ………………....….....……..
Занятие 3. Коллоквиум. История и современные достижения химии …………………….…...
Практическая работа. Микромир – мир элементарных частиц. Развитие представлений о строении Вселенной ……………….................................………...…...
Занятие 4. Коллоквиум. Достижения и концепции биологии …………………………....……..
Практическая работа. Мегамиры. Земля и Вселенная. Современные концепции развития геосферных оболочек …..........................................................……………….
Занятие 5. Коллоквиум. Современные науки о человеке ….........…………………………..…..
Практическая работа. Внутреннее строение и история геологического развития Земли. Литосфера как абиотическая основа жизни. Химические процессы.............…
Занятие 6. Практическая работа. Особенности биологического уровня описания материи. Многообразие живых организмов. Принципы эволюции. Генетика и эволюция. Происхождение человека .…….....................................................................................
Итоговое тестирования ……………………............……….....................................................…...
Вопросы к зачету ...............................................................................................................................

ПРЕДИСЛОВИЕ

Практикум создан для преподавания учебной дисциплины «Естественнонаучная картина мира» (базовой части Математического и естественнонаучного цикла) бакалаврам Мичуринского государственного педагогического института, обучающимся по профилям подготовки «Биология», «Химия» и «Безопасность жизнедеятельности» (направление подготовки 050100 Педагогическое образование).

Изучение дисциплины «Естественнонаучная картина мира» преследует цель ознакомления бакалавров с неотъемлемым компонентом единой культуры – естествознанием – и формирования у них целостного взгляда на окружающий мир. Курс задуман как междисциплинарное динамичное описание основных явлений, законов природы и тех научных открытий, которые послужили началом революционных изменений в технологиях, мировоззрении или общественном сознании.

Каждая тема включает вопросы к коллоквиуму, задания для выполнения практических работ, методическое обеспечение, представленное текстовыми, табличными и графическими приложениями, ссылки на литературные источники для самостоятельной подготовки к коллоквиуму.

В результате изучения курса «Естественнонаучная картина мира» студенты должны:

• овладеть понятийно-категориальным аппаратом естествознания, знаниями о структуре науки, ее методологии и истории формирования;

• узнать основополагающие концепции различных естественных наук, складывающихся в единую картину мира, закономерности развития научного знания, специфику гуманитарного и естественнонаучного компонентов культуры;

• иметь представление о естественнонаучной картине мира, о целостности и многообразии природы, о принципах преемственности, соответствия и непрерывности в изучении природы, а также о необходимости смены адекватного языка описания явлений по мере усложнения природных систем: от квантовой и статистической физики к химии и молекулярной биологии, от неживых систем к клетке, живым организмам, человеку, биосфере и обществу;

• понимать сущность жизни, принципы основных жизненных процессов организации биосферы, роли человечества в ее эволюции;

• иметь представление о смене типов научной рациональности, о революциях в естествознании и смене научных парадигм как ключевых этапах развития естествознания; о принципах универсального эволюционизма и синергетики как диалектических принципах развития в приложении к неживой и живой природе, человеку и обществу.

Учебно-методическое пособие «Естественнонаучная картина мира. Практикум» предназначено для студентов очных и заочных отделений. В связи с меньшим количеством аудиторных занятий на заочном отделении рекомендуется выполнять задания, отмеченные звездочкой.

ЗАНЯТИЕ 1

Практическая работа. Принцип возрастания энтропии

Коллоквиум. Современные науки о космосе и Земле

Задание 1.^* Изучите основные понятия термодинамики и принципы первого начала термодинамики (прил. 1).

Ответьте на следующие вопросы: 1. В каком случае в термодинамической системе наступает термодинамическое равновесие? 2. Какими параметрами можно описать состояние термодинамического равновесия? 3. Изобразите графически термодинамический процесс в подогреваемой системе, представляющей собой поршень, наполненный газом. Проследите за изменением объема (ось – ОХ) и давления (ось – ОY) газа в поршне? 4. Дайте определение обратимым и необратимым термодинамическим процессам. Приведите примеры. 5. Существуют ли обратимые процессы в природе? Почему? 6. Запишите выводы I начала термодинамики и общее выражение закона сохранения и превращения энергии в трактовке первого начала термодинамики. 7. Объясните причину, по которой невозможно создать вечный двигатель первого рода?

Письменно ответить на 3 и 6 вопросы.

Задание 2.^* Изучите основные принципы второго начала термодинамики (прил. 2).

Ответьте на следующие вопросы: 1. Объясните принцип необратимости термодинамических процессов. В чем причина необратимости подобных явлений? 2. Сформулируйте выводы II начала термодинамики. 3. Исходя из формулировок I и II начал термодинамики, скажите какое из них объясняет качественную и количественную стороны превращения энергии, а какое – направление превращения энергии? 4. Объясните причину, по которой невозможно создать вечный двигатель второго рода?

Письменно ответить на 2 вопрос.

Задание 3.^* Выясните смысл понятия «энтропия» (прил. 3).

Ответьте на следующие вопросы: 1. В каком разделе физики и при изучении каких систем впервые было сформировано понятие «энтропия»? 2. Укажите «энтропийную» формулировку второго начала термодинамики. 3. Что понимается под энтропией в термодинамике? Приведите математическое выражение энтропии. 4. Дать определение понятию «энтропия». Что обозначает энтропия в статистической физике, теории информации, химии и биологии?

Письменно ответить на 2 и 4 вопросы.

Задание 4.^* Докажите универсальность принципа возрастания энтропии (прил. 4).

Ответьте на следующие вопросы. 1. Что понимается под универсальностью в природе? Приведите примеры универсальных явлений. 2. Каким образом соотносятся два понятия: «энтропия» и «вероятность события»? Выразите эту связь математически. 3. Почему в системах, находящихся в наиболее вероятном состоянии, энтропия возрастает? 4. Укажите на рисунке сосуды с наибольшей энтропией (с наименьшей упорядоченностью молекул).

Письменно приведите доказательства универсальности принципа возрастания энтропии.

Приложение 1

Термодинамика – раздел физики, изучающий превращение энергии в различных процессах (тепловых, механических, электрических, магнитных и др.), обусловленное тепловым движением молекул. Современная термодинамика затрагивает широкий круг вопросов, представляющих интерес для всех естественных наук и для философии в целом. Термодинамика построена в основном на двух фундаментальных законах, называемых началами термодинамики. Первое начало описывает количественную и качественную стороны процессов превращения энергии; второе – начало позволяет судить о направлении этих процессов.

Термодинамическая система – макроскопическое тело (или группа тел), которому свойственны процессы, сопровождающиеся переходом теплоты в другие виды энергии и обратные процессы. Примером термодинамической системы может служить газ, заключенный в цилиндр под поршнем. Если на термодинамическую систему не оказывается никакого внешнего воздействия, через некоторое время эта система приходит в со­стояние, при котором в ней прекращаются всякие макроскопические изменения. Такое состояние называется термодинамическим равновесием. При термодинамическом равновесии состояние системы в целом может описываться следующими тремя параметрами: температурой (Т), давлением (р) и объемом (V). Переход системы из одного состояния (p₁, V₁, T₁) в другое (p₂, V₂, T₂) называется термодинамическим процессом.

Процесс перехода системы из состояния 1 в состояние 2 называется обратимым, если возможен процесс перехода системы из состояния 2 в 1, при котором система, пройдя последовательно, но в обратном порядке вернется в начальное состояние 1. В противном случае процесс называется необратимым. Примером обратимого процесса могло бы служить колебание маятника, если бы оно происходило и без трения: в течение одного периода колебания маятник возвратился бы в начальное положение, причем ни в окружающей среде, ни в системе (маятнике) не произошло бы никаких изменений. Итак, обратимые процессы – понятие идеализированное. В природе обратимых процессов не существует.

Перейдем теперь к рассмотрению первого начала термодинамики, которое было сформулировано в сер. ХIХ в. в результате работ Ю. Майера, Дж. Джоуля и Г. Гельмгольца. Допустим, что некоторая система (например, газ, заключенный в цилиндр под поршнем), обладающая внутренней энергией (U₁) получила количество теплоты (Q) и, перейдя в новое состояние, характеризующее­ся внутренней энергией (U₂), совершила внешнюю работу (А). При этом изменение внутренней энергии системы будет равным:

U₂ – U₁ = Q – А, или Q = (U₂ – U₁) + А, или Q = ∆U + А.

Эта формула и есть математическое выражение первого начала термодинамики. Первое начало утверждает, что все количество теплоты, переданное системе, идет на изменение внутренней энергии системы и на совершаемую системой работу. Из первого начала термодинамики следует вывод: будучи несозидаемой и неуничтожимой, энергия может только переходить из одной формы в другую (видоизменяться), но не может возникать или исчезать. В такой формулировке первое начало термодинамики представляет собой общее выражение закона сохранения и превращения энергии.

Если система периодически возвращается в исходное состояние, то изменение ее внутренней энергии ∆U = 0. Тогда, согласно первому началу термодинамики, A = Q. Это означает, что невозможно создать периодически действующий механизм, который совершал бы работу, превышающую получаемую им энергию. Воображаемый механизм, совершающий работу, большую получаемой энергии, называется вечным двигателем первого рода.

Приложение 2

Второе начало термодинамики (ВНТ) устанавливает необратимость макроскопических процессов, протекающих с разностью температур. Процессы, связанные с теплообменом при конечной разности температур и сопровождающиеся трением, диффузией газов, расширением газов, выделением джоулевой теплоты и т.д., необратимы, т.е. могут самопроизвольно протекать только в одном направлении.

Исторически второе начало термодинамики возникло из анализа работы тепловых машин (С. Карно, 1824). Существует несколько эквивалентных формулировок ВНТ. Само название «ВНТ» и первая его формулировка принадлежат Р. Клаузиусу (1850): невозможен процесс, при котором теплота переходила бы самопроизвольно от тел более холодных к телам более нагретым. Этот процесс невозможно осуществить и при помощи приборов без того, чтобы в природе не произошли еще какие-либо изменения (механические, тепловые и т.д.). Другая формулировка ВНТ гласит: невозможен механизм, который все получаемое от нагревателя количество теплоты целиком переводил бы в работу; часть этого количества теплоты должна быть отдана холодильнику.

Если бы в нарушение положения Р. Клаузиуса переход теплоты от более холодных тел к более теплым оказался возможным, то можно было бы, разделив один тепловой резервуар на 2 части и переводя теплоту из одной в другую, получить 2 резервуара с различными температурами. Это позволило бы получить механическую работу с помощью периодически действующей (т.е. многократно возвращающейся к исходному состоянию) машины за счёт разницы температур между этими резервуарами. Воображаемый механизм, превращающий все количество теплоты в работу, называется вечным двигателем второго рода. Так, работа двигателя корабля за счёт охлаждения забортной воды океана – доступного и практически неисчерпаемого ресурса внутренней энергии – не противоречит закону сохранения энергии, но если, кроме охлаждения воды, нигде других изменений нет, то работа такого двигателя противоречит ВНТ. В реальном тепловом двигателе процесс превращения теплоты в работу обязательно сопряжён с передачей определённого количества теплоты внешней среде. В результате тепловой резервуар двигателя охлаждается, а более холодная внешняя среда нагревается, что находится в согласии со ВНТ. Следовательно, ВНТ можно формулировать и как невозможность создания вечного двигателя 2-го рода.

Приложение 3

Одна из формулировок второго начала термодинамики гласит: «Энтропия изолированной системы при проте­кании необратимых процессов возрастает, ибо систе­ма, предоставленная самой себе, переходит из менее вероятного состояния в более вероятное. Энтропия системы, находящейся в равновесном состоянии, мак­симальна и постоянна (∆S > 0)».

Энтропия (от греч. entropia – поворот, превращение) – понятие, впервые введенное в термодинамике (Р. Клаузиус, 1865) для определения меры необратимого рассеяния энергии неравновесной термодинамической системы.

В термодинамике энтропия (dS) – мера способности теплоты к превращению. В обратимых системах энтропия неизменна и представляет собой функцию состояния термодинамической системы, изменение которой в равновесном процессе равно отношению количества теплоты, сообщенного системе или отведенного от нее (δQ), к термодинамической температуре системы (T) : dS = δQ/T. В статистической физике энтропия – мера вероятности пребывания системы в данном состоянии (принцип Больцмана), в теории информации – мера неопределенности какого-либо опыта (испытания). Понятие «энтропия» используется также в химии, биологии и других областях науки как мера неупорядоченности, хаотичности.

Приложение 4

Любые замкнутые системы стремятся к равновесию. При этом процессы, стремящиеся привести систему к равновесному состоянию, согласно второму началу термодинамики, осиливают энтропию. В равновесном состоянии энтропия системы максимальна. Отсюда получаем вывод, что возрастание энтропии в изолированных системах, является универсальным принципом естествознания.

Чтобы убедиться в том, что энтропия действительно является мерой неупорядоченности, сопоставим понятия «энтропия» и «вероятность события» на следующем примере. Разделим сосуд на две равные части (рисунок). Пусть в нем находится только одна молекула. Двигаясь хаотически, она может оказаться как в левой, так и в правой части сосуда, причем оба случая одинаково возможны, или, как говорят, равновероятны. Вероятность события характеризуется отношением числа случаев осуществляющих данное событие, к числу всех возможных случаев. Очевидно, что вероятности случая, когда правая часть сосуда оказывается пустой, и случая, когда в ней находится молекула, одинаковы и равны 1/2. Поместим теперь в сосуд две молекулы, предварительно пронумеровав их. Тогда число возможных случаев размещения молекул по частям сосуда станет равным 4 = 2², а вероятность каждого случая 1/4 = 1/2². Если в сосуде будут находиться три пронумерованных молекулы, то число случаев размещения возрастет до 8 = 2³, а вероятность каждого случая уменьшится до 1/8 = 1/2³. При наличии в сосуде 4 молекул число случаев окажется равным 16 = 2⁴, а вероятность каждого случая уменьшится до 1/16 = 1/2⁴. Нетрудно сообразить, что при наличии в сосуде N молекул число случаев размещения этих молекул станет равным 2^N, а вероятность каждого случая l/2 ^N. Таким образом, по мере увеличения числа молекул вероятность каждого случая индивидуального размещения молекул уменьшается.

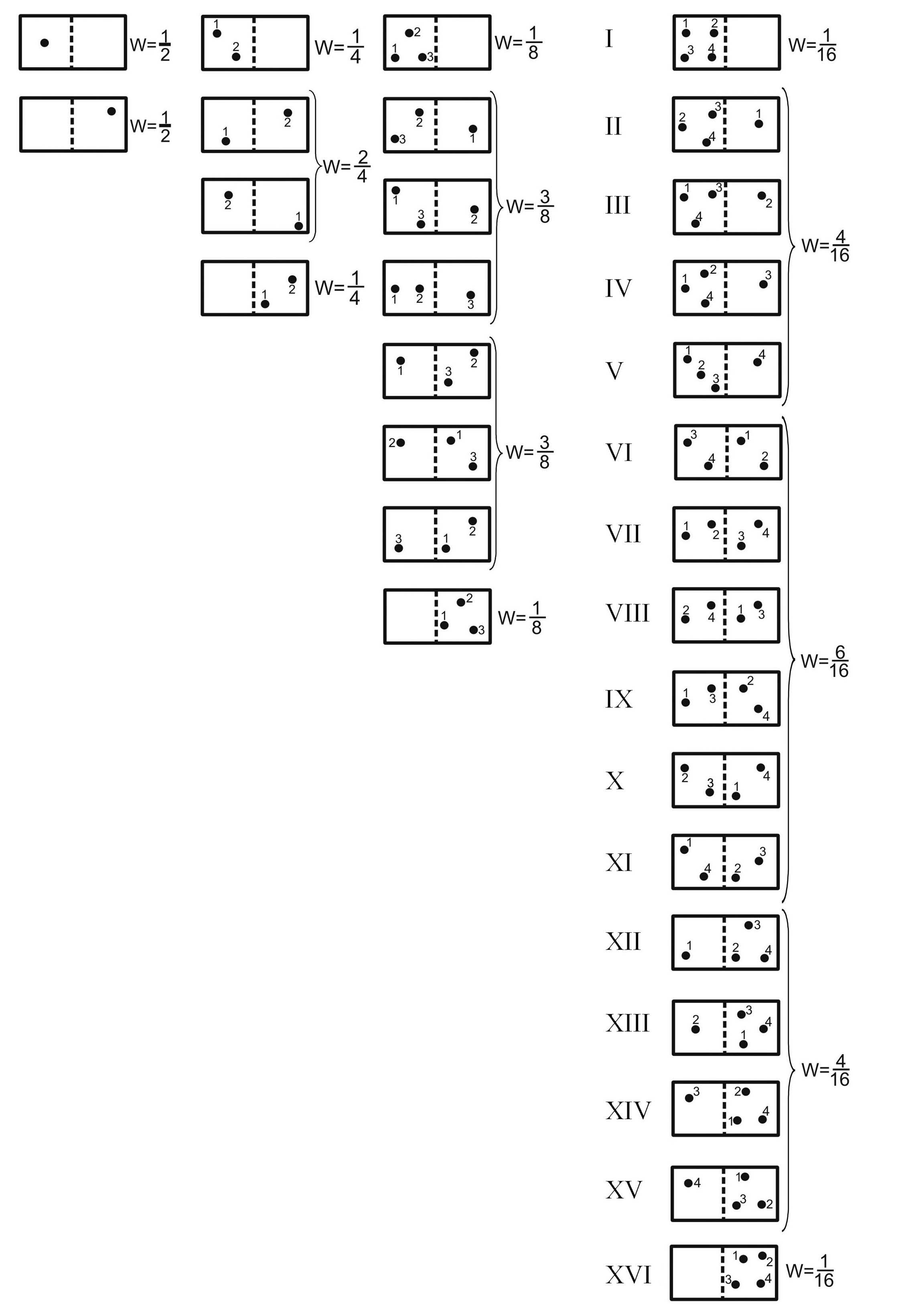
Рис. 1. Вероятность распределения молекул в сосуде

Учтем теперь, что на практике проследить за каждой молекулой невозможно. Кроме того, макроскопическое состояние системы не изменится, если, например, молекула 2, находя­щаяся в левой части сосуда, поменяется местом с молекулой 4, находящейся в правой его части (рис. 1). С этой точки зрения, случаи VI – XI тождественны: все они соответствуют одному состоянию системы (газа) – равномерному распределению молекул по объему сосуда. Вероятность этого состояния W = 6/16, т.к. оно может осуществляться шестью способа­ми. Точно так же случаи II – V являются тождественными и соответствуют дру­гому состоянию системы, вероятность которого W = 4/16, т.к. оно может осуществляться четырьмя способами. Тождественные случаи XII – XV соот­ветствуют третьему состоянию системы, вероятность которого W = 4/16. Чет­вертое состояние (случай I) осуществляется только одним единственным спо­собом; его вероятность W = 1/16. Такова же вероятность пятого состояния (слу­чай XVI).

Таким образом, система из четырех молекул может находиться в пяти раз­личных состояниях. Причем из всех этих состояний наиболее вероятным явля­ется равномерное распределение молекул по объему сосуда. Назовем такое состоя­ние равновесным. С увеличением числа молекул вероятность равновесного состояния будет все более и более возрастать по сравнению с вероятностью любого неравновес­ного состояния. При этом равномерное распределение молекул по объему является вместе с тем и наиболее беспорядочным их распределением. В этом смысле можно сказать, что вероятность состояния есть мера беспорядка состояния системы. Очевидно, что предоставленная самой себе изолиро­ванная система должна перейти в наиболее вероятное, т.е. равновесное состояние. Всякое отклонение от равно­весного состояния влечет за собой уменьшение вероятности состояния; очень неравновесные состояния являются пра­ктически неосуществимыми, хотя в принципе они возмо­жны.

Теперь вспомним последнюю формулировку второго начала термодинамики, в котором говорится о возрастании энтропии при переходе изолированных систем в равновесное состояние. Таким образом, при переходе системы в равновесное состояние она стремится перейти в наиболее статистически вероятное (наименее упорядоченное) состояние, при этом значение энтропии возрастает. Возрастание энтропии, стремление системы прейти в наиболее вероятное состояние (равновесное, но мало упорядоченное положение) оказываются взаимосвязанными категориями. Согласно исследованиям Больцмана, эта связь выражается формулой^*: S = k · lnW, где k – постоянная Больцмана, S – энтропия, lnW – натуральный логарифм вероятности состояния. Согласно этой формуле, все физические процессы протекают в направлении постепенного перехода от упорядоченного состояния к неупорядоченному, от состояния с меньшей вероятностью к состоянию с большей вероятностью.