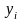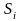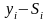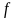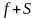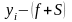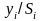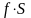Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Елецкий государственный университет им. И.А. Бунина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Posobie_Ekonometrika_Tinyakova.docx

Скачиваний:

Добавлен:

01.04.2025

Размер:

2.09 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 2514 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

4.1. Моделирование сезонных колебаний

4.1.1. Расчетные формулы

4.1.1.1. Модель с аддитивной сезонной составляющей

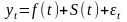где 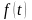– тренд; 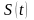– сезонная составляющая; 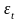– случайная компонента.

4.1.1.2. Модель с мультипликативной сезонной составляющей:

4.1.1.3. Модель временного ряда с циклическими колебаниями периодичностью k:

где .

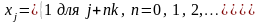4.2.2. Решение типовых задач

Задание 4.2.2.1. Некий предприниматель, оптовый поставщик фруктов на рынки г. Воронежа, желает спланировать свою деятельность на 2004г. таким образом, чтобы получить максимум прибыли. Большую часть в общем объеме его продаж занимают груши. Данные по этому виду фруктов представлены в табл. 4.2.2.1. Для того чтобы получить прогнозные оценки объема продаж груш на требуемый период, ему посоветовали построить модель с аддитивной сезонной компонентой.

Решение с помощью Excel

1. Ввод исходных данных и оформление их в виде таблицы, удобной для расчета оценок сезонной компоненты.

Т а б л и ц а 4.2.2.1

Год	Сезон	Объем продаж, т.	Год	Сезон	Объем продаж, т.
2000	зима	3836	2002	зима	5007
	весна	1831		весна	2096
	лето	11588		лето	14744
	осень	30945		осень	39328
2001	зима	4447	2003	зима	5437
	весна	2067		весна	2358
	лето	12938		лето	16644
	осень	34892		осень	44381

2. Расчет оценок сезонной компоненты для аддитивной модели.

2.1. Расчет скользящих средних с периодом усреднения, равным четырем.

2.2. Расчет центрированных скользящих средних, определяемых как полусумма двух соседних сглаженных наблюдений с целью приведения сглаженных значений в соответствии с фактическими моментами времени.

2.3. Вычисление сезонной компоненты в виде разницы фактических значений и центрированных скользящих средних.

2.4. Оформление результатов расчетов в виде табл. 4.2.2.2.

Т а б л и ц а 4.2.2.2

Год	Сезон	Объем продаж	Скользящее среднее за 4 периода	Центрированное скользящее среднее	Оценка сезонной компоненты
Год	Сезон	Объем продаж	Скользящее среднее за 4 периода	Центрированное скользящее среднее	Оценка сезонной компоненты
2000	зима	3836	-	-	-
	весна	1831	12050,22	-	-
	лето	11588	12202,94	12126,58	-538,48
	осень	30945	12261,76	12232,35	18713,00
2001	зима	4447	12599,16	12430,46	-7983,58
	весна	2067	13585,73	13092,45	-11025,72
	лето	12938	13725,87	13655,80	-718,14
	осень	34892	13733,26	13729,57	21162,10
2002	зима	5007	14184,86	13959,06	-8951,61
	весна	2096	15293,95	14739,40	-12643,15
	лето	14744	15401,30	15347,62	-603,56
	осень	39328	15466,75	15434,03	23894,00
2003	зима	5437	15941,81	15704,28	-10267,41
	весна	2358	17205,05	16573,43	-14215,40
	лето	16644	-	-	-
	осень	44381	-	-	-

3. Расчет средних значений сезонной компоненты аддитивной модели.

3.1. Формирование из оценок сезонной компоненты, полученных в предыдущем пункте, табл. 4.2.2.3, удобной для расчета средних значений этой же компоненты.

3.2. Расчет итоговых значений сезонной компоненты.

3.3. Определение средних значений итоговой компоненты.

Т а б л и ц а 4.2.2.3

Показатели	Год	Сезон
Показатели	Год	Зима	Весна	Лето	Осень
	2000	-	-	-538,48	18713,00
	2001	-7983,58	-11025,72	-718,14	21162,10
	2002	-8951,61	-12643,15	-603,56	23894,00
	2003	-10267,41	-14215,40	-	-
Итого за сезон		-27202,59	-37884,28	-1321,69	45056,09
Средняя оценка сезонной компоненты		-9067,53	-12628,09	-440,56	15018,70
Скорректированная сезонная компонента		-7288,16	-10848,72	1338,81	16798,07

3.4. Определение корректирующего коэффициента

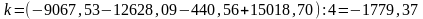3.5. Расчет скорректированных значений сезонной компоненты путем вычитания корректирующего коэффициента из средних оценок сезонной компоненты (сумма скорректированных значений равна 0).

4. Вычисление основных составляющих сезонной модели ( ).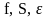

4.1. Элиминирование влияния сезонной компоненты путем вычитания ее значения из каждого уровня исходного временного ряда.

4.2. Построение по данным элиминированного временного ряда трендовой модели с помощью МНК. Оформление результатов моделирования в виде табл. 4.2.2.4.

Т а б л и ц а 4.2.2.4

Результаты моделирования
Коэффициент регрессии	554,41
Стандартная ошибка	209,77
Множественный R	0,58
Константа	9821,28
Число наблюдений	16
Число степеней свободы	14
F - критерий	6,99

4.3. Получение расчетных значений по трендовой модели.

4.4. Расчет значений уровня ряда по аддитивной модели.

4.5. Вычисление отклонений расчетных значений от фактических.

4.6. Оформление результатов расчетов в виде табл. 4.2.2.5.

Т а б л и ц а 4.2.2.5

Год	Сезон
2000	зима	3835,98	-7288,16	11124,14	10375,68	3087,53	748,46
	весна	1831,44	-10848,72	12680,16	10930,09	81,37	1750,07
	лето	11588,10	1338,81	10249,29	11484,50	12823,31	-1235,21
	осень	30945,35	16798,07	14147,28	12038,91	28836,98	2108,38
2001	зима	4446,88	-7288,16	11735,04	12593,31	5305,15	-858,27
	весна	2066,72	-10848,72	12915,44	13147,72	2299,00	-232,28
	лето	12937,67	1338,81	11598,86	13702,13	15040,94	-2103,27
	осень	34891,66	16798,07	18093,59	14256,53	31054,60	3837,06
2002	зима	5007,45	-7288,16	12295,60	14810,94	7522,78	-2515,34
	весна	2096,25	-10848,72	12944,97	15365,35	4516,63	-2420,38
	лето	14744,07	1338,81	13405,26	15919,76	17258,57	-2514,50
	осень	39328,02	16798,07	22529,95	16474,16	33272,23	6055,79
2003	зима	5436,87	-7288,16	12725,03	17028,57	9740,41	-4303,54
	весна	2358,03	-10848,72	13206,75	17582,98	6734,26	-4376,23
	лето	16644,32	1338,81	15305,51	18137,39	19476,19	-2831,87
	осень	44380,99	16798,07	27582,92	18691,79	35489,86	8891,13

5. Построение с помощью «Мастера диаграмм» графика (рис. 4.2.2.1), отражающего динамику объема продаж груш на рынках г. Воронежа (фактических, рассчитанных по трендовой и аддитивной моделям).

6. Расчет прогнозных значений для каждого сезонного периода 2004г.

;

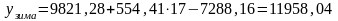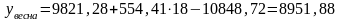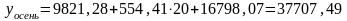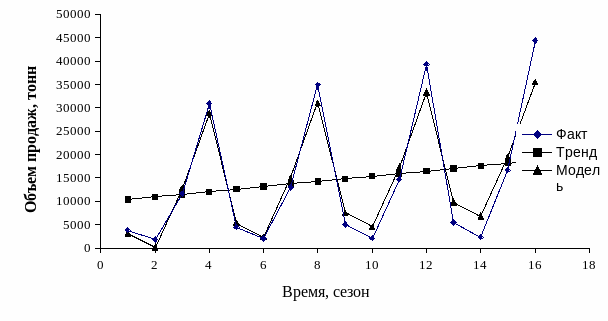
Р и с. 4.2.2.1. Динамика фактического и расчетных объемов продаж груш, т.

Задание 4.2.2.2. Известно, что стоимость репетиторских услуг зависит от спроса на такие услуги, который распределен по периодам подготовки к вступительным экзаменам. Условно можно выделить четыре периода: 1) август –октябрь (низкая стоимость); 2) ноябрь – декабрь (средняя стоимость); 3) январь – март (стоимость выше средней); апрель – июль (высокая стоимость). Усредненные значения стоимости репетиторских услуг в г. Воронеже за четыре года с разбивкой по периодам приведены в табл. 4.2.2.6. Абитуриенты решили построить модель сезонных колебаний для расчета ожидаемой стоимости репетиторских услуг в 2004 г.

Таблица 4.2.2.6

Год	Период	Цена занятие, руб.	Год	Период	Цена занятия, руб.
2000	1	65	2002	1	145
	2	95		2	190
	3	140		3	250
	4	190		4	310
2001	1	110	2003	1	175
	2	155		2	240
	3	185		3	310
	4	250		4	375

Решение с помощью Excel

1. Ввод исходных данных и оформление их в виде таблицы, удобной для расчета оценок сезонной компоненты.

2. Построение графика временного ряда, характеризующего стоимость репетиторских услуг (см. рис. 4.2.2.2).

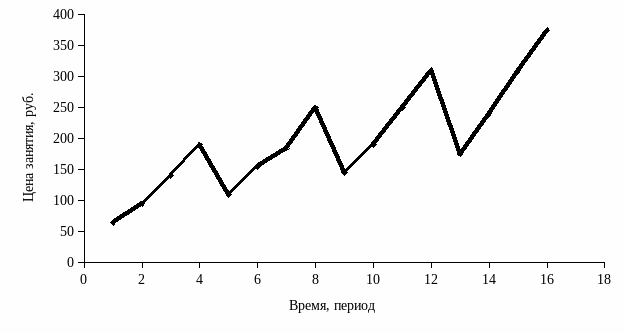
Р и с. 4.2.2.2. Динамика стоимости репетиторских услуг

Построенный график свидетельствует о наличии сезонных колебаний с периодом, равным четырем, с общей тенденцией роста стоимости репетиторских услуг и увеличением амплитуды колебаний. Поскольку амплитуда сезонных колебаний увеличивается, то целесообразно для данного ряда строить мультипликативную модель.

3. Расчет оценок сезонной компоненты для мультипликативной модели.

3.1. Расчет скользящих средних с периодом усреднения, равным четырем.

3.2. Расчет центрированных скользящих средних, определяемых как полусумма двух соседних сглаженных наблюдений с целью приведения сглаженных значений в соответствие с фактическими моментами времени.

3.3. Вычисление сезонной компоненты в виде частного от деления фактических уровней временного ряда на значения центрированных скользящих средних.

3.4. Оформление результатов расчетов в виде табл. 4.2.2.7.

4. Расчет средних значений сезонной компоненты мультипликативной модели.

4.1. Формирование из оценок сезонной компоненты, полученных в предыдущем пункте, табл. 4.2.2.8, удобной для расчета средних значений этой же компоненты.

4.2. Расчет итоговых значений сезонной компоненты.

4.3. Определение средних значений итоговой компоненты.

Т а б л и ц а 4.2.2.7

Год	Период	Цена занятия, руб.	Скользящее среднее за 4 периода	Центрированное скользящее среднее	Оценка сезонной компоненты
Год	Период	Цена занятия, руб.	Скользящее среднее за 4 периода	Центрированное скользящее среднее	Оценка сезонной компоненты
2000	1	65	-	-	-
	2	95	122,50	-	-
	3	140	133,75	128,13	1,09
	4	190	148,75	141,25	1,35
2001	1	110	160,00	154,38	0,71
	2	155	175,00	167,50	0,93
	3	185	183,75	179,38	1,03
	4	250	192,50	188,13	1,33
2002	1	145	208,75	200,63	0,72
	2	190	223,75	216,25	0,88
	3	250	231,25	227,50	1,10
	4	310	243,75	237,50	1,31
2003	1	175	258,75	251,25	0,70
	2	240	275,00	266,88	0,90
	3	310	-	-	-
	4	375	-	-	-

Т а б л и ц а 4.2.2.8

Показатели	Год	Период
Показатели	Год	1	2	3	4
	2000	-	-	1,09	1,35
	2001	0,71	0,93	1,03	1,33
	2002	0,72	0,88	1,10	1,31
	2003	0,70	0,90	-	-
Итого за период		2,13	2,70	3,22	3,98
Средняя оценка сезонной компоненты		0,710	0,901	1,074	1,326
Скорректированная сезонная компонента		0,708	0,898	1,070	1,322

4.4. Определение корректирующего коэффициента.

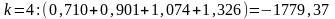4.5. Расчет скорректированных значений сезонной компоненты путем умножения корректирующего коэффициента из средних оценок сезонной компоненты (сумма скорректированных значений равна четырем).

5. Вычисление основных составляющих сезонной модели ( ).

5.1. Элиминирование влияния сезонной компоненты путем деления каждого уровня исходного временного ряда на соответствующие значения сезонной составляющей.

5.2. Построение по данным элиминированного временного ряда трендовой модели с помощью МНК. Оформление результатов моделирования в виде табл. 4.2.2.9.

Т а б л и ц а 4.2.2.9

Результаты моделирования
Константа	87,21
Коэффициент регрессии	12,78
Стандартная ошибка	0,35
Множественный R	0,99
Число наблюдений	16
Число степеней свободы	14
F - критерий	1326,21

5.3. Получение расчетных значений по трендовой модели.

5.4. Расчет значений уровня ряда по мультипликативной модели.

5.5. Вычисление отклонений расчетных значений от фактических.

5.6. Оформление результатов расчетов в виде табл. 4.2.2.10.

Т а б л и ц а 4.2.2.10

Год	Период
2000	1	65	0,71	91,76	99,99	70,83	0,92	-5,83
	2	95	0,90	105,76	112,77	101,30	0,94	-6,30
	3	140	1,07	130,72	125,54	134,45	1,04	5,55
	4	190	1,32	143,69	138,32	182,90	1,04	7,10
2001	1	110	0,71	155,28	151,09	107,03	1,03	2,97
	2	155	0,90	172,55	163,87	147,20	1,05	7,80
	3	185	1,07	172,74	176,64	189,18	0,98	-4,18
	4	250	1,32	189,06	189,42	250,47	1,00	-0,47
2002	1	145	0,71	204,69	202,19	143,23	1,01	1,77
	2	190	0,90	211,51	214,97	193,10	0,98	-3,10
	3	250	1,07	233,43	227,74	243,91	1,02	6,09
	4	310	1,32	234,44	240,52	318,04	0,97	-8,04
2003	1	175	0,71	247,04	253,29	179,43	0,98	-4,43
	2	240	0,90	267,17	266,07	239,01	1,00	0,99
	3	310	1,07	289,45	278,84	298,64	1,04	11,36
	4	375	1,32	283,59	291,62	385,61	0,97	-10,61

6. Построение графика (см. рис. 4.2.2.3) стоимости репетиторских услуг в г. Воронеже (фактических, рассчитанных по трендовой и мультипликативной моделям).

7. Расчет прогнозных значений для каждого сезонного периода 2004г.:

; ;

; .

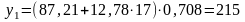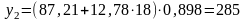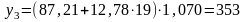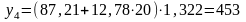Задание 4.2.2.3. Аграрный комитет администрации Воронежской области, зная среднегодовой спрос на молоко населения области, заинтересован в получении прогнозных оценок производства этого продукта хозяйствами всех категорий на следующий год. Такая информация ему необходима для того, чтобы иметь представление о степени обеспеченности населения молочной продукцией, и в случае существенного превышения спроса над предложением молока ориентировать торговые организации на заключение договоров поставки молока с производителями из других регионов. Построение прогнозной модели решено осуществить по данным табл. 4.2.2.11.

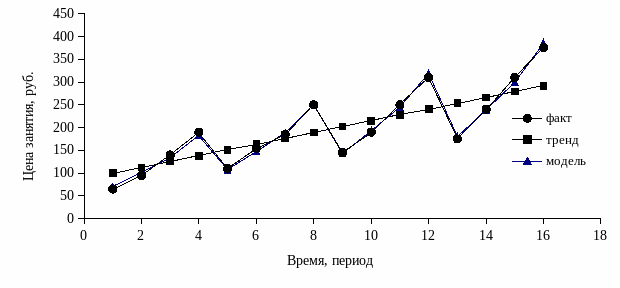
Р и с. 4.2.2.3. Динамика фактической и расчетной стоимости репетиторских услуг

Т а б л и ц а 4.2.2.11

Год	Производство молока в хозяйствах всех категорий Воронежской обл., т.
Год	1-й квартал	2-й квартал	3-й квартал	4-й квартал
1998	6112	11446	11110	5468
1999	6090	11249	10666	5250
2000	5846	10784	10347	5297
2001	5864	10652	10329	5432
2002	5944	10856	10487	5618
2003	6095	10922	10725	5763

Решение с помощью Excel

Ввод исходных данных и оформление их в удобном для проведения расчетов виде.
Формирование фиктивных переменных :

;

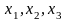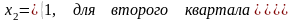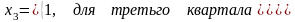и оформление полученных результатов в виде табл. 4.2.2.12.

3. Оценка параметров модели

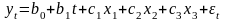обычным МНК с помощью «Пакета анализа» (см. Вывод итогов 4.2.2.1).

Т а б л и ц а 4.2.2.12


1	1	0	0	6112	13	1	0	0	5864
2	0	1	0	11446	14	0	1	0	10652
3	0	0	1	11110	15	0	0	1	10329
4	0	0	0	5468	16	0	0	0	5432
5	1	0	0	6090	17	1	0	0	5944
6	0	1	0	11249	18	0	1	0	10856
7	0	0	1	10666	19	0	0	1	10487
8	0	0	0	5250	20	0	0	0	5618
9	1	0	0	5846	21	1	0	0	6095
10	0	1	0	10784	22	0	1	0	10922
11	0	0	1	10347	23	0	0	1	10725
12	0	0	0	5297	24	0	0	0	5763

ВЫВОД ИТОГОВ 4.2.2.1

Регрессионная статистика
Множественный R	0,996532
R-квадрат	0,993076
Нормированный R-квадрат	0,991618
Стандартная ошибка	238,7258
Наблюдения	24

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	4	1,55E+08	38823023	681,225	3,18E-20
Остаток	19	1082810	56990,02
Итого	23	1,56E+08

	Коэффи-циенты	Стандартная ошибка	t-статис-тика	P-Значе-ние	Нижние 95%	Верхние 95%
Y-пересечение	5576,383	139,5406	39,96243	8,46E-20	5284,321	5868,445
Переменная X 1	-7,50357	7,133298	-1,05191	0,306037	-22,4337	7,426598
Переменная X 2	497,9893	139,4798	3,570331	0,002042	206,0545	789,9241
Переменная X 3	5498,493	138,5648	39,68174	9,65E-20	5208,473	5788,512
Переменная X 4	5131,83	138,0129	37,1837	3,27E-19	4842,965	5420,694

Таким образом, построенная модель имеет вид

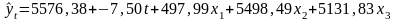Коэффициент корреляции достаточно высокий, что свидетельствует о существовании тесной взаимосвязи объема молока от соответствующих факторов.

Сравнение с табличным значением дисперсионного отношения Фишера 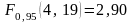позволяет сделать вывод об адекватности построенной модели.

Сравнение расчетных значений -статистик с табличным значением говорит о том, что включенные в модель факторы значимы, кроме фактора времени. Таким образом, тенденция уменьшения объема молока существует, но она статистически незначима на 95%-ом уровне значимости. Поэтому необходимо перестроить модель, исключив из нее незначимый фактор.

4. Оценка параметров модели

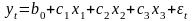обычным МНК с помощью «Пакета анализа» (см. Вывод итогов 4.2.2.2)

ВЫВОД ИТОГОВ 4.2.2.2

Регрессионная статистика
Множественный R	0,996329
R-квадрат	0,992672
Нормированный R-квадрат	0,991573
Стандартная ошибка	239,3606
Наблюдения	24

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	3	1,55E+08	51743010	903,1216	1,65E-21
Остаток	20	1145870	57293,52
Итого	23	1,56E+08

	Коэффи-циенты	Стандартная ошибка	t-статис-тика	P-Зна-чение	Нижние 95%	Верхние 95%
Y-пересечение	5471,333	97,71857	55,99072	1,85E-23	5267,496	5675,171
Переменная X 1	520,5	138,1949	3,766419	0,001214	232,2306	808,7694
Переменная X 2	5513,5	138,1949	39,89654	1,53E-20	5225,231	5801,769
Переменная X 3	5139,333	138,1949	37,18901	6,14E-20	4851,064	5427,603

Следовательно, построенная модель имеет вид

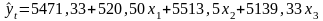Анализ этой модели позволяет сделать вывод о ее пригодности для целей прогнозирования.

5. Получение с помощью построенной модели прогнозных оценок производства молока на 2004 год и оформление результатов в виде табл. 4.2.2.13.

Т а б л и ц а 4.2.2.13

Год	Квартал
2004	1-й квартал	1	0	0	5991,83
	2-й квартал	0	1	0	10984,83
	3-й квартал	0	0	1	10610,67
	4-й квартал	0	0	0	5471,33

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 2514 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.02.2015210.43 Кб150OS.doc
#
09.11.2019412.16 Кб12OTChET_PROTEK_1.doc
#
22.04.2019326.96 Кб38OTVYeT_ZYeMLYa.docx
#
01.03.202528.52 Mб0Part 2.doc
#
27.04.2019385.02 Кб21PITANIYe.doc
#
01.04.20252.09 Mб0Posobie_Ekonometrika_Tinyakova.docx
#
05.09.2019885.76 Кб23posobie_po_ekonomike_1.doc
#
19.11.2018167.94 Кб20Poyasnitelnaya_zapiska (4).doc
#
01.05.2025165.41 Кб1praktika_otchet_1 (1).docx
#
01.05.2025569.79 Кб0praktika_otchet_1 (1).docx
#
09.02.2015100.86 Кб19praktika_TB_2013_1.doc